Информатика егэ 1 задание, объяснение и разбор
На уроке рассмотрено решение 1 задание ЕГЭ по информатике 2017: дается подробное объяснение и разбор заданий
Объяснение задания 1 ЕГЭ по информатике
1-я тема характеризуется, как задания базового уровня сложности,
время выполнения – примерно 1 минута,
максимальный балл — 1
«Перевод всех используемых в задании чисел в десятичную систему сам по себе не является ошибкой, но приводит к лишним вычислениям и увеличению вероятности арифметической ошибки»
ФГБНУ «Федеральный институт педагогических измерений»
Системы счисления и представление информации в памяти ПК
Для решения 1 задания следует вспомнить и повторить следующие темы:
Двоичная система счисления
Количество цифр или основание системы: 2
Цифры (алфавит): 0, 1
Перевод чисел из 10-й системы счисления в двоичную:
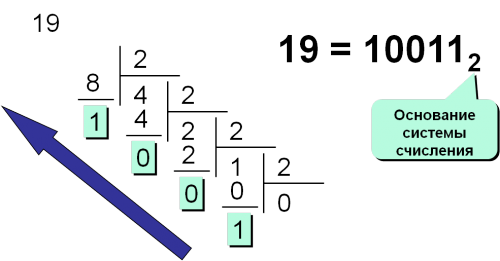
Перевод чисел из 10-й сист. сч-я в двоичную
Егифка ©:

Перевод чисел из 2-й системы счисления в 10-ую:
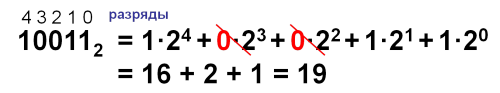
Перевод чисел из 2-й сист. сч-я в 10-ую
Егифка ©:

При работе с большими числами, лучше использовать разложение по степеням двойки:
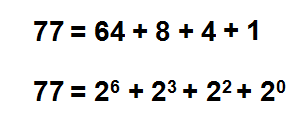
Разложение по степеням двойки
Егифка ©:

Восьмеричная система счисления
Количество цифр или основание системы: 8
Цифры (алфавит): 0, 1, 2, 3, 4, 5, 6, 7
Перевод чисел из 10-й системы счисления в 8-ую
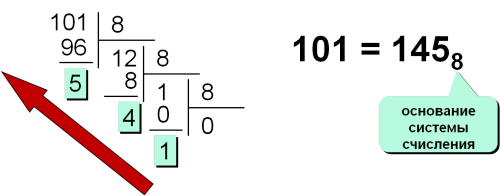
Перевод чисел из 10-й сист. сч-я в 8-ую
Перевод чисел из 8-й сист. сч-я в 10-ую

Перевод чисел из 8-й системы счисления в 10-ую
Перевод чисел из 8-й сист. сч-я в 2-ую и обратно триадами

Перевод из 8-й сист. сч-я в 2-ую и обратно триадами
Егифка ©:

Шестнадцатеричная система счисления
Количество цифр или основание системы: 16
Цифры (алфавит): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A (10), B (11), C (12), D (13), E (14), F (15)
Перевод чисел из 10-й системы счисления в 16-ую
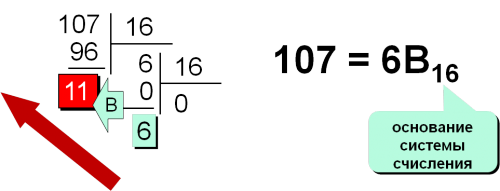
Перевод из 10-й сист. сч-я в 16-ую
Перевод из 16-й системы счисления в 10-ую

Перевод из 16-й сист. сч-я в 10-ую
Перевод чисел из 2-й сист. сч-я в 16-ую и обратно тетрадами

Перевод из 2-й с. сч-я в 16-ую и обратно тетрадами
Егифка ©:

Полезности для двоичной системы счисления:
26 = 64 ≤ 126 7, 126 = 11111102 (7 цифр)
32 = 25 = 1000002
31 = 25-1 = 111112
15 = 11112, 30 = 111102, 60 = 1111002, 120 = 11110002
1024 512 256 128 64 32 16 8 4 2 1 210 29 28 27 26 25 24 23 22 21 20
X10,X8 X2 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111
X10 X16 X2 0 0 0000 1 1 0001 2 2 0010 3 3 0011 4 4 0100 5 5 0101 6 6 0110 7 7 0111 8 8 1000 9 9 1001 10 A 1010 11 B 1011 12 C 1100 13 D 1101 14 E 1110 15 F 1111
- нужно перевести a-1 в двоичную систему счисления;
- сделать инверсию битов: заменить все нули на единицы и единицы на нули в пределах разрядной сетки
Решение 1 задания ЕГЭ
1_1: Разбор 1 задания ЕГЭ по информатике 2017 года ФИПИ вариант 1 (Крылов С.С., Чуркина Т.Е.):Сколько единиц в двоичной записи шестнадцатеричного числа 2AC116?
Подобные задания для тренировки
✍ Решение:
- В шестнадцатеричной с-ме счисления числа от 10 до 15 представлены буквами латинского алфавита: A-10, B-11, C-12, D-13, E-14,
- Необходимо вспомнить двоичные коды чисел от 1 до 15 (см. теорию выше на странице), так как для перевода 16-ричного в двоичную с-му достаточно каждую цифру отдельно записать в виде четверки двоичных цифр (тетрады):
2 A C 1 0010 1010 1100 0001
Результат: 6
Подробный разбор 1 задания с объяснением просмотрите на видео:
1_2: 1 задание. Демоверсия ЕГЭ 2018 информатика (ФИПИ):
Сколько существует целых чисел x, для которых выполняется неравенство 2A16<x<618?
В ответе укажите только количество чисел.
Подобные задания для тренировки
✍ Решение:
- Переведем 2A16 в десятичную систему счисления:
2A16 = 2*161+10*160 = 32 + 10 = 42
618 = 6*81+1*80 = 48 + 1 = 49
42
<), то количество целых, удовлетворяющих условию:49 - 42 - 1 = 6
Результат: 6
Подробное решение данного 1 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
1_3: 1 задание. ГВЭ 11 класс по информатике 2018 (ФИПИ):
Сколько значащих цифр в двоичной записи десятичного числа 129?
1) 6
2) 2
3)
4) 8
✍ Решение:
- Выполним перевод из десятичной с-мы счисления в двоичную делением на 2, справа будем записывать остатки:
129 / 1 64 / 0 32 / 0 16 / 0 8 / 0 4 / 0 2 / 0 1
10000001
Результат: 4
1_4: Решение 1 задания ЕГЭ по информатике (контрольный вариант экзаменационной работы 2018 года, С.С. Крылов, Д.М. Ушаков):
Сколько существует натуральных чисел x, для которых выполняется неравенство
1010112 8?
В ответе укажите только количество чисел.
✍ Решение:
Подробный разбор решения тренировочного варианта предлагаем посмотреть на видео:
1_5: Разбор 1 задания ЕГЭ вариант № 1, 2019 Информатика и ИКТ Типовые экзаменационные варианты (10 вариантов), С.С. Крылов, Т.Е. Чуркина::
Вычислите значение выражения AE16 – 1916.
В ответе запишите вычисленное значение в десятичной системе счисления.
Подобные задания для тренировки
✍ Решение:
- Переведем уменьшаемое и вычитаемое в десятичную систему счисления:
1 0 A E = 10*161 + 14*160 = 160 + 14 = 174* A16 соответствует числу 10 в десятичной системе счисления
* E16 соответствует числу 14 в десятичной системе счисления
1 0 19 = 1*161 + 9*160 = 16 + 9 = 25
174 - 25 = 149
Результат: 149
1_6: Разбор 1 задания ЕГЭ (с сайта К. Полякова, вариант 104 со ссылкой на Носкина А.Н.):
Петя и Коля загадывают натуральные числа. Петя загадал число Х, а Коля число У. После того, как Петя прибавил к Колиному числу 9, а Коля к Петиному числу 20, сумма полученных чисел при записи в двоичной системе счисления представляет собой пять единиц.
Чему равна изначальная сумма загаданных мальчиками чисел? Ответ запишите в двоичной системе счисления. Основание указывать не надо.
✍ Решение:
- Перепишем условие задачи в более понятном виде:
(x + 9) + (y + 20) = 111112 (x + y)2 = ?
111112 = 3110 31 - 20 - 9 = 2
210 = 102
Результат: 10
1_7: Разбор 1 задания ЕГЭ (с сайта К. Полякова, вариант 105 со ссылкой на Куцырь Е.В.):
Укажите наибольшее четырёхзначное восьмеричное число, четверичная запись которого содержит ровно 2 тройки, не стоящие рядом. В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно.
✍ Решение:
- Вспомним, что в восьмеричной системе максимальная цифра 7, а в четверичной — 3. Попробуем выполнить перевод наибольшего восьмеричного числа в четверичную систему, не учитывая условие с нестоящими подряд тройками. Выполним перевод через двоичную систему счисления:
77778 - максимальное четырехзначное восьмеричное число Перевод в двоичную с.с: 7 7 7 7 111 111 111 111 Перевод из двоичной с.с. в четверичную осуществляется делением на группы по две цифры: 11 11 11 11 11 11 3 3 3 3 3 3
11 10 11 10 10 10 3 2 3 2 2 24
111 011 101 010 7 3 5 2
Результат: 7352
1_8: Разбор 1 задания ЕГЭ (с сайта К. Полякова, вариант 109 со ссылкой на Носкина А.Н.):
Задан отрезок [a, b]. Число a – наименьшее число, восьмеричная запись которого содержит ровно 3 символа, один из которых – 3. Число b – наименьшее число, шестнадцатеричная запись которого содержит ровно 3 символа, один из которых – F.
Определите количество натуральных чисел на этом отрезке (включая его концы).
✍ Решение:
- Перепишем условие задачи в более понятном виде, подставив значения для чисел a и b:
a: 1038 - наименьшее трехразрядное восьмеричное число, одна из цифр которого – 3 b: 10F16- наименьшее трехразрядное 16-е число, одна из цифр которого – F
1038 = 6710 10F16 = 27110 [a,b] = [67,271] длина отрезка = 271 - 67 + 1 (включая его концы) = 205
Результат: 205
1_9: Решение 1 задания ЕГЭ 2020 (Тематические тренировочные задания, 2020 г., Самылкина Н.Н., Синицкая И.В., Соболева В.В.):Для хранения целого числа со знаком используется один байт.
Сколько единиц содержит внутреннее представление числа (-116)?
✍ Решение:
- Для перевода отрицательного числа в двоичную систему счисления воспользуемся следующим алгоритмом:
- Из модуля исходного числа вычтем единицу:
|-116| - 1 = 115
11510 = 11100112
01110011
10001100
Результат: 10001100
Сегодня разберём теоретический аспект 1 задания из ЕГЭ по информатике. В данном задании нужно уметь переводить числа из различных систем счисления в другие. Основными системами счисления являются: двоичная, восьмеричная, десятичная (наша родная) и шестнадцатиричная.
Перевод чисел из двоичной системы в шестнадцатиричную систему счисления.
Для начала нужно написать себе в черновик следующую таблицу:

Давайте рассмотрим данную таблицу. В первом столбце идут числа от 0 до 15 в нашей родной десятичной системе счисления. Во втором столбце идут числа так же от 0 до 15, но уже в двоичной системе, а в третьем тоже от 0 до 15 в шестнадцатиричной системе счисления.
Написать числа от 0 до 15 в нашей родной десятичной системе не у кого затруднений не вызовет.
Числа в двоичной же системе лучше всего написать по следующему правилу: в младшем разряде чередуем ноль и единицу, в следующем разряде чередование нулей и единиц происходит в два раза медленнее (два нуля, две единицы, два нуля и т.д.), в следующем разряде ещё в два раза медленнее чередование (4 нуля, 4 единицы и т.д.) и наконец 8 нулей и 8 единиц — в самом старшем разряде.
В шестнадцатиричной системе счисления помимо наших привычных символов от 0 до 9 придуманы символы A, B, С, D, E, F, и из этих 16 символов (от 0 до 15) составляется любое число, так же как в нашей системе составляется любое число из десяти цифр (от 0 до 9).Соответственно, чтобы посчитать от 0 до 15 — нужно перебрать все символы, которые имеются в шестнадцатиричной системе (от 0 до F).
Теперь рассмотрим, как с помощью данной таблицы переводить из двоичной системы в шестнадцатиричную. Переведём число 100101000 из двоичной системы в шестнадцатиричную.
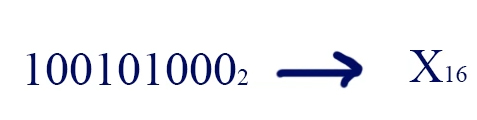
Чтобы выполнить данную задачу, необходимо разбить наше двоичное число по 4 цифры начиная с правого края, и каждую 4-ку цифр нужно найти в нашей таблице: 1000 — это будет 8, 0010 — 2, 0001 -это 1. В старшем разряде у нас осталась одна единица, мы её дополнили 3-мя нулями.

Значит число 1001010002 в двоичной системе счисления будет 12816 в шестнадцатиричной.
Перевод чисел из двоичной системы в восьмеричную
систему счисления.
Из двоичной системы в восьмеричную систему X2 -> X8 переводим точно так же, только теперь из таблицы берём не по четыре цифры, а по три цифры.
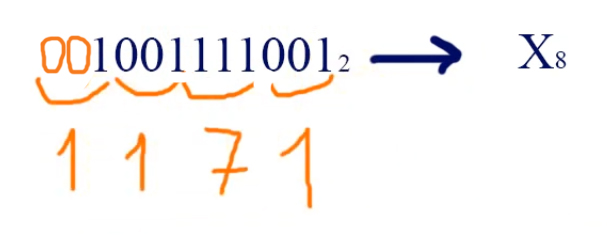
Таким образом, число 10011110012 в двоичной системе будет равно 11718 в восьмеричной системе.
Перевод чисел из шестнадцатиричной системы в двоичную
систему счисления.
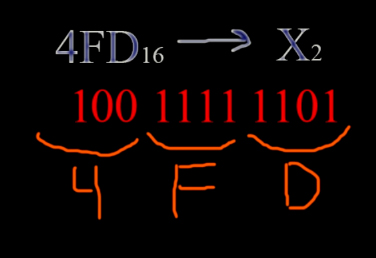
Делаем точно так же, как и при переводе чисел из двоичной в шестнадцатиричную, но в обратном порядке. По таблице смотрим: D — 1101, F — 1111, 4 — 0100. Получается число 010011111101. Слева нули мы отбрасываем 10011111101.
4FD16 -> 100111111012.
Перевод чисел из восьмеричной системы в двоичную
систему счисления.
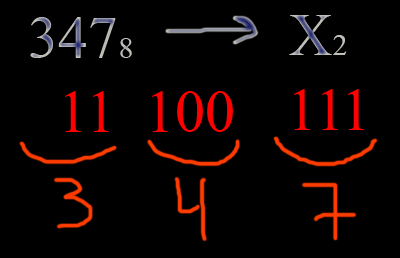
Поступаем, как мы поступали ранее. Разбиваем каждую цифру восьмеричной системы по 3 цифры двоичной системы, используя таблицу, которая приведена в начале статьи. Нули слева откидываем.
3478 -> 111001112.
Перевод чисел из двоичной системы в десятичную
систему счисления.
Переведём число:
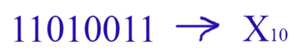
Берём цифры двоичного числа, начиная с младшего разряда (т.е. справа), и начинаем умножать на двойку в соответствующей степени. Степень начинается с нуля и с каждым разом увеличивается на 1. Все эти произведения суммируем.

После вычисления получаем число в десятичной системе:

Результат 110100112 -> 21110
Перевод чисел из десятичной системы в двоичную
систему счисления.
Рассмотрим, как перевести из десятичной системы в двоичную. Возьмём число 213.
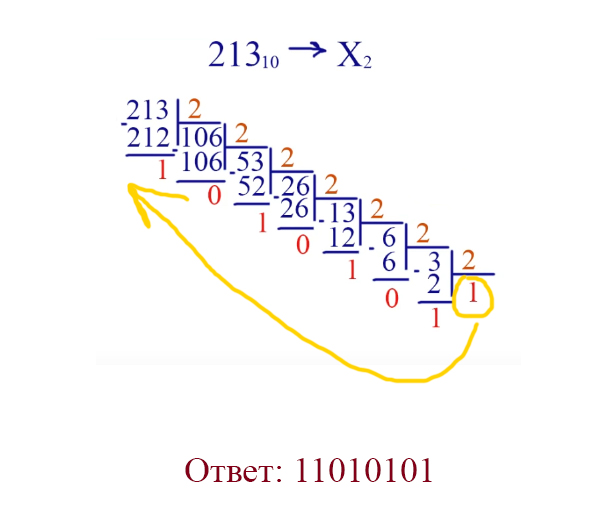
Перевод чисел из шестнадцатиричной системы в восьмеричную систему
счисления и обратно.
Переведём число A10 из шестнадцатиричной системы в восьмеричную A1016 -> X8.
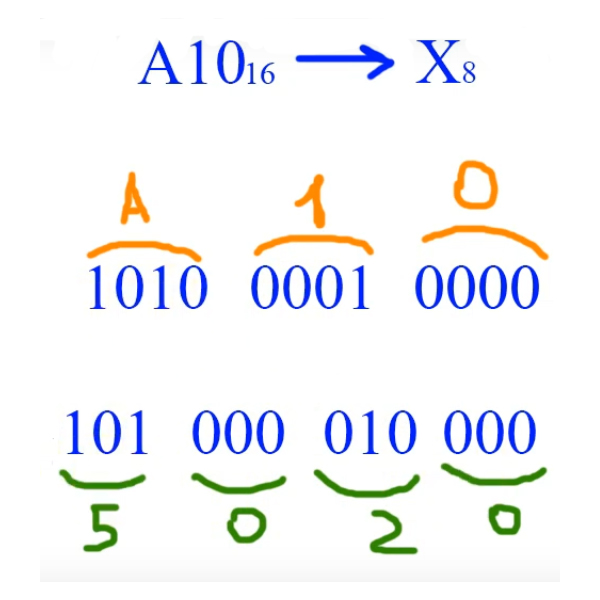
Разбиваем каждую цифру шестнадцатиричного кода по 4-ри цифры двоичного кода из таблицы в начале статьи (Т.е. переводим число в двоичную систему). Полученное число разбиваем по три цифры — и собираем число уже в восьмеричной системе — как показано на рисунке. Обратно переводим аналогично, только в обратном порядке.
Перевод чисел из шестнадцатиричной системы в десятичную
систему счисления.
Переведём число 5B3 из шестнадцатиричной системы в десятичную систему счисления 5B316 -> X10.
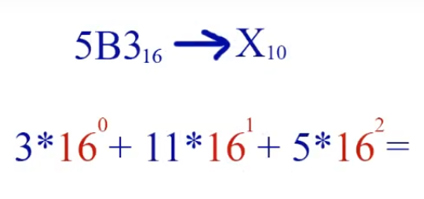
Действуем точно также, как при переводе из двоичной системы в десятичную, только умножаем цифры на 16 в соответствующей степени. Буквы превращаем в десятичные числа из таблицы. Начинаем, как всегда, справа, т.е. с младшего разряда.

Перевод чисел из десятичной системы в шестнадцатиричную
систему счисления.
Переведём число 203 из десятичной системы в шестнадцатиричную систему счисления 20310 -> X16
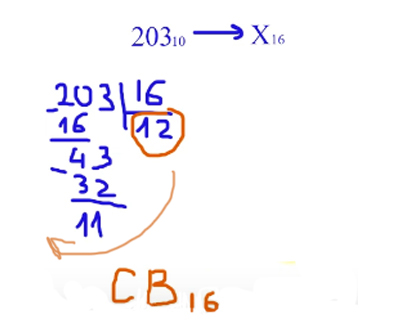
Делим число на 16 до тех пор пока не получится число от 1 до 15. Записываем остатки в обратном порядке. Числа от 10 до 15 превращаем в буквы.
Перевод чисел из восьмеричной системы в десятичную
систему счисления.
Переведём число 347 из восьмеричной системы в десятичную систему счисления 3478 -> X10

Делаем аналогично предыдущим примерам, только теперь умножаем на 8 в соответствующей степени.
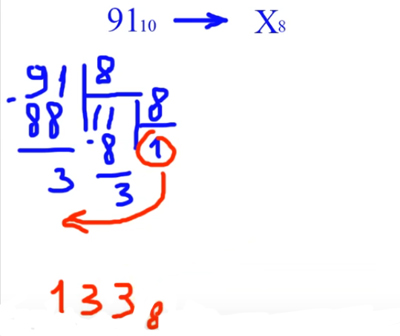
Перевод чисел из десятичной системы в восьмиричную
систему счисления.
Делаем аналогично предыдущим примерам.
 Счастливых экзаменов!
Счастливых экзаменов!Задание 1 ЕГЭ по информатике 2020
За правильное выполненное задание получишь 1 балл. На решение отводится примерно 1 минута.
Для выполнения задания 1 по информатике необходимо знать:
В двоичной системе:
- четные числа оканчиваются на 0, нечетные – на 1;
- числа, которые делятся на 4, оканчиваются на 00, и т.д.; числа, которые делятся на 2k, оканчиваются на k нулей
- числа вида 2k записываются в двоичной системе как единица и k нулей, например: 16 = 24 = 100002
- числа вида 2k-1записываются в двоичной системе k единиц, например: 15 = 24-1 = 11112
- Степени числа 2 : 20=1, 21=2, 22=4, 23=8, 24=16, 25=32, 26=64, 27=128, 28=256, 29=512, 210=1024
Ниже преставленна таблица для перевода чисел из двоичной в восьмеричную, шестнадцатиричную системы и обратно.
| 10 | 2 | 8 | 16 |
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 8 | |
| 9 | 1001 | 9 | |
| 10 | 1010 | A | |
| 11 | 1011 | B | |
| 12 | 1100 | C | |
| 13 | 1101 | D | |
| 14 | 1110 | Е | |
| 15 | 1111 | F |
Задача №16. Разбор различных типов задач.
Автор — Лада Борисовна Есакова.
Перед тем, как приступить к решению задач, нам нужно понять несколько несложных моментов.
Рассмотрим десятичное число 875. Последняя цифра числа (5) – это остаток от деления числа 875 на 10. Последние две цифры образуют число 75 – это остаток от деления числа 875 на 100. Аналогичные утверждения справедливы для любой системы счисления:
Последняя цифра числа – это остаток от деления этого числа на основание системы счисления.
Последние две цифры числа – это остаток от деления числа на основание системы счисления в квадрате.
Например, . Разделим 23 на основание системы 3, получим 7 и 2 в остатке (2 – это последняя цифра числа в троичной системе). Разделим 23 на 9 (основание в квадрате), получим 18 и 5 в остатке (5 = ).
Вернемся опять к привычной десятичной системе. Число = 100000. Т.е. 10 в степени k– это единица и k нулей.
Аналогичное утверждение справедливо для любой системы счисления:
Основание системы счисления в степени k в этой системе счисления записывается как единица и k нулей.
Например, .
1. Поиск основания системы счисления
Пример 1.
В системе счисления с некоторым основанием десятичное число 27 записывается в виде 30. Укажите это основание.
Решение:
Обозначим искомое основание x. Тогда .Т.е. x = 9.
Ответ: 9
Пример 2.
В системе счисления с некоторым основанием десятичное число 13 записывается в виде 111. Укажите это основание.
Решение:
Обозначим искомое основание x. Тогда
Решаем квадратное уравнение, получаем корни 3 и -4. Поскольку основание системы счисления не может быть отрицательным, ответ 3.
Ответ: 3
Пример 3
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
Решение:
Если в некоторой системе число 29 оканчивается на 5, то уменьшенное на 5 число (29-5=24) оканчивается на 0. Ранее мы уже говорили, что число оканчивается на 0 в том случае, когда оно без остатка делится на основание системы. Т.е. нам нужно найти все такие числа, которые являются делителями числа 24. Эти числа: 2, 3, 4, 6, 8, 12, 24. Заметим, что в системах счисления с основанием 2, 3, 4 нет числа 5 (а в формулировке задачи число 29 оканчивается на 5), значит остаются системы с основаниями: 6, 8, 12,
Ответ: 6, 8, 12, 24
Пример 4
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.
Решение:
Если в некоторой системе число оканчивается на 13, то основание этой системы не меньше 4 (иначе там нет цифры 3).
Уменьшенное на 3 число (71-3=68) оканчивается на 10. Т.е. 68 нацело делится на искомое основание системы, а частное от этого при делении на основание системы дает в остатке 0.
Выпишем все целые делители числа 68: 2, 4, 17, 34, 68.
2 не подходит, т.к. основание не меньше 4. Остальные делители проверим:
68:4 = 17; 17:4 = 4 (ост 1) – подходит
68:17 = 4; 4:17 = 0 (ост 4) – не подходит
68:34 = 2; 2:17 = 0 (ост 2) – не подходит
68:68 = 1; 1:68 = 0 (ост 1) – подходит
Ответ: 4, 68
2. Поиск чисел по условиям
Пример 5
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?
Решение:
Для начала выясним, как выглядит число 25 в системе счисления с основанием 4.
. Т.е. нам нужно найти все числа, не больше , запись которых оканчивается на 11. По правилу последовательного счета в системе с основанием 4,
получаем числа и . Переводим их в десятичную систему счисления:
Ответ: 5, 21
3. Решение уравнений
Пример 6
Решите уравнение:
Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).
Решение:
Переведем все числа в десятичную систему счисления:
Квадратное уравнение имеет корни -8 и 6. (т.к. основание системы не может быть отрицательным). .
Ответ: 20
4. Подсчет количества единиц (нулей) в двоичной записи значения выражения
Для решения этого типа задач нам нужно вспомнить, как происходит сложение и вычитание «в столбик»:
При сложении происходит поразрядное суммирование записанных друг под другом цифр, начиная с младших разрядов. В случае, если полученная сумма двух цифр больше или равна основанию системы счисления, под суммируемыми цифрами записывается остаток от деления этой суммы на основание системы, а целая часть от деления этой суммы на основание системы прибавляется к сумме следующих разрядов.
При вычитании происходит поразрядное вычитание записанных друг под другом цифр, начиная с младших разрядов. В случае, если первая цифра меньше второй, мы «занимаем» у соседнего (большего) разряда единицу. Занимаемая единица в текущем разряде равна основанию системы счисления. В десятичной системе это 10, в двоичной 2, в троичной 3 и т.д.
Пример 7
Сколько единиц содержится в двоичной записи значения выражения: ?
Решение:
Представим все числа выражения, как степени двойки:
В двоичной записи двойка в степени n выглядит, как 1 и n нулей. Тогда суммируя и , получим число, содержащее 2 единицы:

Теперь вычтем из получившегося числа 10000. По правилам вычитания занимаем у следующего разряда.

Теперь прибавляем к получившемуся числу 1:

Видим, что у результата 2013+1+1=2015 единиц.
Ответ: 2015.
Вариант 1
система счисления – ДВОИЧНАЯ
1) Переведите число 12 из десятичной в ДВОИЧНУЮ
2) Переведите число 196 из десятичной в ДВОИЧНУЮ
3) Переведите число 1011 из ДВОИЧНОЙ в десятичную
4) Переведите число 101111100 из ДВОИЧНОЙ в десятичную
5) Выполните арифметические действия:
a) 11100000+1010011110
б) 1001001011-111111110
в) 101000*1000011
г) 100000101010/10110
система счисления – ВОСЬМЕРИЧНАЯ
1) Переведите число 47 из десятичной в ВОСЬМЕРИЧНУЮ
2) Переведите число 502 из десятичной в ВОСЬМЕРИЧНУЮ
3) Переведите число 65 из ВОСЬМЕРИЧНОЙ в десятичную
4) Переведите число 1412 из ВОСЬМЕРИЧНОЙ в десятичную
система счисления – ШЕСТНАДЦАТЕРИЧНАЯ
1) Переведите число 91 из десятичной в ШЕСТНАДЦАТЕРИЧНУЮ
2) Переведите число 481 из десятичной в ШЕСТНАДЦАТЕРИЧНУЮ
3) Переведите число 5C из ШЕСТНАДЦАТЕРИЧНОЙ в десятичную
4) Переведите число 35C из ШЕСТНАДЦАТЕРИЧНОЙ в десятичную
Вариант 2
система счисления – ДВОИЧНАЯ
1) Переведите число 28 из десятичной в ДВОИЧНУЮ
2) Переведите число 626 из десятичной в ДВОИЧНУЮ
3) Переведите число 1001111 из ДВОИЧНОЙ в десятичную
4) Переведите число 10111011 из ДВОИЧНОЙ в десятичную
5) Выполните арифметические действия:
a) 110110101+1010001111
б) 1110110010-1110011100
в) 100101*11000
г) 10000000010/110110
система счисления – ВОСЬМЕРИЧНАЯ
1) Переведите число 21 из десятичной в ВОСЬМЕРИЧНУЮ
2) Переведите число 662 из десятичной в ВОСЬМЕРИЧНУЮ
3) Переведите число 77 из ВОСЬМЕРИЧНОЙ в десятичную
4) Переведите число 732 из ВОСЬМЕРИЧНОЙ в десятичную
система счисления – ШЕСТНАДЦАТЕРИЧНАЯ
1) Переведите число 61 из десятичной в ШЕСТНАДЦАТЕРИЧНУЮ
2) Переведите число 586 из десятичной в ШЕСТНАДЦАТЕРИЧНУЮ
3) Переведите число 2C из ШЕСТНАДЦАТЕРИЧНОЙ в десятичную
4) Переведите число 1EF из ШЕСТНАДЦАТЕРИЧНОЙ в десятичную
Вариант 3
система счисления – ДВОИЧНАЯ
1) Переведите число 81 из десятичной в ДВОИЧНУЮ
2) Переведите число 653 из десятичной в ДВОИЧНУЮ
3) Переведите число 1001010 из ДВОИЧНОЙ в десятичную
4) Переведите число 1001000101 из ДВОИЧНОЙ в десятичную
5) Выполните арифметические действия:
a) 1110011101+1100001101
б) 1101100010-11111001
в) 11010*1010001
г) 111101100000/1010010
система счисления – ВОСЬМЕРИЧНАЯ
1) Переведите число 44 из десятичной в ВОСЬМЕРИЧНУЮ
2) Переведите число 804 из десятичной в ВОСЬМЕРИЧНУЮ
3) Переведите число 17 из ВОСЬМЕРИЧНОЙ в десятичную
4) Переведите число 1432 из ВОСЬМЕРИЧНОЙ в десятичную
система счисления – ШЕСТНАДЦАТЕРИЧНАЯ
1) Переведите число 91 из десятичной в ШЕСТНАДЦАТЕРИЧНУЮ
2) Переведите число 946 из десятичной в ШЕСТНАДЦАТЕРИЧНУЮ
3) Переведите число 21 из ШЕСТНАДЦАТЕРИЧНОЙ в десятичную
4) Переведите число 34F из ШЕСТНАДЦАТЕРИЧНОЙ в десятичную
Вариант 4
система счисления – ДВОИЧНАЯ
1) Переведите число 38 из десятичной в ДВОИЧНУЮ
2) Переведите число 241 из десятичной в ДВОИЧНУЮ
3) Переведите число 101001 из ДВОИЧНОЙ в десятичную
4) Переведите число 101000011 из ДВОИЧНОЙ в десятичную
5) Выполните арифметические действия:
a) 11110100+1011101100
б) 1101100110-100100101
в) 111011*1101
г) 1000011000100/111010
система счисления – ВОСЬМЕРИЧНАЯ
1) Переведите число 73 из десятичной в ВОСЬМЕРИЧНУЮ
2) Переведите число 343 из десятичной в ВОСЬМЕРИЧНУЮ
3) Переведите число 15 из ВОСЬМЕРИЧНОЙ в десятичную
4) Переведите число 562 из ВОСЬМЕРИЧНОЙ в десятичную
система счисления – ШЕСТНАДЦАТЕРИЧНАЯ
1) Переведите число 37 из десятичной в ШЕСТНАДЦАТЕРИЧНУЮ
2) Переведите число 105 из десятичной в ШЕСТНАДЦАТЕРИЧНУЮ
3) Переведите число 5C из ШЕСТНАДЦАТЕРИЧНОЙ в десятичную
4) Переведите число 264 из ШЕСТНАДЦАТЕРИЧНОЙ в десятичную
Задачи на Системы счисления
4
Задачи на системы счисления
Найти сумму чисел 378 и 648 в восьмеричной системе счисления.
Найти сумму чисел 3A16 и 648 в восьмеричной системе счисления.
Найти сумму чисел 378 и B416 в восьмеричной системе счисления.
Найти разность чисел 6358 и 4768 в восьмеричной системе счисления.
Чему равна сумма чисел 438 и 5616?
Количество значащих нулей в двоичной записи десятичного числа 126 равно:
1) 1 2) 2 3) 3 4) 0
Перевести число 15FC16 в десятичную систему счисления.
Перевести число 1011012 в десятичную систему счисления.
Перевести число 101,112 в десятичную систему счисления.
Перевести десятичную дробь 0,1875 в двоичную и восьмеричную системы счисления.
Перевести двоичное число 1101111010111011112 в шестнадцатеричную систему счисления.
Дано а = D716, b = 3318. Какое из чисел c, записанных в двоичной системе, отвечает условию a < c < b?
1) 110110012 2) 110111002 3) 110101112 4) 110110002
Количество цифр в двоичной записи десятичного числа, которое можно представить в виде 2 + 8 + 16 + 64 + 128 + 256 + 512, равно:
1) 7 2) 8 3) 9 4) 10
Укажите через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101. Ответ запишите в десятичной системе счисления.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
Укажите наименьшее основание системы счисления, в которой запись числа 19 трехзначна.
В системе счисления с некоторым основанием число 12 записывается в виде 110. Укажите это основание.
В таблице ниже представлена часть кодовой таблицы ASCII:
Символ | 1 | 5 | A | B | Q | a | b |
Десятичный код | 49 | 53 | 65 | 66 | 81 | 97 | 98 |
Шестнадцатеричный код | 31 | 35 | 41 | 42 | 51 | 61 | 62 |
Каков шестнадцатеричный код символа «q» ?
1) 7116 2) 8316 3) А116 4) В316
Сколько единиц в двоичной записи числа 195?
1) 5 2) 2 3) 3 4) 4
Количество значащих нулей в двоичной записи десятичного числа 128 равно:
1) 6 2) 7 3) 8 4) 0
Как представлено число 8310 в двоичной системе счисления?
1) 10010112 2) 11001012 3) 10100112 4) 1010012
Как представлено число 2510 в двоичной системе счисления?
1) 10012 2) 110012 3) 100112 4) 110102
Сколько единиц в двоичной записи десятичного числа 194,5?
1) 5 2) 6 3) 3 4) 4
Вычислите сумму двух двоичных чисел x и y, если x = 10101012 и y = 10100112.
1) 100101102 2) 110010102 3) 101001102 4) 101010002
Вычислите значение суммы 102 + 108 + 1016 в двоичной системе счисления.
1) 10100010 2) 11110 3) 11010 4) 10100
Вычислите сумму чисел X и Y, если X = 1101112, Y = 1358. Результат представьте в двоичном виде.
1) 11010100 2) 10100100 3)10010011 4) 10010100
Значение выражения 1016 + 108·102 в двоичной системе счисления равно:
1) 10102 2) 110102 3) 1000002 4) 1100002
Дано а = 5716, b = 1678. Какое из чисел c, записанных в двоичной системе, отвечает условию a < c < b?
1) 10001102 2) 10001112 3) 11001112 4) 11101112
Дано а = 2128, b = 14316. Какое из чисел c, записанных в двоичной системе, отвечает условию a < c < b?
1) 110000110 2) 100100011 3) 101100011 4) 1110111
Дано А = 9D16, B = 2378. Какое из чисел C, записанных в двоичной системе, отвечает условию A < C < B?
1) 10011010 2) 10011110 3) 10011111 4) 11011110
В таблице ниже представлена часть кодовой таблицы ASCII:
Символ | 1 | 5 | A | B | P | a | b |
Десятичный код | 49 | 53 | 65 | 66 | 80 | 97 | 98 |
Шестнадцатеричный код | 31 | 35 | 41 | 42 | 50 | 61 | 62 |
Каков шестнадцатеричный код символа «p»?
1) 71 2) 70 3) А1 4) В3
В таблице ниже представлена часть кодовой таблицы ASCII:
Символ | 1 | 5 | A | B | a | b | r |
Десятичный код | 49 | 53 | 65 | 66 | 97 | 98 | 114 |
Шестнадцатеричный код | 31 | 35 | 41 | 42 | 61 | 62 | 72 |
Каков шестнадцатеричный код символа «R»?
1) A0 2) 72 3) А2 4) 52
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием 4 оканчивается на 11.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
В системе счисления с некоторым основанием десятичное число 49 записывается в виде 100. Укажите это основание.
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 80, запись которых в системе счисления с основанием 5 оканчивается на 10.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
В системе счисления с некоторым основанием десятичное число 129 записывается в виде 1004. Укажите это основание.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 40 оканчивается на 4.
Укажите, сколько раз используется цифра 3 при записи чисел 13, 14, 15, …, 22, 23 в системе счисления с основанием 4.
Укажите, сколько раз используется цифра 2 при записи чисел 13, 14, 15, …, 22, 23 в системе счисления с основанием 3.
В непозиционной системе счисления, которая называется системой остатков (СО), в качестве оснований выбираются взаимно простые числа, например, p1=3, p2=5, p3=7. При этом диапазон однозначного представления чисел равен произведению оснований (в приведенном примере p1∙p2∙p3 = 105, т. е. однозначно представляются все числа от 0 до 104). Любое число в этом диапазоне записывается остатками от целочисленного деления этого числа на выбранные основания. Например, число A = 19 запишется в СО с основаниями 3, 5, 7 так: A = (1, 4, 5). Укажите, какая из записей соответствует числу 5, записанному в системе остатков с основаниями 3, 5, 7.
1) (3, 0, 2) 2) (2, 0, 2) 3) (2, 0, 5) 4) (5, 5, 5)
В непозиционной системе счисления, которая называется системой остатков (СО), в качестве оснований выбираются взаимно простые числа, например, p1=3, p2=5, p3=7. При этом диапазон однозначного представления чисел равен произведению оснований (в приведенном примере p1∙p2∙p3 = 105, т. е. однозначно представляются все числа от 0 до 104). Любое число в этом диапазоне записывается остатками от целочисленного деления этого числа на выбранные основания. Например, число A = 19 запишется в СО с основаниями 3, 5, 7 так: A = (1, 4, 5). Укажите, какая из записей соответствует числу 3, записанному в системе остатков с основаниями 3, 5, 7.
1) (3, 0, 0) 2) (0, 3, 3) 3) (0, 2, 4) 4) (3, 3, 3)
В саду 100 фруктовых деревьев — 14 яблонь и 42 груши. Найдите основание системы счисления, в которой указаны числа.
Найдите основание системы счисления, в которой выполнено следующее сложение: 144 + 24 = 201.
Найдите основание системы счисления, в которой выполнено следующее умножение: 3213 = 1043.
Дано А=9516, B=2278. Какое из чисел C, записанных в двоичной системе, отвечает условию A<C<B?
1) 10011010 2) 10010111 3) 10010110 4) 11010110
Вычислите сумму чисел x и y при x = 1D16, y = 728.
Результат представьте в двоичной системе счисления.
1) 100011112 2) 11001012 3) 1010112 4) 10101112
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 32, запись которых в системе счисления с основанием три оканчивается на 10.
Запишите число 5678 в двоичной системе счисления.
1) 1011111012 2) 1001101112 3) 1011101112 4) 10001101112
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 100, запись которых в системе счисления с основанием 5 оканчивается на 11.
Дано а = 2528, b = AC16. Какое из чисел c, записанных в двоичной системе, отвечает условию a < c < b?
1) 10101011 2) 10101010 3) 10101111 4) 10101100
Вычислите сумму чисел x и y, при x = A616, y = 758.
Результат представьте в двоичной системе счисления.
1) 110110112 2) 111100012 3) 111000112 4) 100100112
В системе счисления с некоторым основанием число 17 записывается в виде 101. Укажите это основание.
Сколько единиц содержится в двоичной записи десятичного числа 173?
1) 7 2) 5 3) 6 4) 4
Вычислите сумму чисел x и y, при x = A116, y = 11012. Результат представьте в десятичной системе счисления.
1) 204 2) 152 3) 183 4) 174
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 39 оканчивается на 3.
Даны два числа: a = DD16, b = 3378. Какое из чисел c, записанных в двоичной системе, удовлетворяет неравенству a < c < b?
1) 11011110 2) 10111010 3) 11101101 4) 11101111
Чему равна сумма чисел x и y, если x = 2D16, y = 578.
1) 100001002 2) 10111002 3) 2728 4) 8416
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в системе счисления с основанием 5 оканчивается на 3.
двоичной системы счисления
Двоичный номер состоит только из 0 с и 1 с.
110100 |
| Пример двоичного числа |
В Binary нет 2, 3, 4, 5, 6, 7, 8 или 9!
« бит » — это один b начальный символ это . Число выше имеет 6 бит.
Двоичные числа имеют много применений в математике и за ее пределами.
На самом деле цифровой мир использует двоичные цифры.
Как мы считаем, используя бинарные?
Это все равно что считать в десятичном виде, за исключением того, что мы достигаем 10 намного раньше.
| Binary | ||
| 0 | Мы начинаем с 0 | |
| 1 | Тогда 1 | |
| ??? | Но тогда нет символа для 2… что мы делаем? |
| Ну, как мы считаем в десятичном формате? | |||
| 0 | Начало в 0 | ||
| … | Количество 1,2,3,4,5,6,7,8, а затем … | ||
| 9 | Это последняя цифра в десятичной системе | ||
| 10 | Итак, мы снова начинаем с 0, но добавляем 1 слева | ||
То же самое делается в двоичном формате…
| Binary | |||
| 0 | Начало в 0 | ||
| • | 1 | Тогда 1 | |
| •• | 10 | Теперь снова начните с 0, но добавьте 1 слева | |
| ••• | 11 | еще 1 | |
| •••• | ??? | Но СЕЙЧАС что…? |
| Что происходит в десятичном формате? | |||
| 99 | Когда у нас заканчиваются цифры, мы … | ||
| 100 | … снова начните с 0, но добавьте 1 слева | ||
И это то, что мы делаем в двоичном формате…
| Binary | |||
| 0 | Начало в 0 | ||
| • | 1 | Тогда 1 | |
| •• | 10 | Начните снова с 0, но добавьте 1 слева | |
| ••• | 11 | ||
| •••• | 100 | снова начните с 0 и добавьте единицу к числу слева… … но это число уже равно 1, поэтому оно также возвращается к 0 … … и 1 добавляется к следующей позиции слева | |
| ••••• | 101 | ||
| •••••• | 110 | ||
| ••••••• | 111 | ||
| •••••••• | 1000 | Начните снова с 0 (для всех 3 цифр), добавьте 1 слева | |
| ••••••••• | 1001 | и так далее! |
Посмотрите, как это делается в этой маленькой демонстрации (нажмите кнопку воспроизведения):
Десятичный и двоичный
Вот некоторые эквивалентные значения:
| Десятичное число: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Binary: | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Симметрия
Двоичные числа также имеют красивый и элегантный рисунок:
Вот некоторые большие значения:
| Десятичное число: | 20 | 25 | 30 | 40 | 50 | 100 | 200 | 500 |
|---|---|---|---|---|---|---|---|---|
| Binary: | 10100 | 11001 | 11110 | 101000 | 110010 | 1100100 | 11001000 | 111110100 |
«Двоичный файл так же просто, как 1, 10, 11.»
Теперь посмотрим, как использовать двоичный код для подсчета пальцев за тысячу раз:
Позиция
В десятичной системе есть единицы, десятки, сотни и т. Д.
В Binary есть Единицы, Двойки, Четверки и т. Д., Как это:
Это 1 × 8 + 1 × 4 + 0 × 2 + 1 + 1 × (1/2) + 0 × (1/4) + 1 × (1/8)
= 13,625 в десятичном виде
Номера могут быть размещены слева или справа от точки, чтобы показать значения больше одного и меньше одного.
| 10,1 | |
| Число слева от точки целое число (например, 10) | |
| По мере продвижения влево, каждое число с номером получает 2 раз больше . | |
| Первая цифра справа означает половин (1/2). | |
| По мере продвижения вправо, каждое число становится в раза в 2 раза меньше, чем (вдвое больше). | |
Пример: 10,1
- «10» означает 2 в десятичном виде,
- «.1» означает половину,
- Итак, «10,1» в двоичном виде — это 2,5 в десятичном виде.
Вы можете выполнять преобразования из двоичного в десятичное в шестнадцатеричное преобразование.
слов
Слово двоичное происходит от «Би-«, что означает два. Мы видим «би» в таких словах, как «велосипед» (два колеса) или «бинокль» (два глаза).
| Когда вы произносите двоичное число, произносите каждую цифру (например, двоичное число «101» произносится как «один ноль один» или иногда «один-о-один» ). Таким образом, люди не путаются с десятичным числом. |
Одна двоичная цифра (например, «0» или «1») называется «бит».
Например, 11010 имеет длину пять битов.
Слово , бит состоит из слов « b начальная цифра it »
Как показать, что число является двоичным
Чтобы показать, что число является двоичным числом , добавьте к нему маленькое число 2, например: 101 2
Таким образом, люди не будут думать, что это десятичное число «101» (сто один).
Примеры
Пример: Что такое 1111 2 в десятичном формате?
- «1» слева находится в положении «2 × 2 × 2», что означает 1 × 2 × 2 × 2 (= 8)
- Следующий «1» находится в положении «2 × 2», что означает 1 × 2 × 2 (= 4)
- Следующий «1» находится в положении «2», что означает 1 × 2 (= 2)
- Последний «1» находится в позиции единиц, что означает 1
- Ответ: 1111 = 8 + 4 + 2 + 1 = 15 в десятичной дроби
Пример: что такое 1001 2 в десятичном формате?
- «1» слева находится в положении «2 × 2 × 2», что означает 1 × 2 × 2 × 2 (= 8)
- «0» находится в положении «2 × 2», что означает 0 × 2 × 2 (= 0)
- Следующий «0» находится в позиции «2», что означает 0 × 2 (= 0)
- Последний «1» находится в позиции единиц, что означает 1
- Ответ: 1001 = 8 + 0 + 0 + 1 = 9 в десятичной дроби
Пример: что такое 1.1 2 в десятичном формате?
- «1» на левой стороне — в позиции единиц, что означает 1.
- 1 с правой стороны находится в положении «половинки», что означает 1 × (1/2)
- Итак, 1.1 — это «1 и 1 половина» = 1,5 в десятичном виде
Пример: Что такое 10.11 2 в десятичном формате?
- «1» находится в положении «2», что означает 1 × 2 (= 2)
- «0» находится в положении единиц, так что означает 0
- «1» справа от точки находится в положении «половинки», что означает 1 × (1/2)
- Последняя «1» с правой стороны находится в положении «четверти», что означает 1 × (1/4)
- Итак, 10.11 — это 2 + 0 + 1/2 + 1/4 = 2,75 в десятичном виде
«В мире есть 10 видов людей,
из которых понимают двоичные числа, а те, кто не понимает».
Двоичная система счисления
Основное различие между двоичной системой счисления и нашей знакомой базовой системой счисления 10 состоит в том, что группирование выполняется в группы по 2 вместо 10.
Например, чтобы представить 24 в базе 10 с помощью палочек, вы можете использовать две группы по десять и 4, как показано ниже.
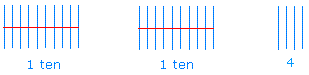
Следует помнить о чем-то важном, и это ключ к пониманию этого урока!
- Цифры 0,1,2,3,4,5,6,7,8,9 используются для представления всех возможных чисел.Обратите внимание, что база 10 имеет 10 цифр
- Зависит от того, насколько велико это число, мы делаем группы из десяти, сотен, тысяч, десяти тысяч и т. Д. (Это мощность 10: 10 1 = 10, 10 2 = 100, 10 3 = 1000)
- Если число меньше 10, например, 8 и 9, создавать группы не нужно. И это число займет однозначное значение
- Если число больше 9 и меньше 100, например, 10, 55 и 98, необходимо создать группы из десяти.Группы из десяти будут занимать десятые места.
- Если число больше 99 и меньше 1000, например, 100, 255 и 999, необходимо создать группы из сотен. Группы сотен будут занимать сотни мест.
- и так далее …
 |
Так как число больше 99, мы должны были сделать группы по сто десять.Обратите также внимание на то, как группы из сотен помещаются в десятые места, а группы из десяти — в десятки.
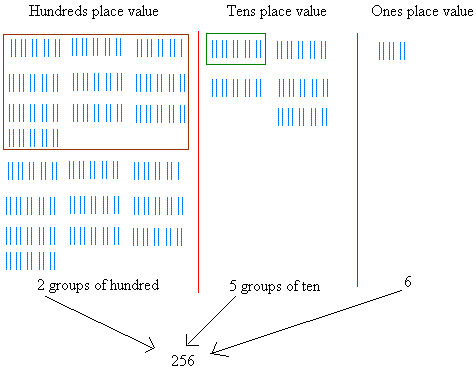 |
Аналогичным образом, двоичная система счисления имеет свое собственное значение.
- Цифры 0,1 используются для представления всех возможных чисел в двоичной системе счисления. Обратите внимание, что база 2 имеет 2 цифры для представления всех возможных чисел.
- В зависимости от того, насколько велико число, мы делаем группы по 2, 4, 8, 16, 32 и т. Д… (Это мощность 2: 2 1 = 2, 2 2 = 4, 2 3 = 8)
- Если число меньше 2 для примера 1, создавать группы не нужно. И этот номер займёт первое место, значение . Это значение соответствует местам в базе 10
- На самом деле это 1 одинаково в двоичной системе и в системе 10.
- Если число больше 1 и меньше 4, например, 2 и 3, необходимо создать группу из двух.Группа из двух человек займет , второе место — значение . Вы также можете назвать это «два» место стоимость
- Если число больше 3 и меньше 8, например 4 и 7, необходимо создать группу из четырех человек. Группа из четырех человек займет , третье место — значение . Вы также можете назвать это «четыре» место стоимость
- Если число больше 7 и меньше 16, например, 8, 11 и 14, необходимо создать группу из восьми. Группа из восьми займет , четвертое место — значение .Вы также можете назвать это «восьмеркой».
- Если число больше 15 и меньше 32, например, 16, 21 и 30, необходимо создать группу из шестнадцати. Группа из шестнадцати будет занимать пятое место, значение . Вы также можете назвать это «шестнадцатеричной» ценностью.
- Если число больше 31 и меньше 64, например, 32, 45 и 63, необходимо создать группу из тридцати двух. Группа из тридцати двух человек займёт , шестое место стоит .Вы также можете назвать это «тридцать два» места стоимости.
- и так далее …
Ну, это означает, что мы можем создать только 1 группу, а не 2, а не 3
, так как мы используем только 0 и 1 для представления чисел , будет невозможно записать двоичные числа, используя число 2.
Теперь давайте преобразуем 25 в двоичную систему счисления
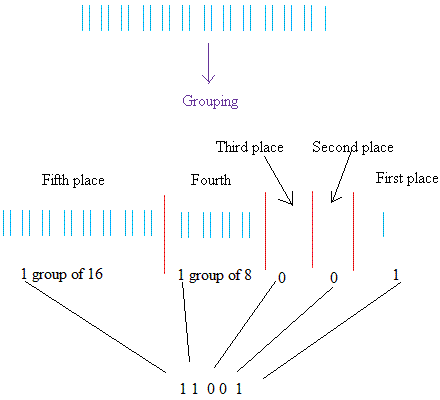 |
Обратите внимание, что нет группировок по два и четыре.В результате на втором месте ставятся нули, а на третьем месте
Как производится группировка в двоичной системе счисления. Как конвертировать из базы 10 в базу 2
Группа с n-го места на первое. Это означает, что вы должны сначала создать группу с максимально возможной мощностью 2
. Например, я пытаюсь преобразовать 45 в двоичную систему счисления.
Задай себе вопрос. Какая максимальная мощность 2 меньше 45?
2 6 = 64. 2 5 = 32.Таким образом, наибольшая сила 2 меньше 45 равна 2 5 = 32
Поскольку 32 идет на шестом месте, поставьте 1 на , на шестом месте . Затем попытайтесь выяснить, что входит в стоимость места раньше.
45-32 = 13
Задайте себе вопрос. Какая максимальная мощность 2 меньше 13?
2 4 = 16. 2 3 = 8. Таким образом, максимальная мощность 2 меньше 13 равна 2 3 = 8
Поскольку 8 идет на четвертом месте, поставьте 1 на на четвертом месте Затем попытайтесь выяснить, что входит в стоимость места раньше.
13-8 = 5
Задайте себе вопрос. Какая максимальная мощность 2 меньше 5?
2 3 = 8. 2 2 = 4. Таким образом, наибольшая мощность 2 меньше 5 равна 2 2 = 4
Поскольку 4 идет на третьем месте, поставьте 1 на на третьем месте Затем попытайтесь выяснить, что входит в стоимость места раньше.
5-4 = 1 и 1 выходит на первое место .
Обратите внимание, что вы ничего не ставите на пятое и второе места, поэтому в этих местах идут нули
Следовательно, 45, преобразованное в двоичную систему счисления, это 101101
Вы также можете написать 45 десять или 101101 два
Будьте очень осторожны, когда читаете 101101 два ! 101101 2 считывается один ноль один один ноль одна база 2
Новые уроки математики
Ваша электронная почта в безопасности с нами.Мы будем использовать его только для информирования вас о новых уроках математики.
,Системы счисления!
Теория чисел и как работают двоичные числа.
Введение
Числа вокруг нас, и по большей части мы принимаем их как должное. Если бы я предложил вам 1337 долларов, вы были бы счастливы, потому что знаете, что это довольно разумное количество долларов. Система счисления является средством представления количества вещей.Десятичная дробь — это всего лишь одна из нескольких систем счисления, хотя другие, в двоичном виде, важны для понимания в различных областях, особенно в вычислительных.
В нашем введении для начинающих в двоичные, шестнадцатеричные и восьмеричные числа вы изучите двоичные преобразования и арифметику с интерактивными демонстрациями и подробными объяснениями.
Наброски
Этот двоичный учебник состоит из 3 разделов. В общем, я рекомендую вам проработать их по порядку, но если вы пришли сюда просто, чтобы узнать какую-то конкретную тему, то кто я такой, чтобы замедлять вас, просто идите прямо.
- Системы счисления
- — читайте ниже, чтобы узнать теорию чисел.
- Преобразования — Как преобразовать двоичное и десятичное, шестнадцатеричное и восьмеричное.
- Арифметика — Узнайте, как выполнять различные арифметические операции с двоичными числами.
- Отрицательные числа — Узнайте, как управлять отрицательными числами в двоичном виде.
- С плавающей запятой и дроби — Узнайте, как преобразовать десятичные числа в двоичные дроби и с плавающей запятой.
Шаблоны и ярлыки
Когда вы работаете с системами счисления, вы можете воспользоваться несколькими краткими инструкциями:
- облегчают работу с ними.
- поможет проверить вашу работу / выявить глупые ошибки, которые вы, возможно, допустили.
Я укажу некоторые из них, когда мы прорабатываем материал, но вы всегда должны следить за ними самостоятельно (не только в работе с числами, но и в других областях).
В общем, вы хотите следить за паттернами, а затем подумать о том, как вы можете использовать эти паттерны для своей выгоды. С практикой вы становитесь лучше, замечая их.
Десятичная система
Десятичная система счисления — это та, с которой мы больше всего знакомы, мы используем ее каждый день. Десятичная дробь — это то, что мы называем позиционной системой счисления. То есть положение цифр дает значение значению, которое они представляют. Другие системы счисления (двоичная, шестнадцатеричная и восьмеричная) также позиционные, поэтому, как только мы поймем основную теорию десятичных чисел, мы сможем легко применить ее для понимания других систем.
Давайте рассмотрим пример:
Если у меня есть номер 31415, то, что это на самом деле представляет собой:
30000 + 1000 + 400 + 10 + 5
Или точнее:
| 3 * 10 4 | 30000 |
| 1 * 10 3 | 1000 |
| 4 * 10 2 | 400 |
| 1 * 10 1 | 10 |
| 5 * 10 0 | 5 |
Десятичное число составляет основание 10 .Это означает, что у нас есть 10 символов для представления значений (0 — 9). По мере продвижения по каждой позиции мы умножаем это число на 10 до степени этой позиции (начиная с 0 в крайней правой части).
Помните: все в степени 0 всегда 1
Десятичная дробь удобна как система счисления, так как каждый раз, когда мы увеличиваем мощность, все, что нам нужно сделать, это добавить еще 0. Для каждой цифры в числе, добавить число 0, необходимое для позиции, и вы получите ее позиционное значение.Тогда каждая цифра естественно выстраивается в общем числе.
Binary
Binary следует тому же шаблону, что и Decimal, за исключением того, что вместо того, чтобы быть основанием 10, он вместо является основанием 2 . Вместо 10 символов для представления значений у нас есть два (0 и 1).
Итак, десятичная система — это базовая система счисления 10, мы имеем 10 символов и умножаем на степени 10. Из этого следует, что двоичная система является системой счисления 2, мы имеем два символа и умножаем на степени 2.
Давайте рассмотрим пример:
Если у меня есть двоичное число 101010, оно переводится в десятичное число как:
32 + 0 + 8 + 0 + 2 + 0 = 42
или:
| 1 * 2 5 | 32 |
| 0 * 2 4 | 0 |
| 1 * 2 3 | 8 |
| 0 * 2 2 | 0 |
| 1 * 2 1 | 2 |
| 0 * 2 0 | 0 |
Как видно из этого примера, двоичный файл не так удобен, как десятичный, для чтения и работы с людьми.Так что вы можете спросить: зачем тогда работать с двоичным кодом? Ответ в том, что это более простой формат для работы с компьютерами. Он также может быть использован в других областях в качестве ярлыка для представления настроек.
Поскольку все степени 2, кроме 0, приводят к четному числу, единственный способ получить нечетное число состоит в том, чтобы самая правая цифра равнялась 1. Это можно использовать для быстрой проверки при выполнении преобразований, которые вы не сделали глупая ошибка.
шестнадцатеричный и октальный
Две другие системы счисления, которые обычно используются в вычислениях — это шестнадцатеричная и восьмеричная.Это также базовые системы счисления.
- Шестнадцатеричное основание 16
- Восьмеричное основание 8
Оба они тесно связаны с двоичным. Вы заметите, что:
Это не относится к десятичной системе счисления (нет степени 2, равной 10). Это дает шестнадцатеричные и восьмеричные характеристики по отношению к двоичным, которые не имеют десятичные. Мы рассмотрим их в следующем разделе, конверсии.
Для шестнадцатеричного мы идем до 15 (помните, мы начинаем с 0). Как только мы доберемся до 9, мы добавим буквы алфавита A — F, чтобы обозначить 10 — 15 (см. Справочную таблицу ниже).
Давайте возьмем десятичное число 27.
В шестнадцатеричном виде это будет 1B, что в десятичном виде переводится в:
1 * 16 1 + 11 * 16 0 = 16 + 11
И в восьмеричном это будет 33, что в десятичном виде переводится в:
3 * 8 1 + 3 * 8 0 = 24 + 3
Префиксы
Как видно из приведенных выше примеров, числа могут выглядеть одинаково, независимо от того, являются ли они двоичными, десятичными, восьмеричными или шестнадцатеричными.Если бы я дал вам число 2F7, вы бы сразу поняли, что это шестнадцатеричное число, но если бы я дал вам число 101, то это:
- 101 в двоичном и 5 в десятичном
- 101 в десятичном виде
- 101 в шестнадцатеричном и 257 в десятичном
- 101 в восьмеричной и 65 в десятичной
??
Как видите, количество, которое представляет 101, варьируется в значительной степени в зависимости от базы, которую мы используем.Чтобы избежать этой двусмысленности, мы добавляем префиксы к номерам, чтобы определить их базу.
- Десятичное число не имеет префикса.
- Шестнадцатеричный имеет префикс Ox, например: Ox1B
- Octal имеет префикс O, например: O421
- Binary имеет префикс Ob, например: Ob1101
Некоторые люди вместо этого используют суффиксы, но они не так популярны:
- Десятичное число не имеет суффикса.
- Шестнадцатеричный имеет суффикс H, например: 1BH
- Octal имеет суффикс O, например: 421O
- Binary имеет суффикс B, например: 1101B
Примечание: для префиксов и суффиксов выше это заглавная буква, а не ноль.
Для большей части этого урока я не буду использовать префиксы, но буду определять базу напрямую, чтобы сделать ее более понятной.
Справочная таблица
Вот справочная таблица для различных систем счисления.
| Десятичное число | Binary | Octal | шестнадцатеричный |
|---|---|---|---|
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | С |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Вы заметите, что есть двоичный шаблон.Крайний правый столбец чередуется от 0 до одного. Следующий столбец делает то же самое, но 2 одновременно. Третий столбец делает то же самое, но 4 за раз. Крайний левый столбец делает то же самое, но 8 одновременно. Этот шаблон позволяет легко убедиться, что он написан правильно.
Если вы проводите экзамен по бинарному образцу, вам часто не разрешают брать материал, но ничто не мешает вам самостоятельно составить эту таблицу после начала экзамена. Это может быть хорошим справочником, особенно для конверсий, которые мы рассмотрим в следующем разделе.
Советы
Этот материал может быть немного сложным, чтобы разобраться. Если вы обнаружите, что читая материал, немного подумаете, вот что я предлагаю:
- Работа с примерами на бумаге. Изучать бинарный код — все равно что кататься на велосипеде. Лучший способ — просто сделать это.
- Оставь это через день или два, потом возвращайся и отправляйся еще раз.
Понимание двоичных чисел для начинающих
В моем опыте преподавания сетей многие студенты борются с IP-адресами, потому что им не хватает базового понимания двоичных чисел.
Понимание двоичных чисел, двоичной системы и того, как преобразовывать двоичные числа в десятичные, важно для всех, кто связан с компьютерами, кодированием и сетями.
Binary 101 — Что вы выучите
- Основы числовых баз — База 10, База 2 и База 16
- Как преобразовать двоичные числа в десятичные и наоборот
- Как преобразовать двоичные числа в шестнадцатеричные и наоборот,
- Как преобразовать шестнадцатеричное в десятичное и наоборот,
Обзор системы Base 10 или десятичных чисел
Прежде чем мы узнаем о двоичной системе счисления, мы более подробно рассмотрим нашу обычную десятичную систему счисления.
Принципы одинаковы для всех систем нумерации, и их легче изучить с помощью системы, с которой вы более знакомы.
Во-первых, наша десятичная система использует 10 в качестве базы , а числа варьируются от 0 до 9
Давайте рассмотрим несколько примеров номеров
Мы начинаем с трехзначного числа 129 (сто двадцать девять).
Это составило 100 +20 +9 = 129
Если мы посмотрим на диаграмму ниже, то увидим, что при движении справа налево столбцы увеличиваются в 10 раз.
2 во втором столбце — это не 2, а 2 * 10 = 20, а 1 в третьем столбце — не 1, а 1 * 10 * 10 = 100.
означает 10, возведенное в степень 0. Это равно 1 и представляет столбец наших единиц.
В приведенной ниже краткой таблице показано еще несколько записей с использованием обозначения мощности.
При написании десятичных чисел мы редко пишем значения столбцов над числами, поскольку мы уже знаем, что это такое, поэтому просто пишем:
129 и не
Я ввел обозначение степени, потому что оно является фундаментальным для понимания двоичных чисел.
Минимальное возможное число из трех цифр составляет 000 , а максимальное — 999. Для чисел, больших 999 , нам нужен четвертый столбец, который будет столбцом 1000 с.
Двоичная система счисления
Двоичные числа являются числами из базы 2 и имеют только два значения — 0 и 1.
Если мы посмотрим на двоичное число, например 101, то мы снова можем назначить значения столбцов, как мы делали с нашим десятичным числом, но на этот раз мы используем 2, а не 10 в качестве основания.
Таким образом, двоичное 101 двоичное имеет 1 в столбце единиц, 0 в столбце 2s и 1 в столбце 4s.
Опять же, если мы проходим путь справа налево, то:
1 — это 1, как в столбце единиц, но следующее 1 — это не 1, а 1 * 4 = 4
Двоичные числа используют базу 2, поэтому столбцы
двоичного в десятичное преобразование
Давайте рассмотрим несколько двоичных чисел и преобразуем их в десятичные
Мы начинаем с трехзначного двоичного числа 101 (см. Изображение выше
Число может быть преобразовано в десятичное число путем умножения следующим образом:
1 * 1 + 0 * 2 + 1 * 4 = 5
Максимальное значение, которое мы можем получить с тремя двоичными цифрами, равно 111 = десятичное число 7, рассчитанное следующим образом:
1 * 1 + 1 * 2 + 1 * 4
Больше примеров:
1011 двоичный = 1 * 1 + 1 * 2 + 0 * 4 + 1 * 8 = 11
1111 двоичный = 1 * 1 + 1 * 2 + 1 * 4 + 1 * 8 = 15
Попробуйте сами
1001 двоичный =?
1100 бинарный =?
Преобразование из десятичного в двоичное
Как преобразовать десятичное число в двоичное число.
Пример, что такое десятичное число 10 двоичное число .
Я делаю это, используя следующий список из 2 кратных.
128,64,32,16,8,4,2,1
Вот удобный график
Примечание: ошибка на диаграмме выше должна быть 2 7 = 128
Процедура состоит в том, чтобы вычесть число с наибольшей степенью двойки из десятичного числа
Наибольшая мощность двух чисел р, которую мы можем вычесть, составляет 8 , что составляет 2 3 .
Так 10-8 = 2
мы теперь делаем то же самое с остатком, поэтому наибольшее число, которое мы можем вычесть, равно 2, что = 2 1
2-2 = 0
, поэтому у нас есть 1 восемь, без четверок, 1 два, без единиц = 1010 = 2 3 + 2 1 .
Пример 2 : десятичное 13 для двоичного кода
1 восемь, 1 четыре, 0 два, 1 единица = 1101.
Пример 3 : десятичное число 7 для двоичного кода
0 восемь, 1 четыре, 1 два, 1 единица = 0111.
Ответы, чтобы попробовать сами вопросы
1001 двоичный = 9
1100 двоичный = 12
байтов, октетов и шестнадцатеричных чисел
В компьютерах кодирование и сетевые 8-битные числа распространены.
8-битное число известно как октет , а также чаще оно называется байт . Смотрите вики для деталей.
Бинарное в десятичное и десятичное в двоичное преобразование 8-битные числа
8-битное двоичное число может представлять максимум десятичного 255 = двоичное 11111111 .
Рассчитано следующим образом:
1 * 128 + 1 * 64 + 1 * 32 + 1 * 16 + 1 * 8 + 1 * 4 + 1 * 2 + 1 + 1 = десятичное 255
Вот еще одно 8-битное двоичное число — 01101011.
Чтобы преобразовать его в десятичное, мы пишем число с номерами столбцов выше, следующим образом:
, если мы преобразуем наши столбцы в десятичные эквиваленты, используя следующую таблицу.
, то двоичное число 01101011 = 1 * 1 + 1 * 2 + 0 * 4 = 1 * 8 + 0 * 16 = 1 * 32 + 1 * 64 + 0 * 128
= 64 + 32 + 8 + 2 + 1 = 107
Обратите внимание, состоит только из 1 и 0.
Чтобы преобразовать это число в десятичное, нам нужно понять, что представляет каждый 1.
Если мы напишем значение столбца на с выше чисел, то будет легко преобразовать двоичное число в десятичное.
Пример десятичного в двоичное преобразование
Последний более крупный пример преобразования десятичного числа 200 в двоичный код
200 = 128 + 64 + 8 = 2 7 + 2 6 + 2 3 = 11001000
Как только вы довольны процессом, вы можете использовать калькулятор в десятичной системе счисления , как в Windows.
Это преобразует двоичные числа в десятичные
и преобразует десятичные числа в двоичные
Понимание шестнадцатеричных чисел
Шестнадцатеричное число (основание 16) требует 4 бита и имеет максимальное значение 15 . Используются символы 0-9, A, B, C, D, E, F .
Они представлены в двоичном виде следующим образом:
0000 = 0
0001 = 1
0010 = 2
0011 = 3
0100 = 4
.,
1010 = A
1011 = B
1100 = C
1101 = D
1110 = E
1111 = F
Байт (8 бит) можно представить как два шестнадцатеричных числа.
так
FF = двоичное 11111111 и десятичное 255
F0 = 11110000 двоичное и десятичное 240
Quick Quiz
Двоичные числа Основы Викторина
Информация
Базовый тест студентов на понимание двоичных чисел.
Вы уже прошли викторину раньше. Следовательно, вы не можете начать это снова.
Вы должны войти или зарегистрироваться, чтобы начать тест.
Вы должны закончить следующий тест, чтобы начать этот тест:
Видео
Я создал видео, которое охватывает вышеперечисленное, если вы предпочитаете видео — Понимание видео двоичных чисел
Ресурсы и статьи по теме:
Пожалуйста, оцените? И используйте Комментарии, чтобы сообщить мне больше
[Всего: 69 Среднее: 4.5/5] ,