Двоичная система счисления для букв: Двоичная система счисления — Википедия – двоичный код в текст — двоичная система счисления

двоичный код в текст — двоичная система счисления

Двоичный переводчик

Двоичный переводчик — это инструмент для перевода двоичного кода в текст для чтения или печати. Вы можете перевести двоичный файл на английский, используя два метода; ASCII и Unicode.

---

Двоичная система счисления

Система двоичного декодера основана на числе 2 (основание). Он состоит только из двух чисел как системы счисления base-2: 0 и 1.

Хотя бинарная система применялась в различных целях в древнем Египте, Китае и Индии, она стала языком электроники и компьютеров современного мира. Это наиболее эффективная система для обнаружения выключенного (0) и включенного (1) состояния электрического сигнала. Это также основа двоичного кода в текст, который используется на компьютерах для составления данных. Даже цифровой текст, который вы сейчас читаете, состоит из двоичных чисел. Но вы можете прочитать этот текст, потому что мы расшифровали двоичный код перевод файл, используя двоичный код слова.

---

Двоичное число легче прочитать, чем выглядит: это позиционная система; поэтому каждая цифра двоичного числа возводится в степень 2, начиная с 20 справа. Каждая двоичная цифра в преобразователе двоичного кода относится к 1 биту.

---

Что такое ASCII?

ASCII — это стандарт кодирования символов для электронной связи, сокращенный от Американского стандартного кода для обмена информацией. В компьютерах, телекоммуникационном оборудовании и других устройствах коды ASCII представляют текст. Хотя поддерживается много дополнительных символов, большинство современных схем кодирования символов основаны на ASCII.

---

ASCII — это традиционное название для системы кодирования; Управление по присвоению номеров в Интернете (IANA) предпочитает обновленное имя США-ASCII, которое поясняет, что эта система была разработана в США и основана на преимущественно используемых типографских символах. ASCII является одним из основных моментов IEEE.

---

Бинарный в ASCII

Первоначально основанный на английском алфавите, ASCII кодирует 128 указанных семибитных целочисленных символов. Можно печатать 95 кодированных символов, включая цифры от 0 до 9, строчные буквы от a до z, прописные буквы от A до Z и символы пунктуации. Кроме того, 33 непечатных контрольных кода, полученных с помощью машин Teletype, были включены в исходную спецификацию ASCII; большинство из них в настоящее время устарели, хотя некоторые все еще широко используются, такие как возврат каретки, перевод строки и коды табуляции.

---

Например, двоичное число 1101001 = шестнадцатеричное 69 (i — девятая буква) = десятичное число 105 будет представлять строчный I в кодировке ASCII.

---

Использование ASCII

Как уже упоминалось выше, используя ASCII, вы можете перевести компьютерный текст в человеческий текст. Проще говоря, это переводчик с бинарного на английский. Все компьютеры получают сообщения в двоичном, 0 и 1 серии. Тем не менее, так же, как английский и испанский могут использова

Переводим числа между двоичной и десятичной системами «на лету», объяснение «на пальцах»

Здравствуйте, Хабровцы.
Пост можно было бы назвать: «Для любителей посчитать на пальцах», но это мы узнаем дальше.

Вступление: А что-же тянуть. Все что будет дальше, пойдет на тему подсчета в двоичной системе на пальцах. Кто еще не знает, постараюсь обьяснить, что это, как и зачем это осваивать.
Начну, пожалуй, с преимуществ:
1. Удобно переводить любое число с десятичной в двоичную системы и наоборот, не используя калькулятор.
2. Развивается моторика пальцев.
3. Развивается визуальное восприятие двоичных чисел.
Минусы:
1. Немного тренировки.
2. Нельзя в публичных местах показывать числа 26,27,352,378 и 891.

Суть:
Многим, наверняка, приходилось переводить между системами. И я думаю многие запомнили, что:
2-10
3-11
4-100
5-101
и т.д.
Логично, что исходя из того что каждая разрядность имеет два состояния, мы можем изобразить это дело на пальцах.

Поставьте перед собой руку (ладонью к себе), согните большой палец. Вот и есть единица. Разогните большой и согните указательный, вот и два. Тоесть разогнутый палец — это 0, а согнутый — 1. Так как начальные нули отбросились, мы имеем отсчет от «самой левой» единицы.
Названия пальцев — те которые загнуты:
средний, большой — 101 — 5
безымянный, средний -1100 — 12
мизинец, средний — 10100 — 20
Чтобы загибать мизинец, понадобиться некоторая практика. Но суть в другом. Представим разрядность каждого пальца руки, как 2^n (на фото)

То есть,

Теперь, представим, что нам нужно перевести число 25 в двоичную. Загибаем Мизинец — 16, Безымянный — 8 и большой — 1. т.к. 16+8+1=25.

Если не поняли, то вот еще пример, число 14, думаем: Мизинец — это много, средний нормально, но можно взять больше, поэтому — загибаем безымянный, это 8. Запомнили, далее средний — +4, єто уже 12 и указательный — +2, итог 14.

Так же поступаем с двоичными. Вот например видим где-то: 1011101. Представляем это на руках с разрядностями (уже две руки).

64+16+8+4+1=93
Имеем: 1011101(2) = 93(10)

Заключение: Таким образом мы можем использовать данный метод от 0 до 1023, используя пальцы и обладая элементарной арифметикой. Но при добавлении, хотя бы, одного разряда, можно будет считать до 2047, и далее до 4095, 8191 и т.д. А это могут быть руки, ноги, веки, либо что-то еще что может иметь два состояния 1 и 0.

десятичная, двоичная, таблица перевода чисел

Система счисления – это способ записи чисел с помощью определенных знаков.

Давайте рассмотрим самые распространенные позиционные системы – в зависимости от местоположения (разряда) в записи числа один и тот же знак имеет различные значения.

Целое число “x” в позиционной системе счисления можно выразить следующим образом:

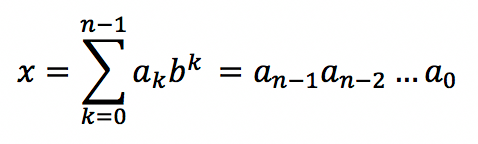
• b – основание системы
• a_k – цифры числа (0 ≤ a_k ≤ b-1)
• k – количество разрядов

Развернутая форма записи целого числа:

Двоичная система счисления: основание – 2

Используется в дискретной математике, информатике и программировании. Содержит только две цифры – 0 и 1. Число, записанное в данной системе, обозначается буквой B на конце (префикс).

Примеры:

• 10101₂ = 10101B = 1×2⁴+0×2³+1×2²+0×2¹+1×2⁰ = 16+4+1= 21
• 10111₂ = 10111B = 1×2⁴+0×2³+1×2²+1×2¹+1×2⁰ = 16+4+2+1= 23
• 100011₂ = 100011B = 1×2⁵+0×2⁴+0×2³+0×2²+1×2¹+1×2⁰ =32+2+1= 35

Восьмеричная система счисления: основание – 8

Для записи числа используются восемь цифр – от 0 до 7.

Примеры:

• 27₈ = 2×8¹+7×8⁰ = 16+7 = 23
• 30₈ = 3×8¹+0×8⁰ = 24
• 4307₈ = 4×8³+3×8²+0×8¹+7×8⁰= 2247

Десятичная система счисления: основание -10

Самая распространенная система, которая используется повсеместно. Содержит цифры от 0 до 9.

Пример:

2538₁₀ = 2×10³+5×10²+3×10¹+8×10⁰

Шестнадцатеричная система счисления: основание – 16

Используются цифры от 0 до 9, а также буквы от A до F. Для обозначения чисел служит префикс H. Система применяется в информатике и программировании.

Примеры:

• 28₁₆ = 28H = 2×16¹+8×16⁰ = 40
• 2F₁₆ = 2FH = 2×16¹+15×16⁰ = 47
• BC12₁₆ = BC12H = 11×16³+12×16²+1×16¹+2×16⁰= 48146

Таблица соответствия чисел систем счисления

Двоичная система	Восьмеричная система	Десятичная система	Шестнадцатеричная система
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10
17	10001	21	11
18	10010	22	12
19	10011	23	13
20	10100	24	14
21	10101	25	15
22	10110	26	16
23	10111	27	17
24	11000	30	18
25	11001	31	19
26	11010	32	1A
27	11011	33	1B
28	11100	34	1C
29	11101	35	1D
30	11110	36	1E
31	11111	37	1F
32	100000	40	20

microexcel.ru

Двоичная система счисления — это… Что такое Двоичная система счисления?

Системы счисления в культуре
Индо-арабская система счисления
Арабская Индийские Тамильская Бирманская	Кхмерская Лаоская Монгольская Тайская
Восточноазиатские системы счисления
Китайская Японская Сучжоу Корейская	Вьетнамская Счётные палочки
Алфавитные системы счисления
Абджадия Армянская Ариабхата Кириллическая	Греческая Эфиопская Еврейская Катапаяди
Другие системы
Вавилонская Египетская Этрусская Римская	Аттическая Кипу Майская
Позиционные системы счисления
Десятичная система счисления (10)
2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60
Нега-позиционная система счисления
Симметричная система счисления
Смешанные системы счисления
Фибоначчиева система счисления
Непозиционные системы счисления
Единичная (унарная) система счисления
Список систем счисления

Двоичная система счисления — позиционная система счисления с основанием 2.

Двоичные цифры

В этой системе счисления числа записываются с помощью двух символов (0 и 1).

История

• В 1605 году Френсис Бэкон описал систему, буквы алфавита которой могут быть сведены к последовательностям двоичных цифр, которые в свою очередь могут быть закодированы как едва заметные изменения шрифта в любых случайных текстах. Важным шагом в становлении общей теории двоичного кодирования является замечание о том, что указанный метод может быть использован применительно к любым объектам.^[7] (См. Шифр Бэкона)

• Современная двоичная система была полностью описана Лейбницем в XVII веке в работе Explication de l’Arithmétique Binaire^[8]. В системе счисления Лейбница были использованы цифры 0 и 1, как и в современной двоичной системе. Как человек, увлекающийся китайской культурой, Лейбниц знал о книге Перемен и заметил, что гексаграммы соответствуют двоичным числам от 0 до 111111. Он восхищался тем, что это отображение является свидетельством крупных китайских достижений в философской математике того времени.^[9]

• В 1937 году Клод Шеннон представил к защите кандидатскую диссертацию Символический анализ релейных и переключательных схем в MIT, в которой булева алгебра и двоичная арифметика были использованы применительно к электронным реле и переключателям. На диссертации Шеннона по существу основана вся современная цифровая техника.

• В ноябре 1937 года Джордж Штибиц, впоследствии работавший в Bell Labs, создал на базе реле компьютер «Model K» (от англ. «Kitchen», кухня, где производилась сборка), который выполнял двоичное сложение. В конце 1938 года Bell Labs развернула исследовательскую программу во главе со Штибицом. Созданный под его руководством компьютер, завершённый 8 января 1940 года, умел выполнять операции с комплексными числами. Во время демонстрации на конференции American Mathematical Society в Дартмутском колледже 11 сентября 1940 года Штибиц продемонстрировал возможность посылки команд удалённому калькулятору комплексных чисел по телефонной линии с использованием телетайпа. Это была первая попытка использования удалённой вычислительной машины посредством телефонной линии. Среди участников конференции, бывших свидетелями демонстрации, были Джон фон Нейман, Джон Мокли и Норберт Винер, впоследствии писавшие об этом в своих мемуарах.

Запись двоичных чисел

Двоичная система счисления является комбинацией двоичной системы кодирования и показательной весовой функции с основанием равным 2. Положительные целые числа (без знака) записываются в виде:

где:

•  — представляемое число, первый индекс — основание системы кодирования (размерность множества цифр a={0,1}), второй индекс — основание весовой показательной функции b (в двоично-десятичном кодировании b=10),
•  — запись числа, строка цифровых знаков,
•  — обозначение основания системы кодирования и основания системы счисления,
•  — количество цифр (знаков) в числе x_2,2,
•  — порядковый номер цифры,
•  — цифры числа x_2,2 из множества a={0,1}, в двоичной системе счисления основание системы кодирования равно 2,
•  — основание показательной весовой функции, основание системы счисления,
•  — весовая показательная функция, создающая весовые коэффициенты.

Количество записываемых кодов (чисел) зависит от основания системы кодирования — c, определяется в комбинаторике и равно числу размещений с повторениями:

где:

Количество записываемых кодов (чисел) от основания показательной функции — b не зависит.
Основание показательной функции — b определяет диапазон представляемых числами x_2,b величин и разреженность представляемых чисел на числовой оси.

Целые числа являются частными суммами степенного ряда:

в котором коэффициенты a_n берутся из множества R=a{0,1}, X=2, n=k, а верхний предел в частных суммах ограничен с до — n-1.

Целые числа со знаком записываются в виде:

где:

•  — знак числа из множества z={+,-}, у положительных целых чисел знак зачастую опускается.

Дробные числа записываются в виде:

где:

•  — число цифр дробной части числа,
•  — весовые коэффициенты из множества ,
• основание системы кодирования равно 2,
•  — основание показательной весовой функции, основание системы счисления.

Следует отметить, что число может быть записано в двоичном коде, а система счисления при этом может быть не двоичной, а с другим основанием. Пример: двоично-десятичное кодирование, в котором десятичные цифры записываются в двоичном виде, а система счисления — десятичная.

Сложение, вычитание и умножение двоичных чисел

Таблица сложения

Пример сложения «столбиком» (14 + 5 = 19):

		1	↖
+		1	1	1	0
			1	0	1
	1	0	0	1	1

Таблица вычитания

—	0	1
0	0	1
1	(заём из старшего разряда) 1	0

Таблица умножения

Пример умножения «столбиком» (14 × 5 = 70):

×				1	1	1	0
					1	0	1
+				1	1	1	0
		1	1	1	0
	1	0	0	0	1	1	0

Преобразование чисел

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

512

256

128

64

32

16

8

4

2

1

Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1, называется двоичной точкой.

Преобразование двоичных чисел в десятичные

Допустим, вам дано двоичное число 110001. Для перевода в десятичное просто запишите его справа налево как сумму по разрядам следующим образом:

.

Можно записать это в виде таблицы следующим образом:

512	256	128	64	32	16	8	4	2	1
				1	1	0	0	0	1
				+32	+16				+1

Точно так же, начиная с двоичной точки, двигайтесь справа налево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа.
Таким образом, двоичное число 110001 равнозначно десятичному 49.

Преобразование методом Горнера

Для того, чтобы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47. Перевод дробных чисел методом Горнера 1) 0,1101₂=0,X₁₀ (рассматриваем цифры в обратном порядке)
1:2=0,5
0,5+0=0,5
0,5:2=0,25
0,25+1=1,25
1,25:2=0,625
0,625+1=1,625
1,625:2=0,8125
Ответ: 0,1101₂= 0,8125₁₀
2) 0,356₈=0,X₁₀ (рассматриваем цифры в обратном порядке)
6:8=0,75
0,75+5=5,75
5,75:8=0,71875
0,71875+3=3,71875
3,71875:8=0,46484375
Ответ: 0,356₈=0,46484375₁₀
3) 0,A6E₁₆=0,X₁₀ (рассматриваем цифры в обратном порядке)
14:16=0,875
0,875+6=6,875
6,875:16=0,4296875
0,4296875+10=10,4296875
10,4296875:16=0,65185546875
Ответ: 0,A6E₁₆=0,65185546875₁₀

Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

19 /2 = 9  с остатком 1
9  /2 = 4  c остатком 1
4  /2 = 2  без остатка 0
2  /2 = 1  без остатка 0
1  /2 = 0  с остатком 1

Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справа налево. То есть нижнее число будет самым левым и.т.д. В результате получаем число 19 в двоичной записи: 10011.

Преобразование дробных двоичных чисел в десятичные

Нужно перевести число 1011010,101 в десятичную систему. Запишем это число следующим образом:

Или по таблице:

64	32	16	8	4	2	1	0.5	0.25	0.125
1	0	1	1	0	1	0.	.1	0	1
+64		+16	+8		+2		+0.5		+0.125

Преобразование дробных десятичных чисел в двоичные

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

• Вначале переводится целая часть десятичной дроби в двоичную систему счисления;
• Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;
• В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;
• Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206₁₀=11001110₂ по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:
0,116 • 2 = 0,232
0,232 • 2 = 0,464
0,464 • 2 = 0,928
0,928 • 2 = 1,856
0,856 • 2 = 1,712
0,712 • 2 = 1,424
0,424 • 2 = 0,848
0,848 • 2 = 1,696
0,696 • 2 = 1,392
0,392 • 2 = 0,784
и т. д.
Получим: 206,116₁₀=11001110,0001110110₂

Применения

В цифровых устройствах

Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:

• Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток (ток больше пороговой величины) — нет тока (ток меньше пороговой величины), индукция магнитного поля больше пороговой величины или нет (индукция магнитного поля меньше пороговой величины) и т. д.
• Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину напряжения, тока или индукции магнитного поля, потребуется ввести два пороговых значения и два компаратора, что не будет способствовать помехоустойчивости и надёжности хранения информации.^{[источник не указан 770 дней]}
• Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.

В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует (очевидно) один двоичный разряд двоичного регистра, то есть двоичный триггер с двумя состояниями (0,1).

В английской системе мер

При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7¹⁵/₁₆″, 3¹¹/₃₂″ и т. д.

Интересные факты

См. также

Примеры чисел-степеней двойки

Степень	Значение
0	1
1	2
2	4
3	8
4	16
5	32
6	64
7	128
8	256
9	512
10	1024
11	2048
12	4096
13	8192
14	16384
15	32768
16	65536
17	131072
18	262144
19	524288
20	1048576
21	2097152
22	4194304
23	8388608
24	16777216
25	33554432
26	67108864
27	134217728
28	268435456
29	536870912
30	1073741824
31	2147483648
32	4294967296
33	8589934592
34	17179869184
35	34359738368
36	68719476736
37	137438953472
38	274877906944
39	549755813888
40	1099511627776
41	2199023255552
42	4398046511104
43	8796093022208
44	17592186044416
45	35184372088832
46	70368744177664
47	140737488355328
48	281474976710656
49	562949953421312
50	1125899906842624
51	2251799813685248

Примечания

1. ↑ Sanchez, Julio & Canton, Maria P. (2007), «Microcontroller programming: the microchip PIC», Boca Raton, Florida: CRC Press, с. 37, ISBN 0-8493-7189-9 
2. ↑ W. S. Anglin and J. Lambek, The Heritage of Thales, Springer, 1995, ISBN 0-387-94544-X
3. ↑ Ordish George, Hyams, Edward. The last of the Incas: the rise and fall of an American empire. — New York: Barnes & Noble, 1996. — С. 80. — ISBN 0-88029-595-3
4. ↑ Experts ‘decipher’ Inca strings. Архивировано из первоисточника 18 августа 2011.
5. ↑ Carlos Radicati di Primeglio, Gary Urton Estudios sobre los quipus. — P. 49.
6. ↑ Dale Buckmaster (1974). «The Incan Quipu and the Jacobsen Hypothesis». Journal of Accounting Research 12 (1): 178-181. Проверено 2009-12-24.
7. ↑ Bacon, Francis, «The Advancement of Learning», vol. 6, London, сс. Chapter 1, <http://home.hiwaay.net/~paul/bacon/advancement/book6ch2.html> 
8. ↑ http://www.leibniz-translations.com/binary.htm Leibniz Translation.com EXPLANATION OF BINARY ARITHMETIC
9. ↑ Aiton, Eric J. (1985), «Leibniz: A Biography», Taylor & Francis, сс. 245–8, ISBN 0-85274-470-6 

Ссылки

Двоичные числа — это… Что такое Двоичные числа?

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).

Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:

• Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток — нет тока, индукция магнитного поля больше пороговой величины или нет и т. д.
• Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину индукции магнитного поля, потребуется ввести два пороговых значения, что не будет способствовать помехоустойчивости и надёжности хранения информации.
• Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
• Возможно применение аппарата алгебры логики для выполнения побитовых операций над числами.

В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).

1 + 0 = 1
1 + 1 = 10
10 + 10 = 100

Таблица умножения двоичных чисел

0 • 0 = 0
0 • 1 = 0
1 • 0 = 0
1 • 1 = 1

Использование двоичной системы при измерении дюймами

При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7¹⁵/₁₆″, 3¹¹/₃₂″ и т. д.

Преобразование чисел

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

512

256

128

64

32

16

8

4

2

1

Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.

Преобразование двоичных чисел в десятичные

Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:

512	256	128	64	32	16	8	4	2	1
				1	1	0	0	1	1
				32	+16			+2	+1

Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо .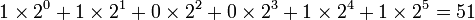

Преобразование методом Горнера

Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.

Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа

Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.

unsigned int to_deg_2(unsigned int num){
  int i;
  if ( num == 1 ) return 2;
  for( num-=1,i=1; i < sizeof(unsigned int)*8; i*=2 ) num = num|(num>>i);
  return num+1;
}

Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

19 /2 = 9  с остатком 1
9  /2 = 4  c остатком 1
4  /2 = 2  с остатком 0
2  /2 = 1  с остатком 0
1  /2 = 0  с остатком 1

Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.

Другие системы счисления

В статье «Системы счисления (продолжение)»^[1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.

См. также

Ссылки

1. ↑ http://potan.livejournal.com/91399.html Системы счисления (продолжение)

Wikimedia Foundation. 2010.