Авитрия что это такое: Авитрия глаза что это такое — Про сосуды – Авитрия глаза это | Видеть Все

Витроэктомия — Википедия

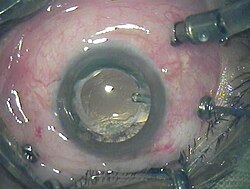Витроэктомия через 3 порта 23 калибра 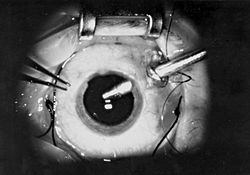Витроэктомия через одиночный порт 19 калибра

Витроэктомия — операция по удалению из глаза части или всего стекловидного тела. Передняя витроэктомия часто преследует цель удаления из передних структур глаза небольших кусочков стекловидного тела, застрявших там. Первичная витроэктомия — общий термин для группы операций, совершаемых в более глубоких частях глаза, которые включают в себя частичное или полное удаление прозрачного желе стекловидного тела.

Витроэктомия был создана Робертом Макемером (Robert Machemer)^[1] при участии Томаса М.Эаберга(Tomas Aaberg Sr) в конце 1969 — начале 1970 года. Первоначальной целью витроэктомии было удаление помутнений стекловидного тела, обычно содержащих кровь.

Успех этих первых процедур привёл к разработке методов и инструментов для удаления помутнения, а также для удаления шрама со светочувствительной подкладки сетчатки глаза — мембраноэктомии, для обеспечения пространства для вводимых в глаз материалов с целью закрепления сетчатки, таких как газы или жидкий силикон, а также для увеличения эффективности других хирургических действий, таких как стяжка склеры.

Разработка новых инструментов и хирургических стратегий в течение 1970-х и 1980-х годов была создана по инициативе хирург/инженера Стива Чарльза (Steve Charles), доктора медицинских наук^[2]. Другие недавние достижения включают в себя более мелкие и более изощрённые внутриглазные инструменты, инъекции различных препаратов в момент операции и при отслоении сетчатки для приведения её в надлежащее положение, пометки слоев ткани, для последующего их удаления, а также для долговременной защиты от образования рубцов.

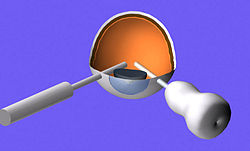Инструменты для витроэктомии

Дополнительные хирургические этапы в рамках современных витроэктомии операций могут включать в себя:

Мембраноэктомию — удаление слоев нездоровой ткани с поверхности сетчатки с помощью крохотных инструментов, таких как пинцеты (крошечный захватывающий инструмент), остроконечных (миниатюрные крючки) и вязко-рассекающих(для отделения слоев ткани в струе жидкости).

Жидко-воздушный обмен — инъекцию воздуха в глаз для удаления внутриглазной жидкости из заднего сегмента глазного яблока, сохраняя при этом внутриглазное давление, чтобы временно удержать сетчатку на месте или для герметизации отверстий в сетчатке. Давление воздуха действует временно, после чего задняя часть будет вновь наполняться жидкостью.

Воздушно-газовый обмен — впрыск газа, или чаще как правило, смеси газа и воздуха, в задний сегмент глазного яблока. В качестве газов обычно используются октафторпропан или гексафторид серы . Газы, которые смешаны с воздухом для нейтрализации их побочных свойств, способны обеспечить более эффективную (чем один воздух) тампонаду сетчатки. Тампонада сетчатки — действие по удержанию сетчатки на её месте или временного закрытия отверстий в сетчатке. Смешанные газы исчезают спонтанно, как только они достигают своей цели, и задний сегмент вновь наполняется жидкостью

[3].

Впрыскивание силиконового масла — заполнение глаза жидким силиконом для фиксации сетчатки^[3].

Фотокоагуляция — лазерная обработка для герметизации отверстия в сетчатке или закрытия нездоровых, поврежденных кровеносных сосудов, которые образуются при некоторых заболеваниях, таких как диабет^[3].

Стяжка склеры — установка поддержки, расположенной подобно поясу вокруг стенок глазного яблока, чтобы поддерживать сетчатку в надлежащем, закрепленном положении.

Линзоэктомия — удаление хрусталика когда он мутный(катаракта), или если он скреплен с тканью шрама^[3].

Витроэктомия показана при:

Деструкция стекловидного тела — плавающие фрагменты различного размера, формы, консистенции, показателя преломления, и подвижности в обычно прозрачном стекловидном теле глаза, которые могут препятствовать зрению. Здесь показана первичная витроэктомия, как было сказано выше, для ослабления симптомов^[4]. Однако из-за возможных побочных эффектов её используют только в тяжелых случаях.

Отслоение сетчатки — ослепляющее состояние, при котором подкладка глаза свободна и свободно плавает в интерьере глаза. Меры для прикрепления сетчатки могут включать витроэктомию, чтобы очистить внутреннее желе, изгиб склеры, чтобы создать опору для возвращения обратно сетчатки, мембраноэктомию для удаления рубцовой ткани, инъекции плотных жидкостей для возвращения сетчатки на место, коагуляция, чтобы прикрепить сетчатку к стенке глаза, и нагнетание газа или силиконового масла, чтобы закрепить сетчатку на месте, пока это заживает.

Макулярная складка — формирование пятачка нездоровой ткани в центральной части сетчатки (макулы) искажающего зрение. Иначе называется эпиретинальная мембрана . После витроэктомии для удаления стекловидного геля, делается мембраноэктомия для удаления ткани.

Диабетическая ретинопатия — может привести к повреждению типа непролиферативной либо пролиферативной ретинопатии. Пролиферативный тип характеризуется образованием новых нездоровых, постоянно кровоточащих сосудов внутри глаза (так называемое витреальное кровоизлияние) и/или в результате чего нарастает толстый волокнистый слой рубцовой ткани на сетчатке — витроэктомия показана для его удаления. Часто диабетическая ретинопатия лечится на ранних стадиях с помощью лазера в кабинете врача, чтобы предотвратить эти проблемы. Когда кровотечение или отслоение сетчатки уже произошло, витроэктомия используется, для удаления крови, мембраноэктомия — рубцовой ткани, а впрыск газа или силикона с застежкой склеры — для возвращения зрения. Больные сахарным диабетом должны ежегодно проверять зрение.

Макулярные повреждения — обычное возрастное уменьшение стекловидного тела иногда может оторвать центральную часть сетчатки, порождая макулярное повреждение со слепым пятном, блокирующим зрение.

Кровоизлияние в стекловидное тело — кровоизлияние в глаз из-за травм, разрывов сетчатки, субарахноидальных кровотечений (как синдром Терсона (Terson)), или тромбов кровеносных сосудов. После удаления крови коагуляция лазером может удалить нездоровые кровеносные сосуды или герметизировать повреждения в сетчатке.

Наряду с обычными осложнениями после операции, такие как инфекции, витроэктомия может привести к отслоению сетчатки. Более частым осложнением является высокое внутриглазное давление, кровотечение в глаз и катаракта, которые являются наиболее частым осложнением хирургической витроэктомии. У многих пациентов развивается катаракта в течение первых нескольких лет после операции

[5].

Пациенты должны использовать глазные капли в течение нескольких недель или больше для заживления поверхности глаза. В некоторых тяжелых случаях следует соблюдать постельный режим в течение нескольких недель. Газовый пузырь может быть размещен внутри глаза, чтобы удерживать сетчатку на месте. Если используется газовый пузырь, то может потребоваться поддержка определенного положения головы, например, лицом вниз или сон только на правой или левой стороне. Очень важно следовать конкретным указаниям врача. Газовый пузырь будет растворяться в течение продолжительного времени, порядка нескольких недель. Следует избегать полетов, пока газовый пузырь не рассосется. Такие проблемы, как возвращение первоначального состояния, кровотечение или послеоперационные инфекции могут потребовать дополнительного лечения или привести к потере зрения. В том случае, если пациенту необходимо лежать лицом вниз после операции, должна быть арендована система поддержки витроэктомии для оказания помощи при реабилитации. Это специальное оборудование может использоваться от пяти дней до трех недель.

Возможность возвращения зрения после витроэктомии зависит от основного заболевания, которое породило необходимость хирургического вмешательства. Если глаз был здоров, но наполнялся кровью, то витрэктомия может привести к возвращению полной остроты зрения 20/20. С более серьёзными проблемами, такими как многократная хирургия сетчатки, остаточное зрение может оказаться достаточным лишь для безопасной ходьбы пешком (амбулаторное зрение) или менее того.

В 1996 году американский актёр, сценарист и драматург Спелдинг Грей (5 июня 1941 — 10 января 2004) выпустил Gray’s Anatomy — фильм-монолог, описывающий его переживания как человека, страдающего от макулярной складки, и своё решение сделать операцию.

1. ↑ MacHemer, R. The development of pars plana vitrectomy: a personal account (англ.) // Graefe’s archive for clinical and experimental ophthalmology = Albrecht von Graefes Archiv fur klinische und experimentelle Ophthalmologie : journal. — 1995. — Vol. 233, no. 8. — P. 453—468. — PMID 8537019.
2. ↑ Wang, CC; Charles, S. Microsurgical instrumentation for vitrectomy: Part II (англ.) // Journal of clinical engineering : journal. — 1984. — Vol. 9, no. 1. — P. 63—71. — DOI:10.1097/00004669-198401000-00015. — PMID 10265855.
3. ↑ ^{1 2 3 4} 16 // Surgical Technology for the Surgical Technologist (англ.). — 2. — Delmar Learning, 2004. — P. 580—581. — ISBN 1-4018-3848-0.
4. ↑ Roth, M; Trittibach, P; Koerner, F; Sarra, G. Pars plana vitrectomy for idiopathic vitreous floaters (англ.) // Klinische Monatsblätter für Augenheilkunde : journal. — 2005. — Vol. 222, no. 9. — P. 728—732. — DOI:10.1055/s-2005-858497. — PMID 16175483.
5. ↑ Benson W. E., Brown G. C., Tasman W., McNamara J. A. Complications of vitrectomy for non-clearing vitreous hemorrhage in diabetic patients (англ.) // Ophthalmic surgery : journal. — 1988. — Vol. 19, no. 12. — P. 862—864. — PMID 3231410.

Авитрия глаза что это такое

Способ хирургического лечения авитрии

Изобретение относится к медицине, а именно к офтальмологии, и может быть использовано для хирургического лечения авитрии, возникающей ятрогенно, при лечении различной виреоретинальной патологии, методом, сопряженным с удалением стекловидного тела.

Известны хирургические способы лечения витреопатологии, основанные на частичном или полном удалении стекловидного тела путем витрэктомии с его последующим восполнением физиологическим раствором. При регматогенной отслойке сетчатки прибегают к временной тампонаде витреальной полости силиконом с целью ретиноретенции до формирования хориоретинальных спаек (Столяренко Г.Е., Сдобникова С.В. Микроинвазивная витреоретинальная хирургия: возможности и перспективы//V Всероссийская научная конференция молодых ученых «Актуальные проблемы офтальмологии»: сб. науч. статей. — М., 2010. — С.21. T. Ueta, Y. Yamaquchi, Y. Shirakawa et al. Robot-assisted vitreoretinal surqery. Development of a prototype and feasibility studies in an animal mobel // Ophthalmoloqy. — 2009. — Vol.116. — P.1538-1543).

Недостатком вышеуказанного способа является лишение глаза стекловидного тела, важнейшей структурно-функциональной единицы витреоретинохориоидального комплекса, участвующего в обмене веществ, что приводит к вторичным необратимым изменениям во внутренних оболочках глаза. Кроме того, отсутствие вязкой, формообразующей субстанции в витреальной полости очень часто является причиной возникновения регматогенной отслойки сетчатки, при этом в зоне хирургического вмешательства в ряде случаев развивается грозное осложнение в виде пролиферативного витреоретинального синдрома, несмотря на применение антинеопластических средств. Попытки разработать методы стимуляции репаративной регенерации стекловидного тела, как следует из источников информации, не увенчались успехом и носят экспериментальный характер (Вит. В.В. // Строение зрительной системы человека. — Одесса, 2003. — С. 228).

Задачей изобретения является создание эффективного способа лечения авитрии, обеспечивающего восстановление стекловидного тела с одновременной ретиноретенцией.

Техническим результатом изобретения является стимуляция репаративной регенерации стекловидного тела.

Указанный результат достигается способом хирургического лечения авитрии, включающим аспирацию из витреальной полости физиологического раствора с синхронным восполнением витреальной полости воздухом, с последующим замещением введенного воздуха раствором биоматериала «Аллоплант для стимуляции регенерации стекловидного тела», который вводят в витреальную полость в объеме 3-5 мл канюлированным зондом, причем раствор предварительно готовят в соотношении 100-250 мг Аллопланта на 3-5 мл физиологического раствора.

Используемый биоматериал Аллоплант для стимуляции регенерации стекловидного тела содержит комплекс специфических для стекловидного тела колагеновых компонентов, неколагеновых белков и протеогликанов и максимально приближен по составу к стекловидному телу, что обеспечивает эффективную стимуляцию регенерации стекловидного тела.

Возможность реализации изобретения

Первый этап исследований свойств разработанного стимулятора регенерации стекловидного тела был экспериментальный.

Эксперименты проведены на 18 взрослых кроликах мужского пола (18 глаз) породы шиншилла весом 3-4 кг, содержащихся в стандартных условиях вивария. Методом случайного отбора животные были разделены на 2 группы: в основной группе состояло 12, а в контрольной 6 кроликов.

В основной группе животным на одном глазу (правый глаз) была выполнена ленсвитрэктомия с заполнением витреальной полости вначале воздухом, а затем замещение воздуха биоматериалом Аллоплантом для стимуляции регенерации стекловидного тела согласно предложенному изобретению. Второй глаз оставался интактным.

В контрольной группе кроликам также на одном глазу (правый глаз) была проведена операция ленсвитрэктомия, где, в отличие от основной группы, витреальная полость была заполнена физиологическим раствором.

Животных выводили из эксперимента путем передозировки барбитуратов через 1, 3, 6, 12 месяцев после операции.

В контрольной группе во все сроки после операции в оперированных глазах развился пролиферативный витреоретинальный (ПВР) синдром с тракционной отслойкой сетчатки.

В основной группе во все сроки после операции в оперированных глазах была выявлена регенерация стекловидного тела.

Регенерат был изучен следующими методами: вязкость и, соответственно, наличие волокон было подтверждено путем макро-микроскопического препарирования стекловидного тела. Кроме того, волокна регенерата дополнительно были визуализированы путем введения дипроспана. Морфологические исследования показали, что источником регенерации стекловидного тела является беспигментный эпителий. Коллаген, который содержится в используемом виде Аллопланта, оседал на беспигментном эпителии и являлся матриксом для репаративной регенерации стекловидного тела. В то время как протеогликаны (с преимущественным содержанием гиалуроновой кислоты), также содержащиеся в составе биоматериала Аллоплант, служили морфологическим субстратом для формирования витреофибрилл. Кроме того, дополнительный синтез гиалуроновой кислоты осуществлялся беспигментными клетками, активированными вследствие механического соприкосновения с фрагментами коллагеновых структур биоматериала Аллоплант.

Сущность изобретения поясняется иллюстрациями, где на фиг. 1 показан процесс замещения физиологического раствора на воздух, на фиг. 2 показана замена воздуха в витреальной полости на биоматериал «Аллоплант для стимуляции регенерации стекловидного тела». На чертежах обозначено: 1 — ирригатор, 2 — канюлированный зонд.

Способ осуществляют следующим образом. Производят сквозной разрез роговицы длиной 2 мм на 10 и 17 часах, отступив на 1 мм от лимба. Разрез на 17 часах предназначен для установки ирригатора 1 или канюлированного зонда 2, на 10 часах — эндоиллюминатора, который обеспечивает освещение витреальной полости. Канюлированным зондом аспирируется физиологический раствор, и синхронно витреальная полость заполняется воздухом через ирригатор 1 при помощи пневмопомпы (фиг. 1). Следующим этапом, используя канюлированный зонд 2, витреальную полость заполняют 3-5 мл раствора биоматериала «Аллоплант для стимуляции регенерации стекловидного тела». При этом воздух из витреальной полости выходит пассивно через ирригатор 1 (фиг. 2). Эн

Способ хирургического лечения авитрии

Изобретение относится к медицине, а именно к офтальмологии, и может быть использовано для хирургического лечения авитрии. Для этого из витреальной полости аспирируют физиологический раствор. Синхронно восполняют витреальную полость воздухом. Затем замещают введенный воздух раствором биоматериала «Аллоплант для стимуляции регенерации стекловидного тела». Данный биоматериал вводят в витреальную полость в объеме 3-5 мл канюлированным зондом. Причем раствор предварительно готовят в соотношении 100-250 мг биоматериала на 3-5 мл физиологического раствора. Способ обеспечивает восстановление стекловидного тела после его удаления, что, в свою очередь, улучшает метаболизм структур заднего отдела глазного яблока, ответственных за восприятие. 2 пр., 2 ил.

 

Изобретение относится к медицине, а именно к офтальмологии, и может быть использовано для хирургического лечения авитрии, возникающей ятрогенно, при лечении различной виреоретинальной патологии, методом, сопряженным с удалением стекловидного тела.

Известны хирургические способы лечения витреопатологии, основанные на частичном или полном удалении стекловидного тела путем витрэктомии с его последующим восполнением физиологическим раствором. При регматогенной отслойке сетчатки прибегают к временной тампонаде витреальной полости силиконом с целью ретиноретенции до формирования хориоретинальных спаек (Столяренко Г.Е., Сдобникова С.В. Микроинвазивная витреоретинальная хирургия: возможности и перспективы//V Всероссийская научная конференция молодых ученых «Актуальные проблемы офтальмологии»: сб. науч. статей. — М., 2010. — С.21. T. Ueta, Y. Yamaquchi, Y. Shirakawa et al. Robot-assisted vitreoretinal surqery. Development of a prototype and feasibility studies in an animal mobel // Ophthalmoloqy. — 2009. — Vol.116. — P.1538-1543).

Недостатком вышеуказанного способа является лишение глаза стекловидного тела, важнейшей структурно-функциональной единицы витреоретинохориоидального комплекса, участвующего в обмене веществ, что приводит к вторичным необратимым изменениям во внутренних оболочках глаза. Кроме того, отсутствие вязкой, формообразующей субстанции в витреальной полости очень часто является причиной возникновения регматогенной отслойки сетчатки, при этом в зоне хирургического вмешательства в ряде случаев развивается грозное осложнение в виде пролиферативного витреоретинального синдрома, несмотря на применение антинеопластических средств. Попытки разработать методы стимуляции репаративной регенерации стекловидного тела, как следует из источников информации, не увенчались успехом и носят экспериментальный характер (Вит. В.В. // Строение зрительной системы человека. — Одесса, 2003. — С. 228).

Задачей изобретения является создание эффективного способа лечения авитрии, обеспечивающего восстановление стекловидного тела с одновременной ретиноретенцией.

Техническим результатом изобретения является стимуляция репаративной регенерации стекловидного тела.

Указанный результат достигается способом хирургического лечения авитрии, включающим аспирацию из витреальной полости физиологического раствора с синхронным восполнением витреальной полости воздухом, с последующим замещением введенного воздуха раствором биоматериала «Аллоплант для стимуляции регенерации стекловидного тела», который вводят в витреальную полость в объеме 3-5 мл канюлированным зондом, причем раствор предварительно готовят в соотношении 100-250 мг Аллопланта на 3-5 мл физиологического раствора.

Используемый биоматериал Аллоплант для стимуляции регенерации стекловидного тела содержит комплекс специфических для стекловидного тела колагеновых компонентов, неколагеновых белков и протеогликанов и максимально приближен по составу к стекловидному телу, что обеспечивает эффективную стимуляцию регенерации стекловидного тела.

Возможность реализации изобретения

Первый этап исследований свойств разработанного стимулятора регенерации стекловидного тела был экспериментальный.

Эксперименты проведены на 18 взрослых кроликах мужского пола (18 глаз) породы шиншилла весом 3-4 кг, содержащихся в стандартных условиях вивария. Методом случайного отбора животные были разделены на 2 группы: в основной группе состояло 12, а в контрольной 6 кроликов.

В основной группе животным на одном глазу (правый глаз) была выполнена ленсвитрэктомия с заполнением витреальной полости вначале воздухом, а затем замещение воздуха биоматериалом Аллоплантом для стимуляции регенерации стекловидного тела согласно предложенному изобретению. Второй глаз оставался интактным.

В контрольной группе кроликам также на одном глазу (правый глаз) была проведена операция ленсвитрэктомия, где, в отличие от основной группы, витреальная полость была заполнена физиологическим раствором.

Животных выводили из эксперимента путем передозировки барбитуратов через 1, 3, 6, 12 месяцев после операции.

В контрольной группе во все сроки после операции в оперированных глазах развился пролиферативный витреоретинальный (ПВР) синдром с тракционной отслойкой сетчатки.

В основной группе во все сроки после операции в оперированных глазах была выявлена регенерация стекловидного тела.

Регенерат был изучен следующими методами: вязкость и, соответственно, наличие волокон было подтверждено путем макро-микроскопического препарирования стекловидного тела. Кроме того, волокна регенерата дополнительно были визуализированы путем введения дипроспана. Морфологические исследования показали, что источником регенерации стекловидного тела является беспигментный эпителий. Коллаген, который содержится в используемом виде Аллопланта, оседал на беспигментном эпителии и являлся матриксом для репаративной регенерации стекловидного тела. В то время как протеогликаны (с преимущественным содержанием гиалуроновой кислоты), также содержащиеся в составе биоматериала Аллоплант, служили морфологическим субстратом для формирования витреофибрилл. Кроме того, дополнительный синтез гиалуроновой кислоты осуществлялся беспигментными клетками, активированными вследствие механического соприкосновения с фрагментами коллагеновых структур биоматериала Аллоплант.

Сущность изобретения поясняется иллюстрациями, где на фиг. 1 показан процесс замещения физиологического раствора на воздух, на фиг. 2 показана замена воздуха в витреальной полости на биоматериал «Аллоплант для стимуляции регенерации стекловидного тела». На чертежах обозначено: 1 — ирригатор, 2 — канюлированный зонд.

Способ осуществляют следующим образом. Производят сквозной разрез роговицы длиной 2 мм на 10 и 17 часах, отступив на 1 мм от лимба. Разрез на 17 часах предназначен для установки ирригатора 1 или канюлированного зонда 2, на 10 часах — эндоиллюминатора, который обеспечивает освещение витреальной полости. Канюлированным зондом аспирируется физиологический раствор, и синхронно витреальная полость заполняется воздухом через ирригатор 1 при помощи пневмопомпы (фиг. 1). Следующим этапом, используя канюлированный зонд 2, витреальную полость заполняют 3-5 мл раствора биоматериала «Аллоплант для стимуляции регенерации стекловидного тела». При этом воздух из витреальной полости выходит пассивно через ирригатор 1 (фиг. 2). Эндоиллюминатор для освещения витреальной полости на фигурах не показан ввиду традиционного его использования. Завершающим этапом на роговичные раны накладывают по одному узловому шву.

Биоматериал Аллоплант для стимуляции регенерации стекловидного тела изготавливают из аллогенного донорского стекловидного тела по известной технологии (патент РФ №2189257, МПК A61L 27/00, опубл. 20.09.2002 г.). Донорский материал подвергают физико-химической обработке анионными и катионными детергентами. При этом происходит дозированное разрушение коллагеновых структур и разблокирование химических связей протеогликанов, структурированных в пучках коллагеновых волокон с последующей частичной элиминацией разблокированных гликозаминогликанов. Модифицированная таким образом структура биоматериала позволяет существенно снизить антигенные свойства, сохраняя при этом физико-механические свойства исходной донорской ткани. Из полученного биоматериала после его радиационной стерилизации готовят раствор: 100-250 мг биоматериала на 3-5 мл физраствора.

С применением предлагаемого способа прооперировано 12 пациентов. Из них у семерых до операции диагностирована пролиферативная витреоретинопатия (ПВР синдром) с помутнением стекловидного тела, у пятерых пациентов — увеит с помутнением стекловидного тела. У всех больных отмечен положительный результат операции в виде репаративной регенерации стекловидного тела без признаков патологической пролиферации (ПВР) синдрома. Также наблюдалось и улучшение метаболизма структур заднего отдела глазного яблока, ответственных за зрительное восприятие, что выражалось повышением остроты зрения и расширением полей зрения.

Клинические примеры

Пример 1. Больная Ф., 42 года, с диагнозом хронический увеит, осложненная катаракта, ПВР синдром левого глаза. Ранее хирургическое лечение на левом глазу не предлагалось, а медикаментозное — было неэффективным. Проведенное обследование показало: острота зрения правого глаза — 0,0, левого глаза — инцерта, не коррегирует. Поля зрения глаз не определяются. Внутриглазное давление по Маклакову: правого глаза — 22 мм рт.ст., левого — 21 мм рт.ст. Произведена операция левого глаза по предлагаемому способу с использованием биоматериала Аллоплант для стимуляции регенерации стекловидного тела. Производился сквозной разрез роговицы длиной 2 мм на 10, 14 и 17 часах, отступив на 1 мм от лимба. Разрез на 17 часах предназначен для установки ирригатора или канюлированного зонда, на 14 часах — витреотома, а на 10 часах — эндоиллюминатора. При помощи витреотома в режиме аспирации производилась ленсэктомия с одновременным восполнением внутриглазной жидкости физиологическим раствором через ирригатор. Далее витреотомом производилась витршвартэктомия, освещение витреальной полости в это время обеспечивал эндоиллюминатор, а восполнение объема витреальной полости осуществлялось ирригатором. После удаления стекловидного тела убирали витреотом и канюлированным зондом аспирировали физиологический раствор, и через ирригатор витреальную полость заполняли воздухом при помощи пневмопомпы. Следующим этапом витреальную полость заполняли 5 мл раствором Аллопланта для стимуляции регенерации стекловидного тела. При этом воздух из витреальной полости выходил пассивно через ирригатор. На роговичную рану накладывались узловые швы.

Послеоперационное течение проходило гладко. Больная осмотрена через 2 мес. Глаз спокоен.

При проведении световой биомикроскопии глазное дно просматривается качественно. Диск зрительного нерва бледно-розовый, границы четкие, артерии и вены нормального калибра, а их соотношение равно 2/3. Макулярный рефлекс отсутствует. Наблюдаются признаки хориоретинальной дистрофии, которые заключаются в разрежении сетчатки и хориоидеи. Признаков ПВР синдрома не обнаружено. Острота зрения левого глаза — 0,01. Поля зрения по 8 меридианам составили 157 градусов. Идентичный результат сохранился через 1 год 6 мес.

Пример 2. Больная В., 8 лет с диагнозом ретинопатия недоношенных V степени обоих глаз, воронкообразная отслойка сетчатки. Острота зрения обоих глаз инцерта, не корригируют. Поля зрения глаз не определяются, внутриглазное давление по Маклакову: 18 мм рт.ст. правого глаза, 20 мм рт.ст. — левого. Произведена операция на левый глаз по описанному выше способу. Послеоперационное течение гладкое. Больная осмотрена через 7 мес. Глаз спокоен.

При проведении световой биомикроскопии глазное дно просматривается качественно. Диск зрительного нерва бледноват, границы четкие, артерии и вены узковаты. Макулярный рефлекс отсутствует. Наблюдаются признаки хориоретинальной дистрофии, которые заключаются в разрежении сетчатки и хориоидеи. Признаков ПВР синдрома не обнаружено. Острота зрения левого глаза — счет пальцев. Поля зрения по 8 меридианам составили 114 градусов. Идентичный результат сохранился через 2 года 3 мес.

Таким образом, предложенный способ хирургического лечения авитрии с применением биоматериала Аллоплант для стимуляции регенерации стекловидного тела позволяет восстановить стекловидное тело после его удаления. Ввиду того, что обменные процессы в глазу напрямую зависят от состояния стекловидного тела, данный способ наряду с анатомическим, позволяет получить положительный функциональный результат.

Способ хирургического лечения авитрии, включающий аспирацию из витреальной полости физиологического раствора с синхронным восполнением витреальной полости воздухом, с последующим замещением введенного воздуха раствором биоматериала «Аллоплант для стимуляции регенерации стекловидного тела», который вводят в витреальную полость в объеме 3-5 мл канюлированным зондом, причем раствор предварительно готовят в соотношении 100-250 мг Аллопланта на 3-5 мл физиологического раствора.

Энтропия? Это просто! / Habr

Этот пост является вольным переводом ответа, который Mark Eichenlaub дал на вопрос What’s an intuitive way to understand entropy?, заданный на сайте Quora

Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание.

Если в двух словах, то

Энтропия — это то, как много информации вам не известно о системе

Например, если вы спросите меня, где я живу, и я отвечу: в России, то моя энтропия для вас будет высока, всё-таки Россия большая страна. Если же я назову вам свой почтовый индекс: 603081, то моя энтропия для вас понизится, поскольку вы получите больше информации.

Почтовый индекс содержит шесть цифр, то есть я дал вам шесть символов информации. Энтропия вашего знания обо мне понизилась приблизительно на 6 символов. (На самом деле, не совсем, потому что некоторые индексы отвечают большему количеству адресов, а некоторые — меньшему, но мы этим пренебрежём).

Или рассмотрим другой пример. Пусть у меня есть десять игральных костей (шестигранных), и выбросив их, я вам сообщаю, что их сумма равна 30. Зная только это, вы не можете сказать, какие конкретно цифры на каждой из костей — вам не хватает информации. Эти конкретные цифры на костях в статистической физике называют микросостояниями, а общую сумму (30 в нашем случае) — макросостоянием. Существует 2 930 455 микросостояний, которые отвечают сумме равной 30. Так что энтропия этого макросостояния равна приблизительно 6,5 символам (половинка появляется из-за того, что при нумерации микросостояний по порядку в седьмом разряде вам доступны не все цифры, а только 0, 1 и 2).

А что если бы я вам сказал, что сумма равна 59? Для этого макросостояния существует всего 10 возможных микросостояний, так что его энтропия равна всего лишь одному символу. Как видите, разные макросостояния имеют разные энтропии.

Пусть теперь я вам скажу, что сумма первых пяти костей 13, а сумма остальных пяти — 17, так что общая сумма снова 30. У вас, однако, в этом случае имеется больше информации, поэтому энтропия системы для вас должна упасть. И, действительно, 13 на пяти костях можно получить 420-ю разными способами, а 17 — 780-ю, то есть полное число микросостояний составит всего лишь 420х780 = 327 600. Энтропия такой системы приблизительно на один символ меньше, чем в первом примере.

Мы измеряем энтропию как количество символов, необходимых для записи числа микросостояний. Математически это количество определяется как логарифм, поэтому обозначив энтропию символом S, а число микросостояний символом Ω, мы можем записать:

S = log Ω

Это есть ничто иное как формула Больцмана (с точностью до множителя k, который зависит от выбранных единиц измерения) для энтропии. Если макросостоянию отвечают одно микросостояние, его энтропия по этой формуле равна нулю. Если у вас есть две системы, то полная энтропия равна сумме энтропий каждой из этих систем, потому что log(AB) = log A + log B.

Из приведённого выше описания становится понятно, почему не следует думать об энтропии как о собственном свойстве системы. У системы есть опеделённые внутренняя энергия, импульс, заряд, но у неё нет определённой энтропии: энтропия десяти костей зависит от того, известна вам только их полная сумма, или также и частные суммы пятёрок костей.

Другими словами, энтропия — это то, как мы описываем систему. И это делает её сильно отличной от других величин, с которыми принято работать в физике.

Классической системой, которую рассматривают в физике, является газ, находящийся в сосуде под поршнем. Микросостояние газа — это положение и импульс (скорость) каждой его молекулы. Это эквивалентно тому, что вы знаете значение, выпавшее на каждой кости в рассмотренном раньше примере. Макросостояние газа описывается такими величинами как давление, плотность, объём, химический состав. Это как сумма значений, выпавших на костях.

Величины, описывающие макросостояние, могут быть связаны друг с другом через так называемое «уравнение состояния». Именно наличие этой связи позволяет, не зная микросостояний, предсказывать, что будет с нашей системой, если начать её нагревать или перемещать поршень. Для идеального газа уравнение состояния имеет простой вид:

p = ρT

хотя вы, скорее всего, лучше знакомы с уравнением Клапейрона — Менделеева pV = νRT — это то же самое уравнение, только с добавлением пары констант, чтобы вас запутать. Чем больше микросостояний отвечают данному макросостоянию, то есть чем больше частиц входят в состав нашей системы, тем лучше уравнение состояния её описывают. Для газа характерные значения числа частиц равны числу Авогадро, то есть составляют порядка 10²³.

Величины типа давления, температуры и плотности называются усреднёнными, поскольку являются усреднённым проявлением постоянно сменяющих друг друга микросостояний, отвечающих данному макросостоянию (или, вернее, близким к нему макросостояниям). Чтобы узнать в каком микросостоянии находится система, нам надо очень много информации — мы должны знать положение и скорость каждой частицы. Количество этой информации и называется энтропией.

Как меняется энтропия с изменением макросостояния? Это легко понять. Например, если мы немного нагреем газ, то скорость его частиц возрастёт, следовательно, возрастёт и степень нашего незнания об этой скорости, то есть энтропия вырастет. Или, если мы увеличим объём газа, отведя поршень, увеличится степень нашего незнания положения частиц, и энтропия также вырастет.

Если мы рассмотрим вместо газа какое-нибудь твёрдое тело, особенно с упорядоченной структурой, как в кристаллах, например, кусок металла, то его энтропия будет невелика. Почему? Потому что зная положение одного атома в такой структуре, вы знаете и положение всех остальных (они же выстроены в правильную кристаллическую структуру), скорости же атомов невелики, потому что они не могут улететь далеко от своего положения и лишь немного колеблются вокруг положения равновесия.

Если кусок металла находится в поле тяготения (например, поднят над поверхностью Земли), то потенциальная энергия каждого атома в металле приблизительно равна потенциальной энергии других атомов, и связанная с этой энергией энтропия низка. Это отличает потенциальную энергию от кинетической, которая для теплового движения может сильно меняться от атома к атому.

Если кусок металла, поднятый на некоторую высоту, отпустить, то его потенциальная энергия будет переходить в кинетическую энергию, но энтропия возрастать практически не будет, потому что все атомы будут двигаться приблизительно одинаково. Но когда кусок упадёт на землю, во время удара атомы металла получат случайное направление движения, и энтропия резко увеличится. Кинетическая энергия направленного движения перейдёт в кинетическую энергию теплового движения. Перед ударом мы приблизительно знали, как движется каждый атом, теперь мы эту информацию потеряли.

Второй закон термодинамики утверждает, что энтропия (замкнутой системы) никогда не уменьшается. Мы теперь можем понять, почему: потому что невозможно внезапно получить больше информации о микросостояниях. Как только вы потеряли некую информацию о микросостоянии (как во время удара куска металла об землю), вы не можете вернуть её назад.

Давайте вернёмся обратно к игральным костям. Вспомним, что макросостояние с суммой 59 имеет очень низкую энтропию, но и получить его не так-то просто. Если бросать кости раз за разом, то будут выпадать те суммы (макросостояния), которым отвечает большее количество микросостояний, то есть будут реализовываться макросостояния с большой энтропией. Самой большой энтропией обладает сумма 35, и именно она и будет выпадать чаще других. Именно об этом и говорит второй закон термодинамики. Любое случайное (неконтролируемое) взаимодействие приводит к росту энтропии, по крайней мере до тех пор, пока она не достигнет своего максимума.
И ещё один пример, чтобы закрепить сказанное. Пусть у нас имеется контейнер, в котором находятся два газа, разделённых расположенной посередине контейнера перегородкой. Назовём молекулы одного газа синими, а другого — красными.

Если открыть перегородку, газы начнут перемешиваться, потому что число микросостояний, в которых газы перемешаны, намного больше, чем микросостояний, в которых они разделены, и все микросостояния, естественно, равновероятны. Когда мы открыли перегородку, для каждой молекулы мы потеряли информацию о том, с какой стороны перегородки она теперь находится. Если молекул было N, то утеряно N бит информации (биты и символы, в данном контексте, это, фактически, одно и тоже, и отличаются только неким постоянным множителем).

Ну и напоследок рассмотрим решение в рамках нашей парадигмы знаменитого парадокса демона Максвелла. Напомню, что он заключается в следующем. Пусть у нас есть перемешанные газы из синих и красных молекул. Поставим обратно перегородку, проделав в ней небольшое отверстие, в которое посадим воображаемого демона. Его задача — пропускать слева направо только красных, и справа налево только синих. Очевидно, что через некоторое время газы снова будут разделены: все синие молекулы окажутся слева от перегородки, а все красные — справа.

Получается, что наш демон понизил энтропию системы. С демоном ничего не случилось, то есть его энтропия не изменилась, а система у нас была закрытой. Получается, что мы нашли пример, когда второй закон термодинамики не выполняется! Как такое оказалось возможно?

Решается этот парадокс, однако, очень просто. Ведь энтропия — это свойство не системы, а нашего знания об этой системе. Мы с вами знаем о системе мало, поэтому нам и кажется, что её энтропия уменьшается. Но наш демон знает о системе очень много — чтобы разделять молекулы, он должен знать положение и скорость каждой из них (по крайней мере на подлёте к нему). Если он знает о молекулах всё, то с его точки зрения энтропия системы, фактически, равна нулю — у него просто нет недостающей информации о ней. В этом случае энтропия системы как была равна нулю, так и осталась равной нулю, и второй закон термодинамики нигде не нарушился.

Но даже если демон не знает всей информации о микросостоянии системы, ему, как минимум, надо знать цвет подлетающей к нему молекулы, чтобы понять, пропускать её или нет. И если общее число молекул равно N, то демон должен обладать N бит информации о системе — но именно столько информации мы и потеряли, когда открыли перегородку. То есть количество потерянной информации в точности равно количеству информации, которую необходимо получить о системе, чтобы вернуть её в исходное состояние — и это звучит вполне логично, и опять же не противоречит второму закону термодинамики.

Энтропия в классической термодинамике — Википедия

Термодинамическая энтропия S{\displaystyle S}, часто именуемая просто энтропией, — физическая величина, используемая для описания термодинамической системы, одна из основных термодинамических величин. Энтропия является функцией состояния и широко используется в термодинамике, в том числе технической (анализ работы тепловых машин и холодильных установок) и химической (расчёт равновесий химических реакций).

Утверждение о существовании энтропии и перечисление её свойств составляют содержание второго и третьего начал термодинамики. Значимость данной величины для физики обусловлена тем, что наряду с температурой её используют для описания термических явлений и термических свойств макроскопических объектов. Качественные представления о термическом состоянии системы связаны с тепловыми ощущениями, выражаемыми понятиями «теплее», «холоднее», «нагрев», «охлаждение», «степень нагретости». К термическим относят свойства, характеризующие поведение вещества при его нагреве или охлаждении: термические коэффициенты, теплоёмкость и другие калорические коэффициенты, постоянную Кюри, показатели термостойкости, пределы огнестойкости и т. д.; примерами термических явлений служат термическое расширение, пироэлектричество, электрокалорический эффект, теплопроводность, изменение агрегатного состояния — кристаллизация и замерзание, плавление и таяние, испарение, кипение, сублимация (возгонка), конденсация и другие процессы.

Понятие энтропии, её обозначение и название были введены Р. Клаузиусом (1865). Абстрактность этого понятия — одного из краеугольных камней термодинамики — и разнообразие подходов к обоснованию существования энтропии как термодинамической величины привели к появлению аксиоматики термодинамики.

Термодинамическая дефиниция энтропии[править | править код]

В термодинамике энтропию вводят, обосновывая её существование, перечисляя её свойства и строя для неё шкалу измерения на основании первого, второго и третьего начал термодинамики.

В термодинамических формализмах Клаузиуса^[1] и Каратеодори^[2] энтропию вводят одновременно с абсолютной термодинамической температурой. Математический аппарат термодинамики Гиббса^[3] основан на использовании энтропии в качестве независимой термодинамической переменной, тогда как температура — естественный кандидат на эту роль, вводится как функция внутренней энергии и энтропии. Наконец, в рациональной термодинамике энтропию выражают через внутреннюю энергию и температуру, которые рассматривают как основные неопределяемые переменные теории.

Энтропия простой системы[править | править код]

Первое начало (закон) термодинамики устанавливает связь между внутренней энергией, работой и теплотой: одна из этих физических величин задаётся с помощью двух других, которые, будучи исходными объектами теории, в рамках самой этой теории определены быть не могут просто потому, что не существует понятий более общих, под которые их можно было бы подвести^[4]. Термодинамика заимствует понятия энергии и работы из других разделов физики^[5][6], тогда как определение количеству теплоты, наоборот, даётся только и именно в термодинамике. Согласно Клаузиусу теплоту Q{\displaystyle Q} определяют через внутреннюю энергию U{\displaystyle U} и работу W{\displaystyle W}^[7][8]. При использовании термодинамического правила знаков^[9] математическое выражение для первого начала термодинамики в формулировке Клаузиуса имеет вид^[10]:

Q≡ΔU−W.{\displaystyle Q\equiv \Delta U-W.}

(Дефиниция теплоты по Клаузиусу)

Первое начало в этой формулировке вводит теплоту как физическую характеристику процесса, поведение которой определяется законом сохранения энергии, но не определяет её как математический объект. Детализировать дефиницию теплоты проще всего для равновесного процесса, когда работу, а следовательно и теплоту, можно выразить через переменные состояния. Для бесконечно малого^[11]равновесного процесса в простой системе^[12] возможен единственный вид работы — работа расширения/сжатия Wv{\displaystyle W_{v}}:

δWv=−PdV,{\displaystyle \delta W_{v}=-PdV,}

(Работа расширения/сжатия для равновесного процесса в простой системе)

где P{\displaystyle P} — давление, V{\displaystyle V} — объём; символ δ{\displaystyle \delta } означает, что соответствующая величина относится к бесконечно малому процессу. Таким образом, для первого начала термодинамики в формулировке Клаузиуса получаем^[13][14]:

δQ=dU+PdV,{\displaystyle \delta Q=dU+PdV,}

(Первое начало для равновесного процесса в простой системе)

где δQ{\displaystyle \delta Q} — элементарная (бесконечно малая) теплота процесса.

Это выражение, определяющее элементарную теплоту как математический объект, есть линейная дифференциальная форма (форма Пфаффа) для двух независимых переменных. Для данной пфаффовой формы условие интегрируемости Эйлера не выполняется, то есть δQ{\displaystyle \delta Q} есть функционал^[15], а не полный дифференциал несуществующей функции Q(U,V){\displaystyle Q(U,V)}^[14]. Из теории дифференциальных форм известно, однако, что если выполняется условие Фробениуса^[16], то пфаффова форма имеет интегрирующий множитель/делитель, превращающий эту форму в полный дифференциал и представляющий из себя функцию тех же независимых переменных, которые входят в форму Пфаффа^[17]. Пфаффовы формы, имеющие интегрирующий множитель/делитель называют голономными; пфаффова форма двух переменных всегда голономна (теорема Коши)^[18][19]. Поэтому для простых равновесных систем существует функция состояния S(U,V){\displaystyle S(U,V)}, полный дифференциал которой равен

dS ≡ δQT = 1TdU + PTdV,{\displaystyle dS~\equiv ~{\frac {\delta Q}{T}}~=~{\frac {1}{T}}dU~+~{\frac {P}{T}}dV,}

(Дефиниция энтропии простой равновесной системы)

где

T=T(U,V){\displaystyle T=T(U,V)}

есть интегрирующий делитель для формы Пфаффа. Клаузиус назвал функцию состояния S{\displaystyle S} энтропией (от греческого ἐντροπία — изменение, превращение, преобразование). Второе начало термодинамики утверждает, что энтропия существует для любых равновесных систем, а не только простых, и что интегрирующий делитель T{\displaystyle T} есть абсолютная термодинамическая температура^{[20][21][22][19]}. Неравновесная термодинамика распространяет представление о локальной энтропии и локальной температуре на любые термодинамические системы.

Интегрирование уравнения для энтропии приводит к появлению в выражении для функции S(U,V){\displaystyle S(U,V)} произвольной постоянной, зависящей от выбора начальной точки отсчёта энтропии. Произвол в выборе начального состояния для энтропии устраняет третий закон термодинамики.

Энтропия закрытой системы в термодинамике Клаузиуса — Каратеодори[править | править код]

Традиционный подход к построению термодинамики (аксиоматика Клаузиуса — Каратеодори) основан на использовании представления о внутренней энергии как базовом понятии теории, заимствовании формул для вычисления термодинамической работы из механики и электродинамики сплошных сред, и первом начале термодинамики в формулировке Клаузиуса.

Помимо работы расширения/сжатия система может одновременно выполнять другие виды работ, например работу изменению площади поверхности раздела фаз, работу перемещения в поле тяготения, работу поляризации диэлектрика в электрическом поле и т. д. Объединяет все эти виды работ формальная структурная идентичность расчётных формул друг с другом и с выражением для работы расширения/сжатия^[23][24][25]:

δWi=Xidxi,{\displaystyle \delta W_{i}=X_{i}dx_{i},}

где δWi{\displaystyle \delta W_{i}} — элементарная работа i{\displaystyle i}-го типа, xi{\displaystyle x_{i}} — обобщённая координата, сопряжённая с обобщённой силой Xi.{\displaystyle X_{i}.} Каждой обобщённой координате соответствует своя обобщённая сила; физические переменные, соответствующие обобщённым координатам и силам, конкретизируют применительно к решаемой задаче^[26][27].

Если однородная система одновременно совершает несколько различных видов работ, то они суммируются и полная работа системы δW{\displaystyle \delta W} равна^[23][28][29]

δW=∑iXidxi,{\displaystyle \delta W=\sum _{i}X_{i}dx_{i},}

(Суммарная работа для равновесного процесса в однородной системе)

а для первого начала термодинамики получаем соотношение^[30][31]:

δQ=dU−∑iXidxi,{\displaystyle \delta Q=dU-\sum _{i}X_{i}dx_{i},}

(Первое начало для равновесного процесса в однородной системе)

которое как и в случае простой системы представляет собой форму Пфаффа. Следствием второго начала термодинамики в любой его формулировке является вывод о том, что пфаффова форма δQ{\displaystyle \delta Q} при любом числе переменных всегда голономна^[21] и, следовательно, для любой закрытой термодинамической системы существуют энтропия

S=S(U,{xi}){\displaystyle S=S(U,\{x_{i}\})}

(Энтропия однородной закрытой системы)

и абсолютная термодинамическая температура

T=T(U,{xi}).{\displaystyle T=T(U,\{x_{i}\}).}

Выражение {xi}{\displaystyle \{x_{i}\}} есть сокращение для перечисления x1,x2,…,xi,…{\displaystyle x_{1},x_{2},…,x_{i},…} переменных определённого типа, в данном случае — обобщённых координат.

Энтропия открытой системы[править | править код]

Принимая, что теплота и работа являются двумя единственно возможными формами передачи энергии^[32][33][34], а изменение энергии, связанное с переносом вещества в открытой системе, есть составная часть общей работы, называемая химической работой (работой перераспределения масс веществ^[35]), в случае однородной открытой системы дифференциальную форму δQ{\displaystyle \delta Q} для закрытой системы следует дополнить слагаемым, учитывающим элементарную химическую работу δZ{\displaystyle \delta Z}^{[36][37][38][39][40]}:

δZ=∑jμjdmj,{\displaystyle \delta Z=\sum _{j}\mu _{j}dm_{j},}

(Химическая работа для равновесного процесса в открытой однородной системе)

где mj{\displaystyle m_{j}} — масса j{\displaystyle j}-го компонента^[41], μj{\displaystyle \mu _{j}} — химический потенциал этого компонента.

Пфаффова форма δQ{\displaystyle \delta Q} для открытой однородной системы равна^[29]

δQ=dU−∑iXidxi−∑jμjdmj.{\displaystyle \delta Q=dU-\sum _{i}X_{i}dx_{i}-\sum _{j}\mu _{j}dm_{j}.}

(Первое начало для равновесного процесса в открытой однородной системе)

Дальнейшие рассуждения о существовании энтропии

S=S(U,{xi},{mj}){\displaystyle S=S(U,\{x_{i}\},\{m_{j}\})}

и абсолютной термодинамической температуры

T=T(U,{xi},{mj}){\displaystyle T=T(U,\{x_{i}\},\{m_{j}\})}

для открытой системы ничем не отличаются от соображений, высказанных при рассмотрении закрытой системы, поэтому ниже перечислены причины, по которым открытые системы потребовали отдельного рассмотрения.

Первая из этих причин состоит в том, что использование в понятийном аппарате термодинамики химической работы как части общей работы делает неэквивалентными представления об адиабатной изоляции как накладывающей запрет на обмен веществом (то есть любая адиабатно изолированная система есть система закрытая или, говоря иначе, масса есть адиабатически заторможенная величина)^{[42][43][44][45]}, и адиабатной изоляции как допускающей обмен энергией только в форме работы^[46][47]. Восстановить эквивалентность приведённых выше формулировок об адиабатной изоляции удаётся, если модифицировать дефиницию теплоты по Клаузиусу, добавив к теплоте и работе третью форму передачи энергии — энергию переноса массы Z{\displaystyle Z}^[48][49]:

Q≡ΔU−W−Z,{\displaystyle Q\equiv \Delta U-W-Z,}

(Модифицированная дефиниция теплоты для открытой системы)

где δZ{\displaystyle \delta Z} задаётся выражением для химической работы.

Вторая причина отдельного рассмотрения вопроса об энтропии открытых систем заключается в следующем. За исключением химического потенциала все входящие в пфаффову форму δQ{\displaystyle \delta Q} для открытой системы переменные в рамках термодинамического формализма представляют собой неопределяемые величины, заимствуемые из других разделов физики, что подразумевает необязательность их описания в самой термодинамике. Химический потенциал вводится в термодинамике и либо должен быть отнесён к базовым неопределяемым понятиям, для которых возможно только пояснительное описание, либо же от термодинамики требуется точная дефиниция химического потенциала. Как неопределяемую величину химический потенциал можно вводить одновременно с температурой и энтропией (более, того П. А. Жилин^[50] считает такой подход единственно правильным^[51]), но традиционно химический потенциал предпочитают вводить в рассмотрение как вторичную переменную на основе предварительно сформированного представления об энтропии открытой системы. Для этого вслед за У. Гиббсом^[52][45] без доказательства принимают утверждение о существовании энтропии открытой системы^[53][54][55]

S=S(U,{xi},{mj}){\displaystyle S=S(U,\{x_{i}\},\{m_{j}\})}

(Энтропия открытой однородной системы по Гиббсу; фундаментальное уравнение Гиббса в энтропийном выражении)

как функции состояния, при неизменности масс компонентов совпадающей с энтропией однородной закрытой системы. Из фундаментального уравнения Гиббса в дифференциальной форме^[55]

dS=1TdU−1T∑iXidxi−1T∑jμjdmj{\displaystyle dS={\frac {1}{T}}dU-{\frac {1}{T}}\sum _{i}X_{i}dx_{i}-{\frac {1}{T}}\sum _{j}\mu _{j}dm_{j}}

(Дифференциальная форма фундаментального уравнения Гиббса для энтропии)

находим значения частных производных энтропии:

(∂S∂U){xi},{mj}=1T,{\displaystyle \left({\frac {\partial S}{\partial U}}\right)_{\{x_{i}\},\{m_{j}\}}={\frac {1}{T}},}

(∂S∂xr)U,{xi≠r},{mj}=−XrT,{\displaystyle \left({\frac {\partial S}{\partial x_{r}}}\right)_{U,\{x_{i\neq r}\},\{m_{j}\}}=-{\frac {X_{r}}{T}},}

(∂S∂V)xi≠V,{mj}=PT.{\displaystyle \left({\frac {\partial S}{\partial V}}\right)_{x_{i}\neq V,\{m_{j}\}}={\frac {P}{T}}.}

Химический потенциал k{\displaystyle k}-го компонента выразим через частную производную энтропии по массе этого компонента^[56]:

μk≡−T(∂S∂mk)U,{xi},{mj≠k}.{\displaystyle \mu _{k}\equiv -T\left({\frac {\partial S}{\partial m_{k}}}\right)_{U,\{x_{i}\},\{m_{j\neq k}\}}.}

(Дефиниция химического потенциала компонента)

Построение теории на основе постулирования существования энтропии как функции состояния, в состав независимых переменных которой входят массы компонентов, составляет главное содержание термодинамики Гиббса^[57], а способ, каким выполнено распространение термодинамики Клаузиуса на открытые системы, позволяет говорить об аксиоматике Гиббса^[52][45]. В термодинамике Гиббса вводят понятия компонента системы, фазы и многофазной гетерогенной системы, постулируют существование внутренней энергии U{\displaystyle U} и энтропии S{\displaystyle S} как аддитивных переменных состояния, постулируют связь этих величин с независимыми переменными состояния в виде фундаментальных уравнений Гиббса в энергетическом и энтропийном выражениях, постулируют аддитивность входящих в эти фундаментальные уравнения независимых переменных, постулируют, что T{\displaystyle T} есть термодинамическая температура, вводят химический потенциал μ{\displaystyle \mu } и постулируют общее условие термодинамического равновесия в системе^[58], рассматриваемое далее в числе свойств энтропии.

Обратите внимание, что содержательную дефиницию температуры по Гиббсу^[59][60][61]

T≡(∂U∂S)V,{xi}{\displaystyle T\equiv \left({\frac {\partial U}{\partial S}}\right)_{V,\{x_{i}\}}}

(Термодинамическая температура по Гиббсу)

можно, с другой стороны, рассматривать и как описательную дефиницию энтропии. А именно, энтропия в термодинамике Гиббса есть такая экстенсивная переменная состояния, что производная внутренней энергии по энтропии представляет собой интенсивную переменную состояния, обладающую всеми положенными термодинамической температуре свойствами.

Энтропия в рациональной термодинамике[править | править код]

Рациональная термодинамика не подразделяет термодинамику на равновесную и неравновесную; обе эти дисциплины рассматриваются как единая часть физики сплошных сред^{[62][63][64][65]}. Равновесная рациональная термодинамика есть результат применения общей теории к системам в состоянии равновесия^[66]. Исходные неопределяемые понятия теории — энергия E{\displaystyle E}, объём V{\displaystyle V} и число молей компонента n{\displaystyle n}. По аналогии с давлением

P=−∂E∂V{\displaystyle P=-{\frac {\partial E}{\partial V}}}

при механическом равновесии имеющем одинаковое значение во всех частях системы, вводят химический потенциал μ{\displaystyle \mu }

μ≡∂E∂n,{\displaystyle \mu \equiv {\frac {\partial E}{\partial n}},}

как интенсивную величину, имеющую при химическом равновесии одно и то же значение во всех частях системы^[67]. Абсолютную термодинамическую температуру вводят посредством следующей аксиомы: существует интенсивная термодинамическая величина, температура

T=T(E,V,n),{\displaystyle T=T(E,V,n),}

которая характеризует степень нагретости тел и обладает следующими свойствами^[68]:

• в выбранном за начало отсчёта состоянии температура равна нулю

TE=0=0{\displaystyle T_{E=0}=0} ;

• температура монотонно растёт с увеличением энергии системы

∂T∂E>0{\displaystyle {\frac {\partial T}{\partial E}}>0} ;

• при термодинамическом равновесии имеет одно и то же значение во всех частях системы.

Энтропию в рациональной термодинамике задают как аддитивную величину, равную^[69]

S(E)≡

Что такое авитаминоз: признаки, симптомы, как избежать

С авитаминозом сталкивается большинство людей, но только часть понимает, в чем корень проблемы. Своевременное лечение помогает избежать ухудшения здоровья, сниженной трудоспособности и плохого настроения.

Что такое авитаминоз?

https://pixabay.com

С пищей организм получает необходимые вещества, минералы и микроэлементы. Когда питание бедное или продукты не содержат требуемого, начинаются проблемы и возникает авитаминоз. И даже сбалансированное питание с достаточным количеством жиров, белков и сложных углеводов не гарантирует здоровья.

Фермерство, при котором для ускоренного роста злаков, фруктов и овощей их удобряют добавками, приводит к дефициту элементов. Человек считает, что получает с фруктами витамины, а их — мизерное количество.

Ситуациях ухудшается, когда солнца мало, овощи и фрукты менее доступные по цене. Авитаминоз распространен на севере, в семьях с низким уровнем дохода и у людей с ограничениями в питании (веганство, вегетарианство, медицинская диета). Также проблема обостряется в осеннее время и весной.

Общие признаки и симптомы

Симптомы легкого авитаминоза слабо заметны. Человеку кажется, что он быстрее устает и стало труднее концентрироваться. Мерзнет в мороз даже в одежде. Но на первой стадии признаки склонны списывать на переутомление, изменение погоды. Люди стараются больше спать, однако это не помогает. А к усталости добавляется апатия или раздражительность.

https://pixabay.com

Появляются и физические признаки: сон хуже, тяжело заснуть или проснуться, учащаются простудные болезни. Волосы секутся, кожа тусклая и сухая, ногти трескаются. Десна кровоточат или у зубов повышается чувствительность к сладкому, соленому, горячему, холодному. В тяжелом случае ухудшается зрение, возникают признаки депрессии.

Если иммунитет сильно снижен, то авитаминоз проявляется прыщами и ранками на коже. Порезы долго заживают. В попытках компенсировать нехватку витаминов, организм повышает аппетит. В результате человек больше ест и набирает вес. Но если пища с низким содержанием витаминов, проблемы дополнительные приемы пищи не решают.

Как избежать

Для компенсации дефицита веществ врачи прописывают витамины. Анализы, которые позволяют определить, чего конкретно не хватает, дорогие. Поэтому доктора часто пропускают фазу анализов и переходят к назначению комплексов. При покупке добавок соблюдают осторожность — если куплена подделка, то эффект окажется нулевым.

Приобретать средства стоит в проверенных аптеках и не вестись на низкую цену. Предупредить приобретение некачественного товара очень легко: упаковка должна быть целой, а срок годности не истекшим. В интернете советуют лечить авитаминоз употреблением овощей и фруктов. Но из-за интенсивного фермерства результата придется ждать долго и не факт, что он появится.

https://pixabay.com

Но это не означает, что фрукты не нужны. Из продуктов питания они всасываются без проблем и редко дают побочные эффекты. А побочные эффекты от аптечных средств — вещь распространенная. И еще, если был курс приема антибиотиков или микрофлора кишечника нарушена из-за другой болезни, придется сначала ее восстановить. Иначе добавки плохо усваиваются и не приносят пользы.

Еще случается, что человек регулярно пьет витамины, но состояние не улучшается. Коварство ситуации в том, что это может быть не авитаминоз, а его полная противоположность — гипервитаминоз. Такое случается, когда человек увлекается добавками.

Чтобы распознать гипервитаминоз, следует провести анализы и посоветоваться с врачом. Вероятно, он посоветует приостановить прием витаминов и посмотреть на самочувствие. И для выбора витаминов тоже желательно обратиться к доктору.

Как энтропия управляет нашей жизнью

Представьте, что вы взяли коробку с пазлом и высыпали все кусочки мозаики на стол. В теории кусочки могут упасть на свои места так, что картинка сразу сложится целиком. Но в жизни так никогда не бывает. Почему?

Потому что шансы на это ничтожно малы, ведь каждый кусочек пазла должен упасть только одним определённым образом, чтобы картина сложилась. С точки зрения математики, вероятность, что это произойдёт случайно, минимальна.

Что такое энтропия

jamesclear.com

Энтропия — это мера неупорядоченности. И она всегда увеличивается со временем. Всё естественным образом стремится к беспорядку. Здания разрушаются. Машины ржавеют. Люди стареют. Даже горы постепенно рассыпаются.

Это правило, известное как второе начало термодинамики, — один из фундаментальных законов нашей Вселенной. Оно гласит, что в изолированной системе энтропия остаётся неизменной или увеличивается (но никогда не уменьшается).

Но не стоит впадать в панику, есть и хорошие новости. Мы можем сопротивляться силам энтропии. Мы можем собрать рассыпавшийся пазл. Прополоть заросший сад. Убраться в захламлённой комнате. Организовать разрозненных людей в сплочённую команду.

Так как Вселенная стремится к беспорядку, нам приходится затрачивать энергию, чтобы создать в своей жизни стабильность и упорядоченность.

Чтобы отношения были успешными, нужны забота и внимание. Чтобы дом был в хорошем состоянии, его нужно ремонтировать и содержать в чистоте. Для успеха команды необходимы общение и сотрудничество. Если не прилагать усилий, всё будет стремиться к распаду.

Этот вывод — что беспорядок со временем всегда увеличивается, и мы можем противостоять этому, затрачивая энергию, — открывает главную цель жизни. Мы должны прилагать усилия, чтобы создавать порядок, который сможет устоять перед неумолимым напором энтропии.

Как энтропия проявляется в нашей жизни

С помощью энтропии можно объяснить многие непонятные и удивительные факты, например:

Почему наша жизнь так необыкновенна

Представьте человеческий организм. Атомы, из которых состоит тело, могли бы сложиться практически в бесконечное количество вариантов и не создать никакой формы жизни. C точки зрения математики, вероятность нашего существования очень мала. И всё-таки мы существуем.

Во Вселенной, где всем заправляет энтропия, наличие жизни с такой чёткой устойчивой организацией поразительно.

Почему нам нравятся искусство и красота

С помощью энтропии можно объяснить, почему искусство и красота кажутся нам такими эстетически привлекательными. Художник создаёт особую форму порядка и симметрии, какую Вселенная, скорее всего, никогда не породила бы самостоятельно. Число красивых комбинаций гораздо меньше общего количества всех комбинаций. Красота — редкость во Вселенной, полной беспорядка. Поэтому симметричное лицо редко и красиво, ведь несимметричных вариантов несравнимо больше.

Почему идеальные для себя условия нужно не найти, а создать

У каждого из нас свои таланты, навыки и интересы. Но общество и культура, в которых мы живём, не создавались специально под нас. Помня об энтропии, подумайте, каковы шансы, что условия, в которых вы выросли, идеальны для раскрытия ваших талантов?

Крайне маловероятно, что жизнь создаст для вас ситуацию, идеально подходящую под ваши способности. Скорее всего, вы окажетесь в положении, не совсем соответствующем вашим навыкам и потребностям.

Мы обычно описываем такое состояние, как «не в своей тарелке», «не в своей стихии». Естественно, в таких условиях гораздо сложнее добиться успеха, принести пользу, победить. Зная это, мы должны сами создавать для себя идеальные условия жизни.

---

Сложности в жизни возникают не потому, что планеты так выстроились, и не потому, что какие-то высшие силы сговорились против вас. Это просто действует закон энтропии. Состояний беспорядка гораздо больше, чем упорядоченных. Учитывая всё это, удивительно не то, что в жизни есть проблемы, а то, что мы можем их разрешать.