Таблица умножения правильная: Фальшивая и правильная таблица умножения | Интересное | Лазарев Сергей Николаевич. Человек будущего – ПРАВИЛЬНАЯ таблица умножения облегчит жизнь вашим детям!

Фальшивая и правильная таблица умножения | Интересное | Лазарев Сергей Николаевич. Человек будущего

Фальшивая и правильная таблица умножения

Понедельник, 09 Июн. 2014

Многие из нас задумывались, а почему в школе мы заучивали (зубрили) таблицу умножения, не проверяя её правильность, и не находили ответа. У большинства учащихся этот вопрос не стоял, нас с «пелёнок» приучали жить на «веру» и вот к чему это привело. При самостоятельном заполнении таблицы умножения построчно сразу становится очевидным что умножение — это всего лишь многоКРАТНОЕ сложение, и соответственно деление — это многоКРАТНОЕ вычитание, поэтому легко приходит понимание принципиальной разницы выражений “на сколько больше/меньше” и “во сколько раз больше/меньше”.

В продолжениии тем:

Зомбирование — это форсированная обработка подсознания человека, благодаря которой он программируется на безоговорочное подчинение приказам своего хозяина. Само зомбирование начинается с детского сада и продолжается на протяжении всей вашей жизни.

Практические методы зомбирования:  нам вдалбливают в голову множество информации.

Все получаемые там знания делятся на:

• бессмысленные
• бесполезные
• вредные
• ошибочные
• устаревшие

Мы должны четко знать, что все слова русов выражаются предложениями. Есть понятие «грамматика русского языка» и понятие «корень слова». Корень слова несет смысл данного выражения и переносит его на функционалы, т.е. на глагол.

Вводим два понятия:

1) сложение;

2) умножение.

Сложение. Чтобы получить результат сложения, что нужно сделать? Сложить. С ЛОЖЬЮ ЖИТЬ.

Умножение. Чтобы получить результат умножения, что нужно сделать? Умножить. УМНО ЖИТЬ.

   

Для многих математика в школе была непонятным и нелюбимым предметом. В большинстве случаев ученики не виноваты, просто их изначально неправильно учили и чем дальше, тем хуже учат. Рассмотрим ситуацию на примере всем известной «таблицы умножения». Есть такой старый анекдот:»Женщина возмущается что очень удобно 5х5=25, 6х6=36 , а вот почему 7х7=49, неужели было трудно 47 сделать?» Очень практичный подход — сделать как ей удобно, а не как правильно. В начальной школе у всех нас «учительница первая моя», которая крайне редко идет против стандарта, действует «как учили», «по учебнику» и в соответствии с «методическими планами».

Творчество и новаторство в этой области выражается в «женских» подходах  — с со стихами и песнями, танцами и бубнами, зверушками и финтифлюшками от всей души с наивным желанием сделать привлекательнее  и «красивше», с твердой уверенностью в том что «дэти, эта нелза понят, эта нужьна проста запомнит»:

Ни о каком абстрактном мышлении здесь не может быть и речи — отвлекает всё, надо напрягаться даже чтобы просто прочитать. Но не будем сурово осуждать всех творцов, они хотели как лучше, а получилось как всегда.

Вместо злобствования попробуем немного поколдовать над всем известным, казалось бы простейшим предметом и последовательно очистить зерна истины от плевел маразма улучшательства.

Для начала убираем лишние краски, картинки, искажения и получаем обычные колонки примеров умножения:

Затем по принципу соблюдения необходимых и достаточных условий, отсекаем лишнее как скульпторы: все примеры умножения на 1 и 10 как элементарные и все повторы. Последнее очень важно, ведь при механическом запоминании следует бойкий ответ 6х8=48, а вот 8х6= уже вызывает заминку либо ошибку. При исключении повторов такое нереально, поскольку уже сама система подачи материала заставляет понять что это одно и то же. Кроме того, психологически облегчает учёбу не только снижение числа примеров со 100 до 36, но и последовательное уменьшение их количества в колонках:

Именно такой, сокращенный вариант (правда с колонкой 1 х …= ) можно было увидеть на обложках школьных тетрадей до 1970-х гг. Несомненно, можно остановиться на этом для удобства механического запоминания, но понимания математики оно не добавит. Поэтому двигаемся дальше.

Внимательный читатель наверное заметил, что до сих пор мы говорили о ПРИМЕРАХ умножения, а не о ТАБЛИЦЕ умножения.

Смотрим как выглядит настоящая, легкая, удобная для запоминания таблица умножения с полным и правильным названием: таблица умножения И ДЕЛЕНИЯ, поскольку множители одновременно являются и делителями. Хорошо заметна симметрия таблицы из-за выделения идущих по диагонали квадратов чисел:

историческое название «таблица Пифагора»

а так выглядела в древности таблица умножения у шумеров:

Делаем последнюю концептуальную трансформацию — начинаем таблицу умножения не сверху, а снизу. Почему? Во-первых, это интуитивно понятнее: ниже — меньше, выше — больше, а направление слева направо сохраняется как совпадающее с направлением письма слева — меньше, затем направо — больше.

Во-вторых … расскажем чуть позднее.

Правильную таблицу умножения можно дать ученику и в готовом виде, но лучше всего если он сам её составит. Да-да. Это вполне доступно даже первокласснику!

Рисуем сетку и нумеруем ряды и столбцы с 1 до 9 — это соответствует примерам умножения на 1, они же будут выполнять функции сомножителя/кратности/во сколько раз.

Затем учеником заполняются ряд и столбец с 2 путем прибавления числа 2 для каждой последующей клеточки, затем ряд и столбец с 3 и так далее, получается простая таблица умножения:

Что это даёт?

Уже с начальной школы ученик привыкает к табличной форме, с которой ему потом придется часто встречаться, интуитивно понимает, что таблицы создаются как удобный и концентрированный справочный материал, часть из которого надо знать наизусть для удобства применения.

Поначалу для удобства пользования таблицей лучше пользоваться «уголком» для выделения строк и столбцов — вырезаем квадрат с одного угла чистого тетрадного листа. Привычка координатного поиска образуется достаточно быстро.

При таком подходе не нужно тупо механически запоминать колонки примеров умножения, а сразу можно дать пользоваться всей таблицей. Пусть она лежит перед глазами в помощь решению примеров и через некоторое время тренировок запоминание придет само, в неё ученик будет заглядывать все реже и реже.

Таблица должна стать тем же, чем она была изначально — помощью в работе. Упор всегда и везде должен быть не на запоминание, а на понимание и знание где можно найти справочный материал и как им пользоваться.

При самостоятельном заполнении таблицы умножения построчно сразу становится очевидным что умножение — это всего лишь многоКРАТНОЕ сложение, и соответственно деление — это многоКРАТНОЕ вычитание, поэтому легко приходит понимание принципиальной разницы выражений «на сколько больше/меньше» и во сколько раз больше/меньше». Это очень важно для последующего составления уравнений по условиям задач.

Выделение штриховкой или цветом диагонали (квадратов чисел) ясно показывает симметричность таблицы, т.е. равнозначность последовательности сомножителей и здесь избыточность материала играет в сторону закрепления его (повторение — мать учения) и самостоятельного выявления такой закономерности.

Уже потом, когда потребуется в процессе обучения, дети узнАют сколько полезного и интересного связано со знакомой с первого класса простенькой табличкой.  Подобно  Журдену из «Мещанина во дворянстве» Ж.Б. Мольера, который с удивлением узнал что он говорит прозой, детям надо будет только добавить новую терминологию и новые выводы. 

Например, им будут говорить уже не просто о втором сомножителе или кратности сложения, а назовут его коэффициентом.

Каждая строка и столбец таблицы представляют из себя арифметическую прогрессию, от которой легко переходим уже к геометрической прогрессии, факториалам и прочим будто бы сложностям.

Если выделить любой прямоугольник на такой таблице, то в правом верхнем углу его будет указана площадь (чудо!), т.е. таким образом демонстрируется что алгебра и геометрия — это всего лишь разные способы отображения общих закономерностей единой науки математики. Другими словами, наглядно показывается что произведение чисел соответствует площади прямоугольника, а квадрат числа — это действительно квадрат (соответственно для куба надо рисовать третью координату). А отсюда легко переходим к решению геометрических задач алгебраическими способами и наоборот — смотря что удобнее.

Понимание графиков с осями Х и Y, названиями «абсцисса» и «ордината» уже не вызовет затруднений — это будет привычная с начальных классов форма представления материала, надо только дорисовать стрелочки. И… объяснить чем отличаются кардинальные числа от ординальных (они же количественные и порядковые соответственно).

В конце-концов и понимание интеграла как суммы бесконечно малых величин исходит именно из понимания сути умножения натуральных чисел (и опять геометрические аналоги — площадь на криволинейной трапеции на графике функции), иначе интегрирование будет тупо восприниматься как заученные механические действия при обнаружении хитрой закорючки в виде длинной буквы S.

Так что большинство проблем из-за НЕПОНИМАНИЯ ОСНОВ.

Разместил(а): Администратор 09/06/2014 в 11:58

Тэги по теме: миф, зомбирование, лженаука, фальсификация науки, математика, таблица умножения, алгебра, геометрия, вычитание, сложение, умножение, суммирование • Российские новости  • Безопасность  • Власть и политика  • Государство и общество  • Женский клуб  • Наука  • Непознанное  • Образование  • Подросткам и детям  • Семья и быт 
• (7) комментариев  • (16050) просмотров  • постоянная ссылка печать | печать комментариев

Комментарии

Чтобы размещать комментарии, вам нужно зарегистрироваться

ПРАВИЛЬНАЯ таблица умножения облегчит жизнь вашим детям!

Экологичное родительство: Вот, когда мои дети учились во втором классе, я отчетливо себе поняла, почему падает уровень математического образования в школе…

Вы же наверняка знаете, что я преподаю математику. А еще вы не раз слышали мнение, что уровень математического образования падает.

Вот, когда мои дети учились во втором классе, я отчетливо себе поняла, почему падает уровень математического образования в школе. Именно во втором классе при закладке самого фундамента математического образования возникает такая гигантская невосполнимая дыра, которую уже никакими костылями в виде калькуляторов не подопрешь.

А именно, главная проблема — в таблице умножения. Посмотрите на тетради в клетку, которые есть у ваших детей-школьников. 

Я долго-долго ходила по магазинам в поисках тетрадей. И все равно, на всех — вот такая картина:

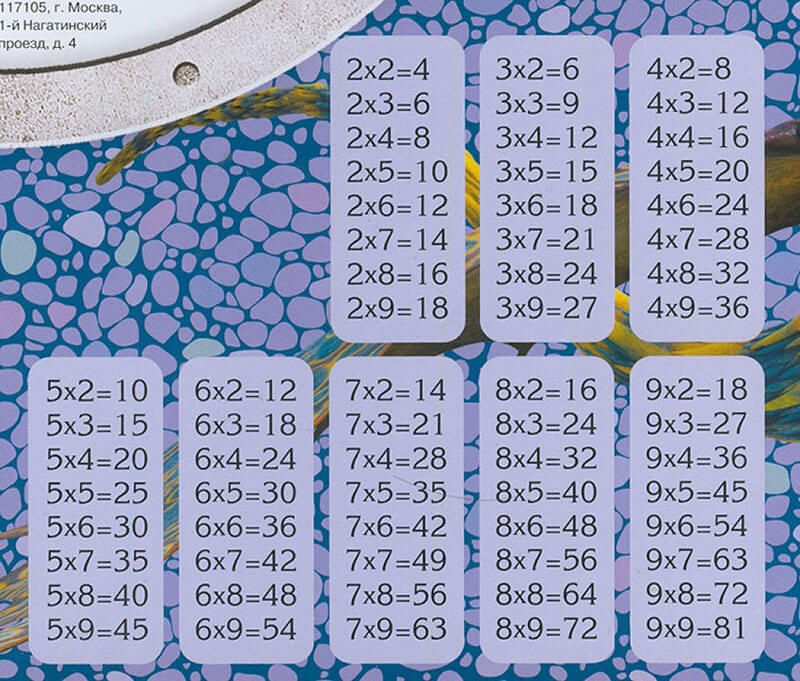
Есть тетради еще хуже (для старшеклассников) на которых таблицы умножения нет, а есть куча бессмысленных формул. 

Ну, так чем же эта тетрадь плоха? Ничего не подозревающий родитель видит, что на тетради таблица умножения. Вроде, всю жизнь же на тетрадях была таблица умножения? Что не так-то?

А проблема как раз в том, что на тетради НЕ таблица умножения. 

Таблица умножения, дорогие мои читатели, это вот:

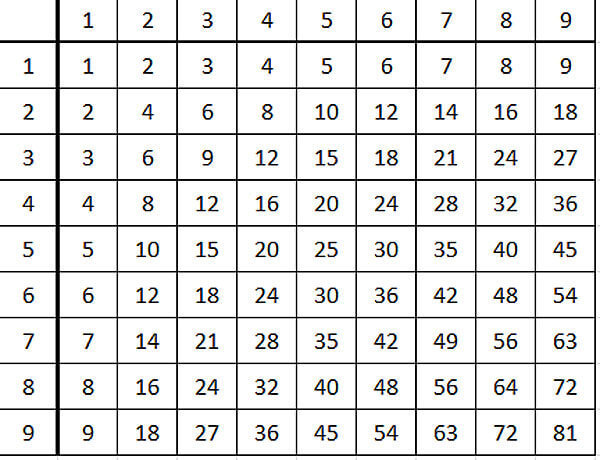
Иногда эту же таблицу даже называют красивым слово «таблица Пифагора». Верхнюю и левую колонки можно не брать, только основной прямоугольник.

Во-первых, это таблица. Во-вторых, она интересная! 

Ни один ребенок в здравом уме не будет рассматривать выписанные столбиками примеры. 

Ни один ребенок, как бы гениален он ни был, не сможет найти в выписанных примерах интересные фишки и закономерности.

Ну, и вообще, когда учитель говорит: «Выучи таблицу умножения», а ребенок даже перед собой таблицы не видит — он сразу понимает, что математика — это такая наука, где обычные вещи названы как-то по-другому и надо много-много зубрить, а понять ничего невозможно. И вообще, надо делать «так, как сказано», а не «так, как есть смысл».

Чем же «таблица» лучше? 

Во-первых, в ней нет мусора и информационного шума в виде левой части примеров. 

Во-вторых, над ней можно подумать. Тут даже нигде не написано, что это умножение — просто таблица.

В-третьих, если она постоянно под рукой и ребенок на нее постоянно натыкается, он волей-неволей начинает запоминать эти числа. В частности, на вопрос «семью восемь» он никогда не ответит 55 — ведь числа 55 вообще в таблице нет и не было! 

Запоминать столбики примеров способны только дети с аномальной памятью. В «таблице» надо запоминать гораздо меньше.

Кроме того, ребенок автоматом ищет закономерности. И сам самостоятельно их находит. Даже такие закономерности находят дети, еще не умеющие умножать.

Например: числа, симметричные относительно диагонали — равны. Понимаете, людской мозг просто настроен искать симметрию, и если ее находит и замечает — очень радуется. А что это означает? Это означает, что от перестановки мест сомножителей произведение не меняется (или что умножение коммутативно, говоря проще).

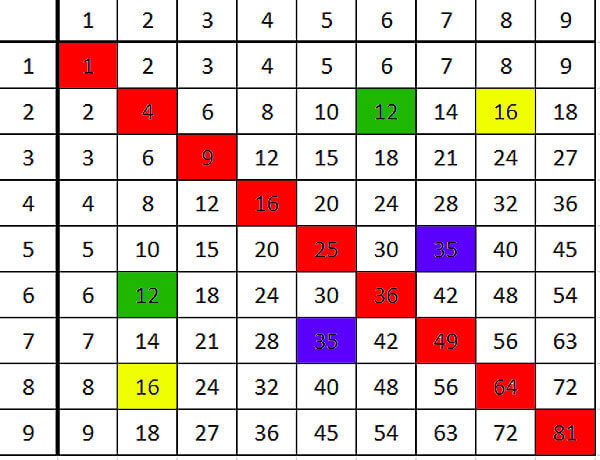
Понимаете, ребенок замечает это сам! А то, что человек придумал сам, он запомнит навсегда, в отличие от того, что он зазубрил или ему сказали.

Помните свой экзамен в вузе по математике? Вы же забыли все теоремы курса, кроме той, что вам досталась, и вам пришлось ее доказывать злобному преподу! Ну, это если вы не списывали, конечно. (Я утрирую, но почти всегда это близко к правде).

А потом ребенок видит, что можно не всю таблицу учить, а только половину. Если мы уже знаем строчку умножения на 3, то нам не надо запоминать «восемь на три», а достаточно вспомнить «три на восемь». Уже вдвое меньше работы. 

А кроме того, очень важно, что ваш мозг не принимает сухую информацию в виде каких-то непонятных столбиков примеров, а думает и анализирует. Т.е. тренируется.

Кроме коммутативности умножения можно заметить, например, еще такой замечательный факт. Если ткнуть в любое число и провести прямоугольник от начала таблицы до этого числа, то количество клеточек в прямоугольнике — ваше число.

И тут умножение уже получает более глубинный смысл, чем просто сокращенная запись нескольких одинаковых слагаемых. Идет смысл и для геометрии — площадь прямоугольника равна произведению его сторон.

А вы не представляете, насколько проще делить с такой таблицей!!! 

Короче, если ваш ребенок во втором классе, распечатайте ему вот такую, правильную, таблицу умножения. Повесьте на стену большую, чтобы он на нее поглядывал, когда делает уроки или сидит за компом. Или еще какой дурью страдает. И напечатайте и заламинируйте ему маленькую (или напишите на картоне). Пусть он ее в школу с собой таскает, и просто удобно под рукой держит (не помешает на такой таблице выделить квадраты по диагонали, чтобы лучше видно).

У моих детей есть — вот такая. И им это реально помогло во втором классе и до сих пор очень сильно помогает на уроках математики.

Вот, честное слово, сразу средний балл по математике увеличится, а ребенок перестанет ныть, что математика тупая. А в придачу, в будущем вашему ребенку тоже будет проще. Он поймет, что надо шевелить мозгами, а не зубрить. И мало, что поймет, он еще и научится это делать.

И повторюсь: в примерах столбиками ничего плохого нет. И количество информации в них содержится такое же, как и в «таблице». Но и ничего хорошего в таких примерах тоже нет. Это — информационный мусор, из которого нужное еще не враз найдешь. опубликовано econet.ru 

Автор: Кукина Екатерина

Также интересно: Демонтаж: реформа нашего образования и спецслужбы США  

Дафна Коллер: Чему нас учит онлайн-образование

P.S. И помните, всего лишь изменяя свое потребление — мы вместе изменяем мир! © econet

Правильная таблица умножения — это просто!)

 Ни о каком абстрактном мышлении здесь не может быть и речи — отвлекает всё, надо напрягаться даже чтобы просто прочитать. Но не будем сурово осуждать всех творцов, они хотели как лучше, а получилось как всегда.

 Вместо злобствования попробуем немного поколдовать над всем известным, казалось бы простейшим предметом и последовательно очистить зерна истины от плевел маразма улучшательства.

 Для начала убираем лишние краски, картинки, искажения и получаем обычные колонки примеров умножения:

 Затем по принципу соблюдения необходимых и достаточных условий, отсекаем лишнее как скульпторы: все примеры умножения на 1 и 10 как элементарные и все повторы. Последнее очень важно, ведь при механическом запоминании следует бойкий ответ 6х8=48, а вот 8х6= уже вызывает заминку либо ошибку. При исключении повторов такое нереально, поскольку уже сама система подачи материала заставляет понять что это одно и то же. Кроме того, психологически облегчает учёбу не только снижение числа примеров со 100 до 36, но и последовательное уменьшение их количества в колонках:

 Именно такой, сокращенный вариант (правда с колонкой 1 х …= ) можно было увидеть на обложках школьных тетрадей до 1970-х гг. Несомненно, можно остановиться на этом для удобства механического запоминания, но понимания математики оно не добавит. Поэтому двигаемся дальше.

 Внимательный читатель наверное заметил, что до сих пор мы говорили о ПРИМЕРАХ умножения, а не о ТАБЛИЦЕ умножения.

 Смотрим как выглядит настоящая, легкая, удобная для запоминания таблица умножения с полным и правильным названием: таблица умножения И ДЕЛЕНИЯ, поскольку множители одновременно являются и делителями. Хорошо заметна симметрия таблицы из-за выделения идущих по диагонали квадратов чисел:

историческое название «таблица Пифагора»

  

а так выглядела в древности таблица умножения у шумеров:

 Делаем последнюю концептуальную трансформацию — начинаем таблицу умножения не сверху, а снизу. Почему? Во-первых, это интуитивно понятнее: ниже — меньше, выше — больше, а направление слева направо сохраняется как совпадающее с направлением письма слева — меньше, затем направо — больше.  Во-вторых … расскажем чуть позднее.

 Правильную таблицу умножения можно дать ученику и в готовом виде, но лучше всего если он сам её составит. Да-да. Это вполне доступно даже первокласснику!

 Рисуем сетку и нумеруем ряды и столбцы с 1 до 9 — это соответствует примерам умножения на 1, они же будут выполнять функции сомножителя/кратности/во сколько раз.

 Затем учеником заполняются ряд и столбец с 2 путем прибавления числа 2 для каждой последующей клеточки, затем ряд и столбец с 3 и так далее, получается простая таблица умножения:

 Что это даёт?

Уже с начальной школы ученик привыкает к табличной форме, с которой ему потом придется часто встречаться, интуитивно понимает, что таблицы создаются как удобный и концентрированный справочный материал, часть из которого надо знать наизусть для удобства применения.

Поначалу для удобства пользования таблицей лучше пользоваться «уголком» для выделения строк и столбцов — вырезаем квадрат с одного угла чистого тетрадного листа. Привычка координатного поиска образуется достаточно быстро.

При таком подходе не нужно тупо механически запоминать колонки примеров умножения, а сразу можно дать пользоваться всей таблицей. Пусть она лежит перед глазами в помощь решению примеров и через некоторое время тренировок запоминание придет само, в неё ученик будет заглядывать все реже и реже.

 Таблица должна стать тем же, чем она была изначально — помощью в работе. Упор всегда и везде должен быть не на запоминание, а на понимание и знание где можно найти справочный материал и как им пользоваться.

  При самостоятельном заполнении таблицы умножения построчно сразу становится очевидным что умножение — это всего лишь многоКРАТНОЕ сложение, и соответственно деление — это многоКРАТНОЕ вычитание, поэтому легко приходит понимание принципиальной разницы выражений «на сколько больше/меньше» и во сколько раз больше/меньше». Это очень важно для последующего составления уравнений по условиям задач.

Выделение штриховкой или цветом диагонали (квадратов чисел) ясно показывает симметричность таблицы, т.е. равнозначность последовательности сомножителей и здесь избыточность материала играет в сторону закрепления его (повторение — мать учения) и самостоятельного выявления такой закономерности.

Уже потом, когда потребуется в процессе обучения, дети узнАют сколько полезного и интересного связано со знакомой с первого класса простенькой табличкой.  Подобно  Журдену из «Мещанина во дворянстве» Ж.Б. Мольера, который с удивлением узнал что он говорит прозой, детям надо будет только добавить новую терминологию и новые выводы.

 Например, им будут говорить уже не просто о втором сомножителе или кратности сложения, а назовут его коэффициентом.

 Каждая строка и столбец таблицы представляют из себя арифметическую прогрессию, от которой легко переходим уже к геометрической прогрессии, факториалам и прочим будто бы сложностям.

 Если выделить любой прямоугольник на такой таблице, то в правом верхнем углу его будет указана площадь (чудо!), т.е. таким образом демонстрируется что алгебра и геометрия — это всего лишь разные способы отображения общих закономерностей единой науки математики. Другими словами, наглядно показывается что произведение чисел соответствует площади прямоугольника, а квадрат числа — это действительно квадрат (соответственно для куба надо рисовать третью координату). А отсюда легко переходим к решению геометрических задач алгебраическими способами и наоборот — смотря что удобнее.

 Понимание графиков с осями Х и Y, названиями «абсцисса» и «ордината» уже не вызовет затруднений — это будет привычная с начальных классов форма представления материала, надо только дорисовать стрелочки. И… объяснить чем отличаются кардинальные числа от ординальных (они же количественные и порядковые соответственно).

 В конце-концов и понимание интеграла как суммы бесконечно малых величин исходит именно из понимания сути умножения натуральных чисел (и опять геометрические аналоги — площадь на криволинейной трапеции на графике функции), иначе интегрирование будет тупо восприниматься как заученные механические действия при обнаружении хитрой закорючки в виде длинной буквы S.

Правильная таблица умножения — офигеть: wod_1958 — LiveJournal

 Ни о каком абстрактном мышлении здесь не может быть и речи — отвлекает всё, надо напрягаться даже чтобы просто прочитать. Но не будем сурово осуждать всех творцов, они хотели как лучше, а получилось как всегда.

 Вместо злобствования попробуем немного поколдовать над всем известным, казалось бы простейшим предметом и последовательно очистить зерна истины от плевел маразма улучшательства.

 Для начала убираем лишние краски, картинки, искажения и получаем обычные колонки примеров умножения:

 Затем по принципу соблюдения необходимых и достаточных условий, отсекаем лишнее как скульпторы: все примеры умножения на 1 и 10 как элементарные и все повторы. Последнее очень важно, ведь при механическом запоминании следует бойкий ответ 6х8=48, а вот 8х6= уже вызывает заминку либо ошибку. При исключении повторов такое нереально, поскольку уже сама система подачи материала заставляет понять что это одно и то же. Кроме того, психологически облегчает учёбу не только снижение числа примеров со 100 до 36, но и последовательное уменьшение их количества в колонках:

 Именно такой, сокращенный вариант (правда с колонкой 1 х …= ) можно было увидеть на обложках школьных тетрадей до 1970-х гг. Несомненно, можно остановиться на этом для удобства механического запоминания, но понимания математики оно не добавит. Поэтому двигаемся дальше.

 Внимательный читатель наверное заметил, что до сих пор мы говорили о ПРИМЕРАХ умножения, а не о ТАБЛИЦЕ умножения.

 Смотрим как выглядит настоящая, легкая, удобная для запоминания таблица умножения с полным и правильным названием: таблица умножения И ДЕЛЕНИЯ, поскольку множители одновременно являются и делителями. Хорошо заметна симметрия таблицы из-за выделения идущих по диагонали квадратов чисел:

историческое название «таблица Пифагора»

  

а так выглядела в древности таблица умножения у шумеров:

 Делаем последнюю концептуальную трансформацию — начинаем таблицу умножения не сверху, а снизу. Почему? Во-первых, это интуитивно понятнее: ниже — меньше, выше — больше, а направление слева направо сохраняется как совпадающее с направлением письма слева — меньше, затем направо — больше.  Во-вторых … расскажем чуть позднее.

 Правильную таблицу умножения можно дать ученику и в готовом виде, но лучше всего если он сам её составит. Да-да. Это вполне доступно даже первокласснику!

 Рисуем сетку и нумеруем ряды и столбцы с 1 до 9 — это соответствует примерам умножения на 1, они же будут выполнять функции сомножителя/кратности/во сколько раз.

 Затем учеником заполняются ряд и столбец с 2 путем прибавления числа 2 для каждой последующей клеточки, затем ряд и столбец с 3 и так далее, получается простая таблица умножения:

 Что это даёт?

Уже с начальной школы ученик привыкает к табличной форме, с которой ему потом придется часто встречаться, интуитивно понимает, что таблицы создаются как удобный и концентрированный справочный материал, часть из которого надо знать наизусть для удобства применения.

Поначалу для удобства пользования таблицей лучше пользоваться «уголком» для выделения строк и столбцов — вырезаем квадрат с одного угла чистого тетрадного листа. Привычка координатного поиска образуется достаточно быстро.

При таком подходе не нужно тупо механически запоминать колонки примеров умножения, а сразу можно дать пользоваться всей таблицей. Пусть она лежит перед глазами в помощь решению примеров и через некоторое время тренировок запоминание придет само, в неё ученик будет заглядывать все реже и реже.

 Таблица должна стать тем же, чем она была изначально — помощью в работе. Упор всегда и везде должен быть не на запоминание, а на понимание и знание где можно найти справочный материал и как им пользоваться.

  При самостоятельном заполнении таблицы умножения построчно сразу становится очевидным что умножение — это всего лишь многоКРАТНОЕ сложение, и соответственно деление — это многоКРАТНОЕ вычитание, поэтому легко приходит понимание принципиальной разницы выражений «на сколько больше/меньше» и во сколько раз больше/меньше». Это очень важно для последующего составления уравнений по условиям задач.

Выделение штриховкой или цветом диагонали (квадратов чисел) ясно показывает симметричность таблицы, т.е. равнозначность последовательности сомножителей и здесь избыточность материала играет в сторону закрепления его (повторение — мать учения) и самостоятельного выявления такой закономерности.

Уже потом, когда потребуется в процессе обучения, дети узнАют сколько полезного и интересного связано со знакомой с первого класса простенькой табличкой.  Подобно  Журдену из «Мещанина во дворянстве» Ж.Б. Мольера, который с удивлением узнал что он говорит прозой, детям надо будет только добавить новую терминологию и новые выводы.

 Например, им будут говорить уже не просто о втором сомножителе или кратности сложения, а назовут его коэффициентом.

 Каждая строка и столбец таблицы представляют из себя арифметическую прогрессию, от которой легко переходим уже к геометрической прогрессии, факториалам и прочим будто бы сложностям.

 Если выделить любой прямоугольник на такой таблице, то в правом верхнем углу его будет указана площадь (чудо!), т.е. таким образом демонстрируется что алгебра и геометрия — это всего лишь разные способы отображения общих закономерностей единой науки математики. Другими словами, наглядно показывается что произведение чисел соответствует площади прямоугольника, а квадрат числа — это действительно квадрат (соответственно для куба надо рисовать третью координату). А отсюда легко переходим к решению геометрических задач алгебраическими способами и наоборот — смотря что удобнее.

 Понимание графиков с осями Х и Y, названиями «абсцисса» и «ордината» уже не вызовет затруднений — это будет привычная с начальных классов форма представления материала, надо только дорисовать стрелочки. И… объяснить чем отличаются кардинальные числа от ординальных (они же количественные и порядковые соответственно).

 В конце-концов и понимание интеграла как суммы бесконечно малых величин исходит именно из понимания сути умножения натуральных чисел (и опять геометрические аналоги — площадь на криволинейной трапеции на графике функции), иначе интегрирование будет тупо восприниматься как заученные механические действия при обнаружении хитрой закорючки в виде длинной буквы S.

Настоящая таблица умножения — Мастерок.жж.рф — LiveJournal

Ну так чем же эта тетрадь плоха? Ничего не подозревающий родитель видит, что на тетради таблица умножения. Вроде всю жизнь на тетрадях была таблица умножения.

Что не так-то? Есть мнение, что это очень вредная таблица умножения, а существует и настоящая.

Вот она …

По-другому ее называют «таблица Пифагора».

Верхнюю и левую колонки можно не брать, только основной прямоугольник. Во-первых, это таблица. Во-вторых, она интересная!
Ни один ребенок не будет рассматривать выписанные столбиками примеры. Ни один ребенок не сможет найти в выписанных примерах интересные фишки и закономерности.

И вообще, когда учитель говорит: «Выучи таблицу умножения», — а ребенок даже перед собой таблицы не видит, он сразу понимает, что математика — это такая наука, где обычные вещи названы по-другому и надо много-много зубрить, а понять ничего невозможно.

Чем же «таблица» лучше?

— Во-первых, в ней нет мусора и информационного шума в виде левой части примеров.

— Во-вторых, над ней можно подумать. Тут даже нигде не написано, что это умножение — просто таблица.

— В-третьих, если она постоянно под рукой и ребенок на нее постоянно натыкается, он волей-неволей начинает запоминать эти числа. В частности, на вопрос «семью восемь» он никогда не ответит «55», ведь числа 55 вообще в таблице нет и не было!

Запоминать столбики примеров способны только дети с аномальной памятью. В «таблице» надо запоминать гораздо меньше.
Кроме того, ребенок автоматом ищет закономерности. И сам самостоятельно их находит. Такие закономерности находят даже дети, еще не умеющие умножать.

Например: числа, симметричные относительно диагонали, равны. Людской мозг просто настроен искать симметрию, и если ее находит и замечает, очень радуется. А что это означает? Это означает, что от перестановки мест сомножителей произведение не меняется.

Понимаете, ребенок замечает это сам! А то, что человек придумал сам, он запомнит навсегда, в отличие от того, что он зазубрил или ему сказали.

А ведь были же и правильные тетради:

Еще что нибудь интересного для вас: замечали ли вы, что с возрастом время летит все быстрее?, а вот Известные фразы, вырванные из контекста. Не забывайте, что «Мертвая» симка дорого обходится и вот Законы, которые защищают вас в магазине и Реальные размеры стран на карте

Это копия статьи, находящейся по адресу http://masterokblog.ru/?p=36153.

Правильная таблица умножения: apxiv — LiveJournal

     Ни о каком абстрактном мышлении здесь не может быть и речи — отвлекает всё, надо напрягаться даже чтобы просто прочитать. Но не будем сурово осуждать всех творцов, они хотели как лучше, а получилось как всегда.

     Вместо злобствования попробуем немного поколдовать над всем известным, казалось бы простейшим предметом и последовательно очистить зерна истины от плевел маразма улучшательства.

     Для начала убираем лишние краски, картинки, искажения и получаем обычные колонки примеров умножения:

     Затем по принципу соблюдения необходимых и достаточных условий, отсекаем лишнее как скульпторы: все примеры умножения на 1 и 10 как элементарные и все повторы. Последнее очень важно, ведь при механическом запоминании следует бойкий ответ 6х8=48, а вот 8х6= уже вызывает заминку либо ошибку. При исключении повторов такое нереально, поскольку уже сама система подачи материала заставляет понять что это одно и то же. Кроме того, психологически облегчает учёбу не только снижение числа примеров со 100 до 36, но и последовательное уменьшение их количества в колонках:

     Именно такой, сокращенный вариант (правда с колонкой 1 х …= ) можно было увидеть на обложках школьных тетрадей до 1970-х гг. Несомненно, можно остановиться на этом для удобства механического запоминания, но понимания математики оно не добавит. Поэтому двигаемся дальше.

     Внимательный читатель наверное заметил, что до сих пор мы говорили о ПРИМЕРАХ умножения, а не о ТАБЛИЦЕ умножения

     Смотрим как выглядит настоящая таблица умножения с полным и правильным названием: таблица умножения И ДЕЛЕНИЯ, поскольку множители одновременно являются и делителями. Хорошо заметна симметрия таблицы из-за выделения идущих по диагонали квадратов чисел

   

        Для сравнения так выглядела в древности таблица умножения у шумеров:

     Делаем последнюю концептуальную трансформацию — начинаем таблицу умножения не сверху, а снизу. Почему? Во-первых, это интуитивно понятнее: ниже — меньше, выше — больше, а направление слева направо сохраняется как совпадающее с направлением письма слева — меньше, затем направо — больше.  Во-вторых … расскажем чуть позднее.

     Правильную таблицу умножения можно дать ученику и в готовом виде, но лучше всего если он сам её составит. Да-да. Это вполне доступно даже первокласснику!

     Рисуем сетку и пронумеровываем ряды и столбцы с 1 до 9 — это соответствует примерам умножения на 1, они же будут выполнять функции сомножителя/кратности/во сколько раз.

     Затем учеником заполняются ряд и столбец с 2 путем прибавления числа 2 для каждой последующей клеточки, затем ряд и столбец с 3 и так далее:

9
8
7
6
5	10	15	20	25
4	8	12	16	20
3	6	9	12	15
2	4	6	8	10	12	14	16	18
1	2	3	4	5	6	7	8	9

     Что это даёт?

    Уже с начальной школы ученик привыкает к табличной форме, с которой ему потом придется часто встречаться, интуитивно понимает, что таблицы создаются как удобный и концентрированный справочный материал, часть из которого надо знать наизусть для удобства применения.

    Поначалу для удобства пользования таблицей лучше пользоваться «уголком» для выделения строк и столбцов — вырезаем квадрат с одного угла чистого тетрадного листа. Привычка координатного поиска образуется достаточно быстро. При таком подходе не нужно тупо механически запоминать колонки примеров умножения, а сразу можно дать пользоваться всей таблицей. Пусть она лежит перед глазами в помощь решению примеров и через некоторое время тренировок запоминание придет само, в нее ученик будет заглядывать все реже и реже

     Таблица должна стать тем же, чем она была изначально — помощью в работе, ведь никому не приходит в голову заставлять учить таблицы Брадиса? Упор всегда и везде должен быть не на запоминание, а на понимание и знание где можно найти справочный материал и как им пользоваться!

     При самостоятельном заполнении таблицы умножения построчно сразу становится очевидным что умножение — это всего лишь многоКРАТНОЕ сложение, и соответственно деление — это многоКРАТНОЕ вычитание, поэтому легко приходит понимание принципиальной разницы выражений «на сколько больше/меньше» и во сколько раз больше/меньше». Это очень важно для последующего составления уравнений по условиям задач.

   Выделение штриховкой или цветом диагонали (квадратов чисел) ясно показывает симметричность таблицы, т.е. равнозначность последовательности сомножителей и здесь избыточность материала играет в сторону закрепления его (повторение — мать учения) и самостоятельного выявления такой закономерности

    Уже потом, когда потребуется в процессе обучения, дети узнАют сколько полезного и интересного связано со знакомой с первого класса простенькой табличкой.  Подобно  Журдену из «Мещанина во дворянстве» Ж.Б. Мольера, который с удивлением узнал что он говорит прозой, детям надо будет только добавить новую терминологию и новые выводы

     Например, им будут говорить уже не просто о втором сомножителе или кратности сложения, а назовут его коэффициентом.

     Каждая строка и столбец таблицы представляют из себя арифметическую прогрессию, от которой легко переходим уже к геометрической прогрессии, факториалам и прочим якобы заумностям.

     Если выделить любой прямоугольник на такой таблице, то в правом верхнем углу его будет указана площадь (чудо!), т.е. таким образом демонстрируется что алгебра и геометрия — это всего лишь разные способы отображения общих закономерностей единой науки математики. Другими словами, наглядно показывается что произведение чисел соответствует площади прямоугольника, а квадрат числа — это действительно квадрат (соответственно для куба надо рисовать третью координату). А отсюда легко переходим к решению геометрических задач алгебраическими способами и наоборот — смотря что удобнее.

     Понимание графиков с осями Х и Y, названиями «абсцисса» и «ордината» уже не вызовет затруднений — это будет привычная с начальных классов форма представления материала, надо только дорисовать стрелочки. И… объяснить чем отличаются кардинальные числа от ординальных (они же количественные и порядковые соответственно).

     В конце-концов и понимание интеграла как суммы бесконечно малых величин исходит именно из понимания сути умножения натуральных чисел (и опять геометрические аналоги — площадь на криволинейной трапеции на графике функции), иначе интегрирование будет тупо восприниматься как заученные механические действия при обнаружении хитрой закорючки в виде длинной буквы S.

     Так что большинство проблем из-за НЕПОНИМАНИЯ ОСНОВ.
источник.

Правильная таблица умножения: aleksa_piter — LiveJournal

   Ни о каком абстрактном мышлении здесь не может быть и речи — отвлекает всё, надо напрягаться даже чтобы просто прочитать. Но не будем сурово осуждать всех творцов, они хотели как лучше, а получилось как всегда.

   Вместо злобствования попробуем немного поколдовать над всем известным, казалось бы простейшим предметом и последовательно очистить зерна истины от плевел маразма улучшательства.

   Для начала убираем лишние краски, картинки, искажения и получаем обычные колонки примеров умножения:

   Затем по принципу соблюдения необходимых и достаточных условий, отсекаем лишнее как скульпторы: все примеры умножения на 1 и 10 как элементарные и все повторы. Последнее очень важно, ведь при механическом запоминании следует бойкий ответ 6х8=48, а вот 8х6= уже вызывает заминку либо ошибку. При исключении повторов такое нереально, поскольку уже сама система подачи материала заставляет понять что это одно и то же. Кроме того, психологически облегчает учёбу не только снижение числа примеров со 100 до 36, но и последовательное уменьшение их количества в колонках:

   Именно такой, сокращенный вариант (правда с колонкой 1 х …= ) можно было увидеть на обложках школьных тетрадей до 1970-х гг. Несомненно, можно остановиться на этом для удобства механического запоминания, но понимания математики оно не добавит. Поэтому двигаемся дальше.

   Внимательный читатель наверное заметил, что до сих пор мы говорили о ПРИМЕРАХ умножения, а не о ТАБЛИЦЕ умножения.

   Смотрим как выглядит настоящая, легкая, удобная для запоминания таблица умножения с полным и правильным названием: таблица умножения И ДЕЛЕНИЯ, поскольку множители одновременно являются и делителями. Хорошо заметна симметрия таблицы из-за выделения идущих по диагонали квадратов чисел:

историческое название «таблица Пифагора»

     

а так выглядела в древности таблица умножения у шумеров:

   Делаем последнюю концептуальную трансформацию — начинаем таблицу умножения не сверху, а снизу. Почему? Во-первых, это интуитивно понятнее: ниже — меньше, выше — больше, а направление слева направо сохраняется как совпадающее с направлением письма слева — меньше, затем направо — больше.  Во-вторых … расскажем чуть позднее.

   Правильную таблицу умножения можно дать ученику и в готовом виде, но лучше всего если он сам её составит. Да-да. Это вполне доступно даже первокласснику!

   Рисуем сетку и нумеруем ряды и столбцы с 1 до 9 — это соответствует примерам умножения на 1, они же будут выполнять функции сомножителя/кратности/во сколько раз.

   Затем учеником заполняются ряд и столбец с 2 путем прибавления числа 2 для каждой последующей клеточки, затем ряд и столбец с 3 и так далее, получается простая таблица умножения:

   Что это даёт?

  Уже с начальной школы ученик привыкает к табличной форме, с которой ему потом придется часто встречаться, интуитивно понимает, что таблицы создаются как удобный и концентрированный справочный материал, часть из которого надо знать наизусть для удобства применения.

  Поначалу для удобства пользования таблицей лучше пользоваться «уголком» для выделения строк и столбцов — вырезаем квадрат с одного угла чистого тетрадного листа. Привычка координатного поиска образуется достаточно быстро.

 При таком подходе не нужно тупо механически запоминать колонки примеров умножения, а сразу можно дать пользоваться всей таблицей. Пусть она лежит перед глазами в помощь решению примеров и через некоторое время тренировок запоминание придет само, в неё ученик будет заглядывать все реже и реже.

   Таблица должна стать тем же, чем она была изначально — помощью в работе. Упор всегда и везде должен быть не на запоминание, а на понимание и знание где можно найти справочный материал и как им пользоваться.

   При самостоятельном заполнении таблицы умножения построчно сразу становится очевидным что умножение — это всего лишь многоКРАТНОЕ сложение, и соответственно деление — это многоКРАТНОЕ вычитание, поэтому легко приходит понимание принципиальной разницы выражений «на сколько больше/меньше» и во сколько раз больше/меньше». Это очень важно для последующего составления уравнений по условиям задач.

 Выделение штриховкой или цветом диагонали (квадратов чисел) ясно показывает симметричность таблицы, т.е. равнозначность последовательности сомножителей и здесь избыточность материала играет в сторону закрепления его (повторение — мать учения) и самостоятельного выявления такой закономерности.

  Уже потом, когда потребуется в процессе обучения, дети узнАют сколько полезного и интересного связано со знакомой с первого класса простенькой табличкой.  Подобно  Журдену из «Мещанина во дворянстве» Ж.Б. Мольера, который с удивлением узнал что он говорит прозой, детям надо будет только добавить новую терминологию и новые выводы.

   Например, им будут говорить уже не просто о втором сомножителе или кратности сложения, а назовут его коэффициентом.

   Каждая строка и столбец таблицы представляют из себя арифметическую прогрессию, от которой легко переходим уже к геометрической прогрессии, факториалам и прочим будто бы сложностям.

   Если выделить любой прямоугольник на такой таблице, то в правом верхнем углу его будет указана площадь (чудо!), т.е. таким образом демонстрируется что алгебра и геометрия — это всего лишь разные способы отображения общих закономерностей единой науки математики. Другими словами, наглядно показывается что произведение чисел соответствует площади прямоугольника, а квадрат числа — это действительно квадрат (соответственно для куба надо рисовать третью координату). А отсюда легко переходим к решению геометрических задач алгебраическими способами и наоборот — смотря что удобнее.

   Понимание графиков с осями Х и Y, названиями «абсцисса» и «ордината» уже не вызовет затруднений — это будет привычная с начальных классов форма представления материала, надо только дорисовать стрелочки. И… объяснить чем отличаются кардинальные числа от ординальных (они же количественные и порядковые соответственно).

   В конце-концов и понимание интеграла как суммы бесконечно малых величин исходит именно из понимания сути умножения натуральных чисел (и опять геометрические аналоги — площадь на криволинейной трапеции на графике функции), иначе интегрирование будет тупо восприниматься как заученные механические действия при обнаружении хитрой закорючки в виде длинной буквы S.