Задание №1. Перевод из одной системы счисления в другую
Автор материалов — Лада Борисовна Есакова.
Системы счисления и их разновидности.
Система счисления – это способ представления, записи чисел с помощью письменных знаков. Количество этих самых знаков (цифр), используемых для записи чисел, называется основанием системы счисления.
Различных систем счисления у разных народов существовало великое множество. Но все их можно поделить на непозиционные и позиционные. Позиционные системы в свою очередь подразделяются на однородные и смешанные.
1. Непозиционные системы счисления.
В непозиционных системах счисления число, обозначаемое цифрой, не зависит от положения цифры в записи числа.
Самым простым примером непозиционной системы счисления является единичная (унарная) система счисления. Это запись числа с помощью повторения зарубок на дощечке или узелков на веревке. Все зарубки, узелки или другие «цифры» абсолютно одинаковы, а потому их порядок не имеет значения, число получается простым суммированием количества символов.


Унарной системой счисления до сих пор пользуются маленькие дети, показывая количество на пальцах.
Еще одной используемой до сих пор почти непозиционной системой счисления является Римская:
Она названа почти непозиционной, потому что в Римской системе, кроме обычного сложения цифр в числе, действует правило: если младшая цифра стоит слева от старшей, она вычитается из суммы.
Т.е. число , а число
Непозиционных систем счисления известно очень много, но мы завершим на этом их рассмотрение. Использование непозиционных систем неудобно, а для очень больших чисел практически невозможно, и к тому же нет возможности записать дроби.
2. Позиционные системы счисления.
В позиционных системах счисления число, обозначаемое цифрой, зависит от положения цифры в записи числа.
Самой популярной позиционной системой является, конечно же, десятичная.
Мы видим, что числа 15 и 51 имеют совсем разные значения, хотя состоят из одних и тех же цифр. Разница обусловлена положением цифры в числе.
Но десятичная система ничем не лучше и не хуже другой позиционной системы, она просто привычная. Число 10 выбрано основанием по количеству пальцев на двух руках (для удобства счета). Однако, в Китае популярной была пятиречная система счисления (по количеству пальцев на одной руке), а двадцатиричная система использовалась у Ацтеков, Майя и некоторых народов Африки (по количеству пальцев на ногах и руках).
Еще одной известной позиционной системой счисления является двенадцатиричная (считали фаланги пальцев (кроме большого) на руке. Элементы двенадцатиричной системы сохранились в Англии: 1 фут = 12 дюймов, 1 шиллинг = 12 пенсов.

Ну и, наконец, незаменимая в наш компьютерный век двоичная система. Почему именно двоичная? Да потому что у компьютера только 2 «пальца», точнее два состояния: «есть ток», «нет тока».
2.1. Однородные системы счисления.
В однородной системе в каждой позиции числа может находиться любая цифра. Примером может быть запись числа в любой позиционной системе счисления (десятичной, двоичной и пр.). Т.е. когда мы пишем число в десятичной системе, в любой позиции мы можем написать цифру от 0 до 9.
2.2. Смешанные системы счисления.
В смешанной системе счисления набор используемых цифр может отличаться в зависимости от позиции. В качестве примера удобно рассмотреть запись времени в формате ЧЧ.ММ.СС (часы.минуты.секунды). В качестве часов может быть использовано число от 00 до 23, в качестве минут и секунд – число от 00 до 59.

Системы счисления. Перевод из одной системы в другую.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2.
Переведем десятичное число 672 в восьмеричную систему счисления.
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т.е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| B | |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Десятичные дроби и смешанные числа в разных системах счисления.
Автор — Лада Борисовна Есакова.
Перевод целых чисел из одной системы счисления в другую обычно не вызывает проблем. А вот необходимость перевести десятичную дробь или смешанное число (число с целой и дробной частью) из системы в систему часто ставит в тупик даже сильных учеников.
1. Перевод смешанного числа в десятичную систему счисления из любой другой.
Для перевода смешанного числа в десятичную систему из любой другой следует пронумеровать разряды числа, начиная с нуля, справа налево от младшего целого разряда. Разряды дробной части нумеруются слева направо от -1 в убывающем порядке. Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.
Пример 1.
Переведите число 105,4 из восьмеричной системы в десятичную.
Решение:
Пронумеруем целые разряды числа справа налево от 0, дробные – слева направо от -1 :

Посчитаем сумму произведений цифр числа на 8 (основание системы) в степени разряда числа:
Ответ:
2. Перевод десятичных дробей из десятичной системы счисления в любую другую.
Для перевода десятичной дроби из десятичной системы в любую другую следует умножать дробь, а затем дробные части произведений, на основание новой системы пока дробная часть не станет равной 0 или до достижения указанной точности. Затем целые части выписать, начиная с первой.
Пример 2
Переведите десятичное число 0,816 в двоичную систему с точностью до сотых.
Решение:
Умножаем дробь 0,816, а затем дробную часть произведения (0,632) на 2 и выписываем целые части, начиная с первой:

Ответ:
Пример 3.
Переведите десятичное число 0,8125 в восьмеричную систему.
Решение:
Умножаем дробь 0,8125, а затем дробную часть произведения (0,5) на 8 и выписываем целые части, начиная с первой:

Ответ:
3. Перевод смешанных чисел из десятичной системы счисления в любую другую
Если необходимо перевести смешанное число из десятичной системы в любую другую, следует перевести целую и дробную части, а затем записать, разделив десятичной запятой.
Пример 4.
Сколько единиц в двоичной записи десятичного числа 14,125?
Решение:
Переведем целую часть числа в двоичную систему:

Переведем дробную часть числа в двоичную систему:

Соединим целую и дробную части:
14,12510 = 1110,0012
Количество единиц равно 4.
Ответ: 4
Ты нашел то, что искал? Поделись с друзьями!
Лекция по информатике на тему «Перевод информации в различные системы счисления»
Урок 7 Тема 2.2. Перевод информации в различные системы счисления
Тема Перевод информации в различные системы счисления
Решение задач по переводу из десятичной в двоичную систему счисления.
Перевод из двоичной системы счисления в восьмеричную, десятичную, шестнадцатеричную.
План урока:
Объяснение темы преподавателем,
Решение студентами примеров с объяснением у доски
Ответы на контрольные вопросы
Перевод из 10-ой в 2-ю систему:
1 способ деления
122 10 =? 2
122 ∟2
12 61∟2
_2 6 30∟2
2 1 15 15∟2
0 0 14 7∟2
1 6 3∟2
1 2 1∟2
1 0 0
1
Ответ:122 10 = 1111010 2
122 ÷ 2 = 61 0 — остаток
61 ÷ 2 = 30 1
30 ÷ 2 = 15 0
15 ÷ 2 = 7 1
7 ÷ 2 = 3 1
3 ÷ 2 = 1 1
1 ÷ 2 = 0 1
Ответ:122 10 = 1111010 2
2 способ разложения по степеням
122 10 =? 2
122= 64 + 32 + 16 + 8 + 2
26 25 24 23 21
1 1 1 1 0 1 02
Ответ:122 10 = 1111010 2
Перевод из 2-ой в 10-ю систему:
11001011 2 =? 10
7 6 5 4 3 2 1 0
11001011 2 = 1×27 + 1×26 + 0×25 + 0×24 +1×23 + 0×22 +1×21 + 1×20 =
1×27 + 1×26 + 1×23 +1×21 + 1×20 = 128 + 64 + 8 + 2 + 1 = 20310
Ответ:11001011 2 =203 10
Контрольные вопросы:
Что называется системой счисления?
Система счисления – это система отображения любого числа с помощью ограниченного количества условных знаков, называемых цифрами.
Какое различие между понятиями «цифра» и «число»?
Число — это абстрагированная от конкретики запись количества (например, число 25 — это двадцать пять предметов чего угодно и не только предметов, а, скажем, лет или килограммов), а цифра — это специальный знак для обозначения количества единиц, символ
Чем отличается позиционная от непозиционной системы счисления?
Непозиционная —каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.
Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе.
Имеется десятичное число 453. Какой вес имеет каждая позиция?
453 — Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3.
Какова минимальная единица измерения информации?
Бит
Назовите производные от бита единицы измерения информации?
1 байт = 23 = 8 бит
1 Килобайт (Кбайт) = 1024 байт = 210 байт
1 Мегабайт (Мбайт) = 210 Кбайт =1024 Кбайт = 220 байт
1 Гигабайт (Гбайт) = 210 Мбайт = 1024 Мбайт = 230 байт
1 Терабайт (Тбайт) = 210 Гбайт = 1024 Гбайт = 240 байт
1 Петабайт (Пбайт) = 210 Тбайт = 1024 Тбайт = 250 байт
Приведите примеры позиционной системы счисления.
Десятичная система счисления, двоичная система счисления, восьмеричная система счисления, шестнадцатеричная система счисления
Какая система счисления является основной системой представления информации в памяти компьютера?
Двоичная система счисления является основной системой представления информации в памяти компьютера.
Перевести из двоичной в десятичную систему счисления:
10012 = ? 10
3 2 1 0
1001 2 = 1×23 + 0×22 + 0×21 + 1×20 = 8 + 1 = 910
1000012 = ? 10
5 4 3 2 1 0
100001 2 = 1×25 + 0×24 +0×23 + 0×22 +0×21 + 1×20 = 32 + 1 = 3310
111012 = ? 10
4 3 2 1 0
11101 2 = 1×24 +1×23 + 1×22 +0×21 + 1×20 = 16 + 8 + 4 + 1= 2910
Перевести из десятичной в двоичную систему счисления:
2510 = ? 2 3810 = ? 2 4710 = ? 6
8110 = ? 2 6010 = ? 2 13610 = ? 8
10210 = ? 2 8210 = ? 2
22110 = ? 2
2510 = ? 2
| 1. |
Запись чисел в восьмеричной системе счисления
Сложность: лёгкое |
1 |
| 2. |
Основные понятия
Сложность: лёгкое |
1 |
| 3. |
Основание
Сложность: лёгкое |
1 |
| 4. |
Восьмеричная система счисления
Сложность: среднее |
2 |
| 5. |
Развёрнутая запись числа
Сложность: среднее |
2 |
| 6. |
Шестнадцатеричная система счисления
Сложность: среднее |
2 |
| 7. |
Системы счисления
Сложность: сложное |
3 |
| 8. |
Двоичная арифметика (сложение)
Сложность: сложное |
3 |
| 9. |
Десятичное число
Сложность: сложное |
3 |
Доклад по математике «Системы счисления»
Доклад на тему:
Системы счисления
(позиционная и непозиционная)
СИСТЕМЫ СЧИСЛЕНИЯ
СИСТЕМЫ СЧИСЛЕНИЯ (нумерация) – совокупность способов обозначения натуральных чисел.
На ранних ступенях развития общества люди почти не умели считать. Они различали совокупности двух и трех предметов; всякая совокупность, содержавшая бóльшее число предметов, объединялась в понятии «много». Предметы при счете сопоставлялись обычно с пальцами рук и ног. По мере развития цивилизации потребность человека в счете стала необходимой. Первоначально натуральные числа изображались с помощью некоторого количества черточек или палочек, затем для их изображения стали использовать буквы или специальные знаки. В древнем Новгороде использовалась славянская система, где применялись буквы славянского алфавита; при изображении чисел над ними ставился знак ~ (титло).
Древние римляне пользовались нумерацией, сохраняющейся до настоящего времени под именем «римской нумерации», в которой числа изображаются буквами латинского алфавита. Сейчас ею пользуются для обозначения юбилейных дат, нумерации некоторых страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т.д. В позднейшем своем виде римские цифры выглядят так:
I = 1; V = 5; X = 10; L = 50; С = 100; D = 500; M = 1000.
О происхождении римских цифр достоверных сведений нет. Цифра V могла первоначально служить изображением кисти руки, а цифра Х могла составиться из двух пятерок. В римской нумерации явственно сказываются следы пятеричной системы счисления. Все целые числа (до 5000) записываются с помощью повторения вышеприведенных цифр. При этом, если бóльшая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед бóльшей (в этом случае она не может повторяться), то меньшая вычитается из бóльшей). Например, VI = 6, т.е. 5 + 1, IV = 4, т.е. 5 – 1, XL = 40, т е. 50 – 10, LX = 60, т.е. 50 + 10. Подряд одна и та же цифра ставится не более трех раз: LXX = 70; LXXX = 80; число 90 записывается ХС (а не LXXXX).
Первые 12 чисел записываются в римских цифрах так:
I, II, III, IV, V, VI, VII, VIII. IX, X, XI, XII.
Другие же числа записываются, например, как:
XXVIII = 28; ХХХIХ = 39; CCCXCVII = 397; MDCCCXVIII = 1818.
Выполнение арифметических действий над многозначными числами в этой записи очень трудно. Тем не менее, римская нумерация преобладала в Италии до 13 в., а в других странах Западной Европы – до 16 в.
В славянской системе нумерации для записи чисел использовались все буквы алфавита, правда, с некоторым нарушением алфавитного порядка. Различные буквы означали различное количество единиц, десятков и сотен. Например, число 231 записывалось в виде ~ СЛА (C – 200, Л – 30, А – 1).
Этим системам свойственны два недостатка, которые привели к их вытеснению другими: необходимость большого числа различных знаков, особенно для изображения больших чисел, и, что еще важнее неудобство выполнения арифметических операций.
Более удобной и общепринятой и наиболее распространенной является десятичная система счисления, которая была изобретена в Индии, заимствована там арабами и затем через некоторое время пришла в Европу. В десятичной системе счисления основанием является число 10.
Существовали системы исчисления и с другими основаниями. В Древнем Вавилоне, например, применялась шестидесятеричная система счисления. Остатки ее мы находим в сохранившемся до сих пор делении часа или градуса на 60 минут, а минуты – на 60 секунд.
Широкое распространение имела в древности и двенадцатеричная система, происхождение которой, вероятно, связано, как и десятичной системы, со счетом на пальцах: за единицу счета принимались фаланги (отдельные суставы) четырех пальцев одной руки, которые при счете перебирались большим пальцем той же руки. Остатки этой системы счисления сохранились и до наших дней и в устной речи, и в обычаях. Хорошо известно, например, название единицы второго разряда – числа 12 – «дюжина». Сохранился обычай считать многие предметы не десятками, а дюжинами, например, столовые приборы в сервизе или стулья в мебельном гарнитуре. Название единицы третьего разряда в двенадцатеричной системе – гросс – встречается теперь редко, но в торговой практике начала столетия оно еще бытовало. Например, в написанном в 1928 стихотворенииПлюшкин В.В.Маяковский, высмеивая людей, скупающих все подряд, писал: «…укупил двенадцать гроссов дирижерских палочек». У ряда африканских племен и в Древнем Китае была употребительна пятеричная система счисления. В Центральной Америке (у древних ацтеков и майя) и среди населявших Западную Европу древних кельтов была распространена двадцатеричная система. Все они также связаны со счетом на пальцах.
Самой молодой системой счисления по праву можно считать двоичную. Эта система обладает рядом качеств, делающей ее очень выгодной для использования в вычислительных машинах и в современных компьютерах.
Позиционные и непозиционные системы счисления.
Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером непозиционной системы счисления является римская система, в которой в качестве цифр используются латинские буквы.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе называется позицией. Первая известная нам система, основанная на позиционном принципе – шестидесятeричная вавилонская. Цифры в ней были двух видов, одним из которых обозначались единицы, другим – десятки.
Однако наиболее употребительной оказалась индо-арабская десятичная система. Индийцы первыми использовали ноль для указания позиционной значимости величины в строке цифр. Эта система получила название десятичной, так как в ней десять цифр.
Различие между позиционой и непозиционной систем счисления легче всего понять на примере сравнения двух чисел. В позиционной системе счисления сравнение двух чисел происходит следующим образом: в рассматриваемых числах слева направо сравниваются цифры, стоящие в одинаковых позициях. Бóльшая цифра соответствует бóльшему значению числа. Например, для чисел 123 и 234, 1 меньше 2, поэтому число 234 больше, чем число 123. В непозиционной системе счисления это правило не действует. Примером этого может служить сравнение двух чисел IX и VI. Несмотря на то, что I меньше, чем V, число IX больше, чем число VI.
Позиционные системы счисления.
Основание системы счисления, в которой записано число, обычно обозначается нижним индексом. Например, 5557 – число, записанное в семеричной системе счисления. Если число записано в десятичной системе, то основание, как правило, не указывается. Основание системы – это тоже число, и его мы будем указывать в обычной десятичной системе. Вообще, число x может быть представлено в системе с основанием p, как x = an·pn +an – 1·pn–1 + a1·p1 + a0·p0, где an…a0 – цифры в представлении данного числа. Так, например,
103510=1·103 + 0·102 + 3·101 + 5·100;
10102 = 1·23 + 0·22 + 1·21 + 0·20 = 10.
Наибольший интерес при работе на ЭВМ представляют системы счисления с основаниями 2, 8 и 16. Вообще говоря, этих систем счисления обычно хватает для полноценной работы как человека, так и вычислительной машины, однако иногда в силу различных обстоятельств все-таки приходится обращаться к другим системам счисления, например к троичной, семеричной или системе счисления по основанию 32.
Чтобы оперировать с числами, записанными в таких нетрадиционных системах, нужно иметь в виду, что принципиально они ничем не отличаются от привычной десятичной. Сложение, вычитание, умножение в них осуществляется по одной и той же схеме.
Почему же не используются другие системы счисления? В основном, потому, что в повседневной жизни люди привыкли пользоваться десятичной системой счисления, и не требуется никакая другая. В вычислительных же машинах используется двоичная система счисления, так как оперировать числами, записанными в двоичном виде, довольно просто.
Часто в информатике используют шестнадцатеричную систему, так как запись чисел в ней значительно короче записи чисел в двоичной системе. Может возникнуть вопрос: почему бы не использовать для записи очень больших чисел систему счисления, например по основанию 50? Для такой системы счисления необходимы 10 обычных цифр плюс 40 знаков, которые соответствовали бы числам от 10 до 49 и вряд ли кому-нибудь понравится работать с этими сорока знаками. Поэтому в реальной жизни системы счисления по основанию, большему 16, практически не используются.
Перевод чисел из одной системы счисления в другую.
Наиболее часто встречающиеся системы счисления – это двоичная, шестнадцатеричная и десятичная. Как же связаны между собой представления числа в различных системах счисления? Есть различные способы перевода чисел из одной системы счисления в другую на конкретных примерах.
Пусть нужно перевести число 567 из десятичной в двоичную систему. Сначала определяется максимальная степень двойки, такая, чтобы два в этой степени было меньше или равно исходному числу. В данном случае это 9, т.к. 29 = 512, а 210 = 1024, что больше начального числа. Таким образом получается число разрядов результата, оно равно 9 + 1 = 10, поэтому результат будет иметь вид 1ххххххххх, где вместо х могут стоять любые двоичные цифры. Вторая цифра результата находится так – двойка возводится в степень 9 и вычитается из исходного числа: 567 – 29 = 55. Остаток сравнивается с числом 28 = 256. Так как 55 меньше 256, то девятый разряд – нуль, т.е. результат имеет вид 10хххххххх. Рассмотрим восьмой разряд. Так как 27 = 128 > 55, то и он будет нулевым.
Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 25 = 32 < 55, поэтому шестой разряд равен 1 (результат 10001ххххх). Для остатка 55 – 32 = 23 справедливо неравенство 24 = 16 < 23, что означает равенство единице пятого разряда. Аналогично получается в результате число 1000110111. Это число разлагается по степеням двойки:
567 = 1·29 + 0·28 + 0·27 + 0·26 + 1·25 + 1·24 + 0·23 + 1·22 + 1·21 + 1·20
При другом способе перевода чисел используется операция деления в столбик. Если взять то же число 567 и разделить его на 2, получается частное 283 и остаток 1. Та же операция производится и с числом 283. Частное – 141, остаток – 1. Опять полученное частное делится на 2 и так до тех пор, пока частное не станет меньше делителя. Теперь, чтобы получить число в двоичной системе счисления, достаточно записать последнее частное, т.е. 1, и приписать к нему в обратном порядке все полученные в процессе деления остатки.
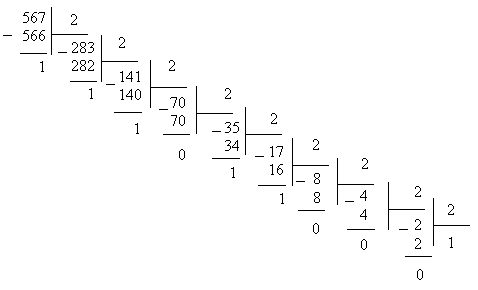
Результат, естественно, не изменился: 567 в двоичной системе счисления записывается как 1 000 110 111.
Эти два способа применимы при переводе числа из десятичной системы в систему с любым основанием. Например, при переводе числа 567 в систему счисления с основанием 16 число сначала разлагается по степеням основания. Искомое число состоит из трех цифр, т.к. 162 = 256 < 567 < 163 = 4096. Определяется цифра старшего разряда. 2·162 = 512 < 567 < 3·162 = 768, следовательно, искомое число имеет вид 2хх, где вместо х могут стоять любые шестнадцатеричные цифры. Остается распределить по следующим разрядам число 55 (567 – 512). 3·16 = 48 < 55 < 4·16 = 64, значит во втором разряде находится цифра 3. Последняя цифра равна 7 (55 – 48). Искомое шестнадцатеричное число равно 237.
Второй способ состоит в последовательном делении в столбик, с единственным отличием в том, что делить надо не на 2, а на 16, и процесс деления заканчивается, когда частное становится строго меньше 16.
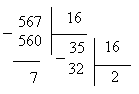
Конечно, для записи числа в шестнадцатеричной системе счисления, необходимо заменить 10 на A, 11 на B и так далее.
Операция перевода в десятичную систему выглядит гораздо проще, так как любое десятичное число можно представить в виде x = a0·pn + a1·pn–1 +… + an–1·p1 + an·p0, где a0 … an – это цифры данного числа в системе счисления с основанием p.
Например,так можно перевести число 4A3F в десятичную систему. По определению, 4A3F= 4·163 + A·162 + 3·16 + F. При замене A на 10, а F на 15, получается 4·163 + 10·162 + 3·16 + 15= 19007.
Проще всего переводить числа из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот. Для того чтобы целое двоичное число записать в системе счисления с основанием 2n, нужно данное двоичное число разбить справа налево на группы по n-цифр в каждой; если в последней левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов; рассмотреть каждую группу, как n-разрядное двоичное число, и заменить ее соответствующей цифрой в системе счисления с основанием 2n.
Таблица 1. Двоично-шестнадцатеричная таблица
Таблица 1. ДВОИЧНО-ШЕСТНАДЦАТЕРИЧНАЯ ТАБЛИЦА
2-ная
0000
0001
0010
0011
0100
0101
0110
0111
16-ная
0
1
2
3
4
5
6
7
2-ная
1000
1001
1010
1011
1100
1101
1110
1111
16-ная
8
9
A
B
C
D
E
F
Таблица 2. Двоично-восьмеричная таблица
Таблица 2. ДВОИЧНО-ВОСЬМЕРИЧНАЯ ТАБЛИЦА
2-ная
000
001
010
011
100
101
110
111
8-ная
0
1
2
3
4
5
6
7
Известный французский астроном, математик и физик Пьер Симон Лаплас(1749–1827) писал об историческом развитии систем счисления, что «Мысль выражать все числа девятью знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна. Как нелегко было прийти к этому методу, мы видим на примере величайших гениев греческой учености Архимеда и Аполлония, от которых эта мысль осталась скрытой.»
Сравнение десятичной системы исчисления с иными позиционными системами позволило математикам и инженерам-конструкторам раскрыть удивительные возможности современных недесятичных систем счисления, обеспечившие развитие компьютерной техники.
