2.4. Почему люди пользуются десятичной системой, а компьютеры — двоичной?
Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.
А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
для ее реализации нужны технические устройства с двумя устойчивыми состояниями(есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
представление информации посредством только двух состояний надежноипомехоустойчиво;
возможно применение аппарата булевой алгебры
двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
2.5. Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа
в этих системах читаются почти так же
легко, как десятичные, требуют
соответственно в три (восьмеричная) и
в четыре (шестнадцатеричная) раза меньше
разрядов, чем в двоичной системе (ведь
числа 8 и 16 — соответственно, третья и
четвертая степени числа 2).
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Например:
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
Например,
2.6. Как перевести целое число из десятичной системы в любую другую позиционную систему счисления?
Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком («нацело») на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения.
Пример:Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Ответ:7510= 1 001 0112= 1138= 4B16.
2.7. Как пеpевести пpавильную десятичную дpобь в любую другую позиционную систему счисления?
Для
перевода правильной десятичной дpоби
F в систему счисления с основанием
q необходимо F умножить на
q , записанное в той же десятичной системе,
затем дробную часть полученного
произведения снова умножить на q, и
т. д., до тех пор, пока дpобная часть
очередного пpоизведения не станет pавной
нулю, либо не будет достигнута требуемая
точность изображения числа F в
q-ичной системе.
Пример.Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше.
4.4. Почему люди пользуются десятичной системой, а компьютеры — двоичной?
Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.
А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
представление информации посредством только двух состояний надежно и помехоустойчиво;
возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
4.
 5. Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?
5. Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр). |
Например:
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой. |
Например,
4.6. Как перевести целое число из десятичной системы в любую другую позиционную систему счисления?
Для перевода целого
десятичного числа N
в систему счисления с основанием q необходимо N
разделить с остатком («нацело»)
на q , записанное в той
же десятичной системе. |
Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
4.7. Как пеpевести пpавильную десятичную дpобь в любую другую позиционную систему счисления?
Для перевода правильной десятичной дpоби F в систему счисления с основанием q необходимо F умножить на q  |
Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше. |
Почему в компьютере используется двоичная система счисления — что делать, ответы экспертов
Начну издалека. Когда проектировали первые электронные вычислительные машины, то пришли к выводу, что легче всего фиксировать два состояния в электронной схеме. Допустим — есть ток, или его нету. Фиксировать больше 2-х состояний, например, три: нет тока, есть слабый ток, есть сильный ток — не совсем надёжно, ибо изредка при помехах отличить слабый ток от сильного тока трудно. А уж различать десять состояний — это фактически невозможно. Поэтому вся элементарная база строилась на ‘триггерах’, фиксирующих два состояния — ‘включено’, ‘выключено’. Соответственно для этой элементарной базы обычная десятичная система счисления была бы громоздкой, идеально подошла двоичная система, имеющая всего два числа 0 и 1. Под эту систему счисления стали готовить все процессоры. Машина прекрасно понимала эту систему, а вот человеку, программисту, пользоваться ею не совсем удобно, ибо числа имеют много разрядов для своей записи. Например, десятичное число 1234 в двоичной системе записывалось бы как 10011010010. Поэтому программисты для себя стали использовать восьмеричную систему счисления, в ней это же число выглядело так 2322, а то и шестнадцатеричную систему, там уже это число выглядит так 4D2. По какой причине именно 8-ми и 16-тиричные системы? Эти числа, 8 и 16 степени числа 2, потому переводить числа из из нотации в двоичную систему легче, чем из нашей привычной, десятичной. И так, вот первые числа от 0 до 9, записанные в двоичной системе: 0, 1, десять, 11, сто, 101, 110, 111, 1000, 1001. Как видно, двоичная число десять станет равно двойке в десятичной системе. Это про два типа людей. немного поправлю.
Как видно, двоичная число десять станет равно двойке в десятичной системе. Это про два типа людей. немного поправлю.
»двоичная система, имеющая всего два числа 0 и 1″ две цифры же.
» для себя стали использовать восьмеричную систему счисления» потому что компьютерное «слово», кусок данных который проц мог обрабатывать за 1 такт, было длиной 8 бит или байт.
Когда появились 16-битовые слова, то программисты перешли на 16-ричную систему. — 2 месяца назад С поправкой про цифру — согласен, тут у меня конечно же, описка.
А вот с остальным — нет, не согласен. Никак эти системы счисления напрямую с длиной машинного слова не были связаны. Ничего не мешает описывать 8-ми разрядные слова 16-тиричной системой и наоборот. Восьмеричная система и до ныне имеет место быть, хоть уже и не так часто, а вот 32-хричную не используют, хотя уже машинные слова давно перевалили за 16 разрядов. — 2 месяца назад «32-хричную, вернее 33-ную, используют для кодирования русских слов при письме.
:) — 2 месяца назад А знаки препинания? — 2 месяца назад а знаки действия с числами? — 2 месяца назад Вот именно. — 2 месяца назад
Почему люди пользуются десятичной системой а компьютеры — двоичной?, стр.2
Почему люди пользуются десятичной системой, а компьютеры — двоичной?
Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.
А компьютеры используют двоичную систему потому, что она имеет ряд
для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
представление информации посредством только двух состояний надежно и помехоустойчиво;
возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).
Перевод чисел из одной системы счисления в другую
Количество p различных цифр, употребляемых в позиционной системе определяет название системы счисления и называется основанием системы счисления – «p«. Любое число N в позиционной системе счисления с основанием p может быть представлено в виде полинома от основания p:
N = anpn+an-1pn-1+ … +a1p+a0+a-1p-1+a-2p-2+ … (1.1)
здесь N – число, aj – коэффициенты (цифры числа), p – основание системы счисления (p>1). Принято представлять числа в виде
последовательности цифр:
Принято представлять числа в виде
последовательности цифр:
N = anan-1 … a1a0 . a-1a-2 …
Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы (см. формулу 1.1), из которой число переводится. Затем подсчитывается значение суммы.
Перевод целых десятичных чисел в недесятичную систему счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.
Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
Перевод правильных дробей из десятичной системы счисления в недесятичную. Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.
Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Для перевода неправильной
десятичной дроби в систему счисления
с недесятичным основанием необходимо отдельно перевести целую
часть и отдельно дробную. Перевести
23.125102
с.с.
Перевести
23.125102
с.с.
1. Переведем целую часть: | 2. Переведем дробную часть: | 3. Таким образом: |
2310 = 101112; 0.12510 = 0.0012. Результат: 23.12510 = 10111.0012. |
Системы счисления называются кратными, если выполняется соотношение: S = RN, где S, R – основания систем счисления, N – степень кратности (целое число: 2, 3 … ).
Для перевода числа из системы счисления R в кратную ей систему счисления S поступают следующим образом: двигаясь от точки влево и вправо, разбивают число на группы по N разрядов, дополняя при необходимости нулями крайние левую и правую группы. Затем группу заменяют соответствующей цифрой из системы счисления S.
Таблица
Перевести 1101111001.11012«8» с.с. | Перевести 11111111011.1001112«16» с.c. |
Для перевода числа из системы
счисления S в кратную ей систему счисления R достаточно заменить каждую
цифру этого числа соответствующим
числом из системы счисления R,
при этом отбрасывают незначащие нули
в старших (00512)
и младших (15,124000)
разрядах.
Перевести 305.48«2» с.с. | Перевести 7B2.E16«2» с.с. |
Если требуется выполнить перевод из системы счисления S в R, при условии что они не являются кратными, тогда нужно попробовать подобрать систему счисления K, такую что: S = KN и R = KN.
Перевести 175.248«16» с.с.
Результат: 175.248 = 7D.516.
Если систему счисления K подобрать не удается, тогда следует выполнить перевод используя в качестве промежуточной десятичную систему счисления.
Для всего этого примеры
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Например:
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой. Например:
Сложение в различных системах счисления
Таблицы сложения легко составить, используя Правило Счета.
Вычитание в различных системах счисления
Умножение в различных системах счисления
Выполняя умножение многозначных
чисел в различных позиционных системах
счисления, можно использовать обычный
алгоритм перемножения чисел в столбик,
но при этом результаты перемножения и
сложения однозначных чисел необходимо
заимствовать из соответствующих
рассматриваемой системе таблиц умножения
и сложения.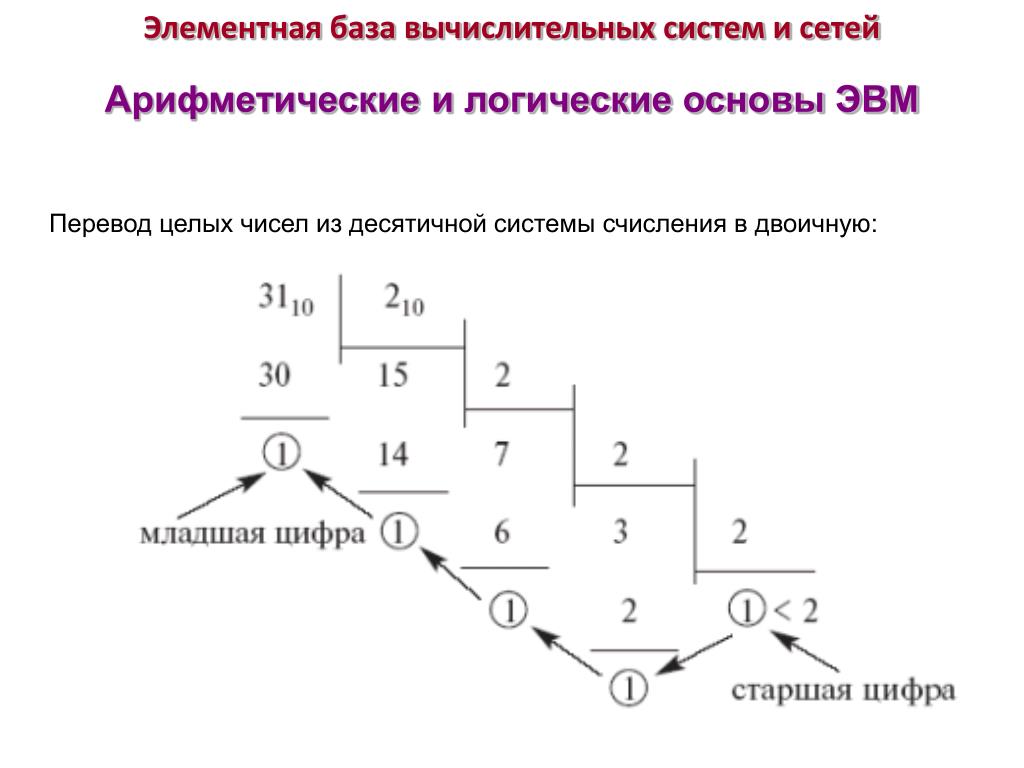
Деление в различных системах счисления
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.
Вопреки распространённому заблуждению, двоичная система счисления была придумана не инженерами-конструкторами ЭВМ, а математиками и философами задолго до появления компьютеров, ещё в 17 веке. Великий немецкий учёный Лейбниц считал: |
Урок «Системы счисления — информатика, уроки
Фирсова Наталия Анатольевна, г. Серов, МБОУ СОШ № 27
«Мысль выражать все числа десятью знаками, придавая им кроме значения по форме еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна»
П. Лаплас
Урок по теме «Системы счисления»
Учитель (постановка проблемы): «Загадочная автобиография». В бумагах одного чудака информатика найдена бала его автобиография. Она начиналась следующими удивительными словами:
«Я окончил курс университета 44 (25 лет) лет от роду. Спустя год, 100-летним (26-летним) молодым человеком, я женился на 34-летней (20-летней) девушке. Незначительная разница в возрасте – всего 11 лет (6 лет) – способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет у меня бала уже и маленькая семья из 10 детей (5 детей), и т.д.»
Учитель: Чем объяснить странные противоречия в числах этого отрывка? (принимаются разные ответы учащихся)
Учитель: Ответить на этот вопрос мы сможем, изучив тему: «Системы счисления».
Цель урока: изучить системы счисления, использующиеся для записи чисел в компьютере, научиться переводить десятичные числа в разные системы счисления.
Учитель: Современный человек в повседневной жизни постоянно сталкивается с числами и цифрами — они с нами везде. А две тысячи лет назад, что знал человек о числах? А пять тысяч лет назад? Ученые утверждают, что и тогда люди могли записывать числа и выполнять над ними арифметические действия, но делали они это совершенно по другим принципам, чем это делаем это мы.
А две тысячи лет назад, что знал человек о числах? А пять тысяч лет назад? Ученые утверждают, что и тогда люди могли записывать числа и выполнять над ними арифметические действия, но делали они это совершенно по другим принципам, чем это делаем это мы.
Система счисления — способ записи (изображения) чисел.
Система счисления — это знаковая система, в котором числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
Учитель: Сейчас мы узнаем о системах счисления, возникших в глубокой древности, ныне исчезнувших, но заложивших основы современных систем счисления. (ПРЕЗЕНТАЦИЯ учащегося)
Учитель: Системы счисления бывают: позиционными и непозиционными.
Непозиционные:
- Единичная система счисления
- Древнеегипетская непозиционная система счисления
- Римская система счисления
- Алфавитные системы счисления
Позиционные:
- Десятичная система счисления
- Двоичная система счисления
- Восьмеричная система счисления
- Шестнадцатеричная система счисления
В информатике и вычислительной технике часто используются основания 2 (двоичная система счисления), 8 (восьмеричная система счисления) и 16 (шестнадцатеричная система счисления). Двоичная система счисления связана с особенностями функционирования цифровых электронных схем, работающих с двумя состояниями, выражаемыми цифрами 0 и 1.
Человек использует десятичную систему счисления, а компьютер – двоичную систему счисления. Поэтому часто возникает необходимость перевода чисел из одной системы счисления в другую.
Научимся переводить из 10-тичной СС в двоичную, восьмеричную, шестнадцатеричную СС. Обратимся к демонстрации: http://files.school-collection.edu.ru/dlrstore/78ba290c-0f7c-4067-aaf4-d72f40f49f3b/9_109.swf (смайлик на слайде).
Для перевода чисел из 10-ой СС в 2-ную, 8-ную и 16-ную СС можно воспользоваться на начальном этапе алгоритмом, который у вас есть на партах:
Алгоритм перевода чисел из десятичной системы счисления в любую другую
- Разделить данное число на основание новой системы счисления. Зафиксировать целое частное и остаток от деления (остаток всегда меньше основания).
- Если полученное частное больше основания, то разделить частное на основание и вновь зафиксировать новое частное и остаток от деления.
- Повторять процесс до тех пор, пока частное не получится меньше делителя.
- Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с ее алфавитом.
- Записать последнее частное и полученные остатки в обратном порядке в ряд слева направо.
Учимся переводить из 10-тичной в 2, 8, 16-ричную СС по принципу «Делай как я…». Учитель показывает перевод столбиком двух разных чисел, а затем учащиеся по рядам закрепляют действия перевода.
Оценочный этап урока: Данный вопрос входит в экзаменационные материалы как ГИА-9, так и ЕГЭ. Поэтому: Тихо! Идет экзамен! (тестирование на ПК с использованием программы «MyTest» или раздаточные карточки с заданиями).
Поэтому: Тихо! Идет экзамен! (тестирование на ПК с использованием программы «MyTest» или раздаточные карточки с заданиями).
Примеры тестовых заданий
- Как представлено число 3510 в двоичной системе счисления?
|
1) 1100012 |
2) 1000112 |
3) 100112 |
4) 110102 |
Ответ: 2)
- Как представлено число 4610 в двоичной системе счисления?
|
1) 1010012 |
2) 1110012 |
3) 1011102 |
4) 111012 |
Ответ: 3)
- Количество значащих нулей в двоичной записи десятичного числа 126 равно
Ответ: 1).
4. Сколько единиц в двоичной записи числа 195?
Ответ: 4).
Учитель: Проверим (показываются ответы). Кто сдал экзамен, поднимите руки!
Кто сдал экзамен, поднимите руки!
Блиц опрос класса для анализа понимания пройденного материала:
- Что такое система счисления? (Способ записи (изображения) чисел).
- Какие виды СС Вы знаете? (Позиционные и не позиционные).
- С какими позиционными СС мы познакомились ранее?
- Какие символы использованы в них для записи чисел? (Арабские цифры, буквы английского алфавита …).
- (На внимательность): В какой системе счисления малыш показывает на пальцах, сколько ему лет? Ответ: в палочной (пальцевой) не позиционной СС — значение числа — количество пальцев — подсчитывается простым суммированием.
Учитель: Вернемся к началу урока (автобиография). И попробуем вновь ответить на поставленный вопрос: Чем объяснить странные противоречия в числах этого отрывка? (ответы учащихся). Учитель открывает решение данной задачи.
Домашнее задание. Пересказ параграфа 16. Составить свою автобиографию в 4-ной системе счисления.
Это нам предстоит сделать на практическом занятии:
|
Ей было 1100 лет. Она в 101 класс ходила. В портфеле по 100 книг носила. Все это правда, а не бред. Когда пыля десятком ног, Она шагала по дороге, За ней всегда бежал щенок С одним хвостом, зато стоногий, Она ловила каждый звук Своими десятью ушами, И 10 загорелых рук
Портфель и поводок держали. И 10 темно-серых глаз Оглядывали мир привычно. Но станет все совсем обычным, Когда поймете наш рассказ. |
СИСТЕМЫ СЧИСЛЕНИЯ | Наука и жизнь
В повседневной жизни мы, как правило, пользуемся десятичной системой счисления. Но это лишь одна из многих систем, которая получила свое распространение, вероятно, по той причине, что у человека на руках 10 пальцев. Однако эта система не всегда удобна. Так, в вычислительной технике применяется двоичная система счисления.
Так, в вычислительной технике применяется двоичная система счисления.
Системой счисления называют совокупность приемов и правил наименования и обозначения чисел, с помощью которых можно установить взаимно однозначное соответствие между любым числом и его представлением в виде совокупности конечного числа символов.
В разные исторические периоды развития человечества для подсчетов и вычислений использовались те или иные системы счисления. Например, довольно широко была распространена двенадцатеричная система. Многие предметы (ножи, вилки, тарелки, носовые платки и т. д.) и сейчас считают дюжинами. Число месяцев в году двенадцать. Двенадцатеричная система счисления сохранилась в английской системе мер (например, 1 фут = 12 дюймам) и в денежной системе (1 шиллинг = 12 пенсам).
В древнем Вавилоне существовала весьма сложная шестидесятеричная система. Она, как и двенадцатеричная система, в какой-то степени сохранилась и до наших дней (например, в системе измерения времени: 1 час = 60 минутам, 1 минута = 60 секундам, аналогично в системе измерения углов: 1 градус = 60 минутам, 1 минута = 60 секундам).
У некоторых африканских племен была распространена пятеричная система счисления, у ацтеков и народов майя, населявших в течение многих столетий обширные области американского континента, — двадцатеричная система. У некоторых племен Австралии и Полинезии встречалась двоичная система.
Десятичная система возникла в Индии. Впоследствии ее стали называть арабской потому, что она была перенесена в Европу арабами. Цифры, которыми мы теперь пользуемся, — арабские.
В разное время существовали и другие записи цифр, в настоящее время почти забытые. Однако до сих пор мы иногда встречаемся с записью чисел с помощью букв латинского алфавита, например на циферблатах часов, в книгах для обозначения глав или частей, на деловых бумагах для обозначения месяцев и т.д.
В вычислительной технике применяется двоичная система счисления. Основанием этой системы является число 2. Это означает, что для представления любого числа используются только две цифры, 0 и 1. Целесообраз ность применения двоичной системы в цифровой электронике объясняется тем, что базовый элемент любой электронной схемы имеет два состояния, которым можно приписать значения 0 и 1.
Это означает, что для представления любого числа используются только две цифры, 0 и 1. Целесообраз ность применения двоичной системы в цифровой электронике объясняется тем, что базовый элемент любой электронной схемы имеет два состояния, которым можно приписать значения 0 и 1.
Рассмотрим для примера двоичное число 110010. Единицы и нули в двоичном числе называют разрядами (битами), а положение каждого бита определяет величину показателя степени основания 2, причем старший значащий разряд находится в числе слева, как и в десятичной системе, а младший — справа. Таким образом двоичное число 110010 в десятичной системе равно 1x25+1x24 +0x23+0x22 +1x21+0x20 = 50. Обратное преобразование целого числа производится методом последовательного деления на 2 до тех пор, пока частное от деления не станет равным 1. Число в двоичной системе счисления записывается в виде остатков от деления, начиная с последнего частного, справа налево.
Почему компьютеры используют двоичные числа | Конвертировать в двоичный онлайн
Строки нулей и единиц. Двоичные числа часто используются для работы с компьютерами. Но почему так? Почему компьютеры конвертируют в двоичный код и из него, а не просто используют основание 10? Здесь мы предоставим вам все ответы, чтобы вы точно знали, почему компьютеры используют двоичные числа!
Современные компьютеры для работы используют двоичные числа — это факт, хорошо известный людям, изучающим информатику, или тем, кто использует эти машины более чем часто.Когда бит произносится, человек, использующий его, пытается определить сокращение двоичной цифры — элемент, который может содержать только 0 или 1. Биты организованы в восемь групп, и эти группы называются октетами или байтами. Обычно октеты имеют размер 23 или 64 бита, поэтому их можно объединить в слова. И это то, о чем знает большинство людей. То, о чем большинство людей не знает, — это причина этого.
Почему компьютеры используют двоичные числа? Вопрос кажется достаточно простым, но ответ на него не такой однозначный.В конце концов, чтобы получить соответствующий ответ, мы сначала должны понять и объяснить, почему инженеры и ученые, проектирующие современные компьютеры, не используют десятичную систему счисления, которой нас учили в школе, и почему используют совершенно незнакомую систему счисления для компьютеры и другие подобные машины.
Хорошая новость заключается в том, что причины, по которым инженеры и ученые используют двоичную систему счисления для компьютеров, легко понять. В конце концов, вы можете легко взять текст сегодня и преобразовать его в двоичный файл онлайн.Итак, не теряя времени, давайте разберемся, почему компьютеры используют двоичные числа, а не другие системы счисления.
Что такое двоичный код и как он работаетПрежде чем мы перейдем к вопросу о том, почему компьютеры используют двоичные числа и конвертируют их в двоичные онлайн, давайте кратко рассмотрим, что такое двоичные числа и как они работают. Используемая компьютерами и некоторыми другими электронными устройствами, двоичная система основана на двух символах: 0 и 1. Таким образом, вы считаете только 0 и 1, и нет никакого символа для двоих, и он представлен десятью.Точно так же, как в десятичной системе счисления есть единицы, тенденции, сотни и тысячи, двоичная система счисления содержит единицы, четверки, восьмерки, шестнадцать и так далее.
В двоичной системе счисления нули и единицы представлены как ВЫКЛ и ВКЛ соответственно. Это указывает на включение или выключение электрического сигнала или экспоненты с основанием 2. Возможно, это вас немного сбивает с толку, но хорошая новость заключается в том, что здесь подробно объясняется эта концепция. Разобравшись с этим, давайте перейдем к вопросу, почему компьютеры используют двоичные числа.
Почему компьютеры используют двоичные числа? Наконец мы подошли к вопросу на миллион долларов: почему компьютеры используют двоичные числа? Ответ не так однозначен, как вы могли подумать. Тем не менее, мы постараемся сделать все возможное, чтобы дать ответы, которые звучали бы логично и поддерживали использование компьютеров в двоичных числах.
Тем не менее, мы постараемся сделать все возможное, чтобы дать ответы, которые звучали бы логично и поддерживали использование компьютеров в двоичных числах.
Чтобы представить числовые данные в нашей повседневной жизни, мы используем десятичную систему счисления. К сожалению, компьютеры не могут. Вместо этого компьютеры представляют числа, используя самую низкую используемую нами систему счисления — два.Это двоичная система счисления. В компьютерах используются напряжения, и, поскольку напряжения часто меняются, для каждого числа в десятичной системе не установлено конкретное напряжение. По этой причине двоичная система измеряется как система с двумя состояниями, то есть включено или выключено. Кроме того, чтобы упростить вычисления и преобразовать их в двоичную систему онлайн, компьютеры используют двоичную систему счисления.
Более сотни правил были бы подключены к компьютеру, если бы мы использовали десятичную систему счисления для компьютеров. Но благодаря двоичной системе вычислений компьютерам требуется только четыре правила.И последнее, но не менее важное: основная причина, по которой компьютеры используют двоичную систему, заключается в том, что система с двумя состояниями является системой счисления, которая лучше всего подходит для оптических и магнитных компонентов памяти компьютера. Продолжая рассуждать, мы собираемся обсудить возможности хранения двоичной системы.
Какая система использует больше памяти: двоичную или десятичную? Если вы быстро взглянете на обе, вы сразу поймете, что двоичная система занимает больше места, чем десятичная.Но это не удивляет нас ни на один бит, учитывая, что двоичное представление состоит из восьми цифр, а десятичное представление — всего из трех цифр. Но поскольку все они хранятся в двоичном формате, это предположение становится практически неверным. Причина, по которой многие люди считают, что двоичная система занимает больше места, чем десятичная, заключается в том, как первая записывается на экране компьютера.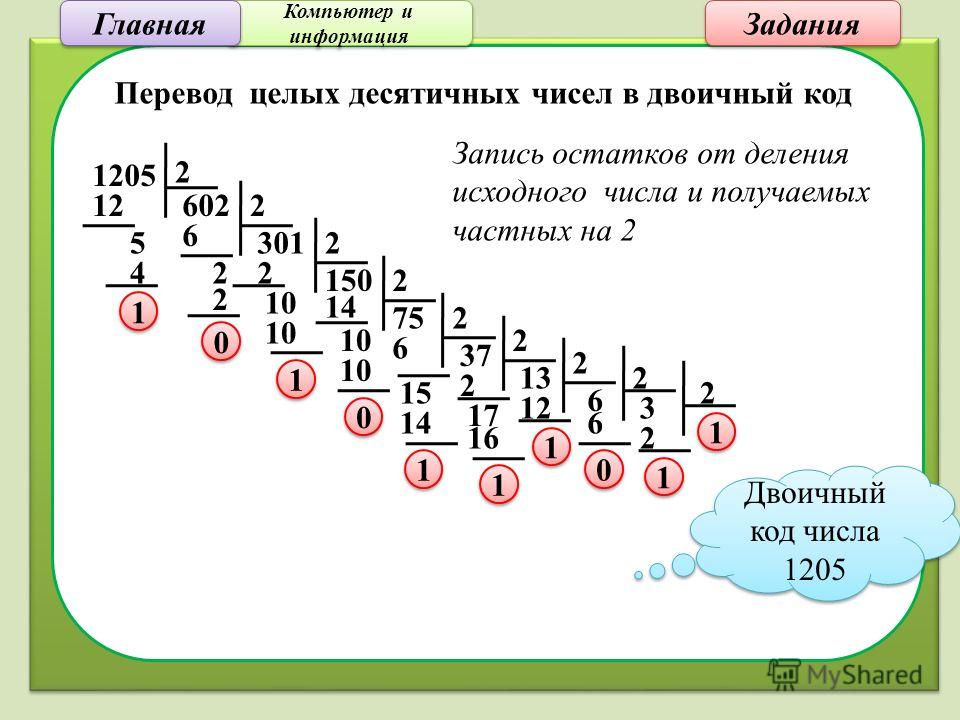
Вы всегда можете уменьшить количество цифр, используемых для представления числа, увеличивая основание, но просто невозможно создать цифровую схему, которая использует что-либо, кроме двух, в качестве основы для работы.Причина в том, что до тех пор, пока вы не переключитесь на квантовые вычисления, между «включено» и «выключено» не будет никакого состояния. Итак, готовы конвертировать в двоичный файл онлайн?
Использование двоичных чисел в цифровых компьютерах и электронных устройствахС помощью переключателей можно кодировать числа в двоичный формат. Эта система может использоваться несколькими цифровыми устройствами, включая часы, декодер цифрового ТВ, калькулятор, охранную сигнализацию, сотовый телефон и компьютер. В памяти значения хранятся в двоичном формате.По сути, это набор электронных переключателей ВКЛ и ВЫКЛ. Предположим, вам доступен набор из восьми кулисных переключателей, и в зависимости от того, включен он или выключен, каждый переключатель может представлять 0 или 1.
Теперь, чтобы сохранить двоичное значение числа, придумайте число и установите переключатели в положение «включено» или «выключено». Кто-то другой мог бы прочитать номер, если бы посмотрел на переключатели. Транзисторы используются в компьютерах для реализации переключателей. Знаете ли вы, какая конфигурационная память самая маленькая? Это единственный бит — то, о чем мы говорили ранее.Для реализации этой памяти конфигурации требуется только один переключатель. При объединении восьми переключателей получается байт. Преобразуйте в двоичный файл онлайн, чтобы лучше понять это.
Переключатели могут быть включены и выключены с помощью цифрового оборудования. Кроме того, оборудование может считывать состояние переключателей. если имеется восемь переключателей, то умножение этого на два по основанию даст использование более 250 компоновок или перестановок в зависимости от состояния переключателя, то есть от того, включен он или выключен.
Вы получили ответ на свой вопрос, т.е. поняли, почему компьютеры используют двоичные числа? Если нет, то мы подведем итоги таким образом, чтобы вам было легче понять, почему компьютеры используют двоичную систему и конвертируют ее в двоичную в режиме онлайн.
В школе нас всех учат использовать десятичную систему счисления, и поэтому она становится стандартной системой счисления, которую мы используем в нашей повседневной жизни.Итак, почему компьютеры не используют эту систему, а вместо этого используют двоичный код? Ответ на этот вопрос довольно прост. Переключатели, управляющие электрическими сигналами, — это то, что электрическая схема мотора выполняет, а «включено» и «выключено» — единственные два состояния, требуемые для этих переключателей. Это означает, что переключатели требуют только два числа: 0 и 1 для представления каждого состояния.
С другой стороны, если бы компьютеры использовали десятичную систему, у переключателя было бы десять возможных состояний. Это отнимает много времени и совершенно не нужно.Итак, чтобы избежать хлопот и упростить вычисления, компьютеры используют двоичную систему счисления. Теперь вы понимаете, почему компьютеры используют двоичные числа вместо десятичных?
Начать преобразование текста в двоичныйТеперь, когда вы знаете, почему компьютеры используют двоичные числа, пора приступить к преобразованию текста в двоичные. Чтобы избежать проблем с использованием физического инструмента, конвертируйте в двоичный файл онлайн. Все символы хранятся в компьютерах как числа двоичных данных.Цифры: 0 и 1 используются двоичным кодом для представления компьютерного текста или инструкций, а каждому символу или инструкции присваивается битовая строка. Назначенные строки могут соответствовать символам, буквам или инструкциям. Кодирование данных — это то, для чего эти коды используются в вычислениях.
С помощью онлайн-инструмента двоичного преобразования вы можете преобразовывать файлы в двоичные файлы и обратно. Вы также можете преобразовать систему base-10, обычно используемую нами с помощью этого инструмента. Кроме того, если вам требуется четыре двоичных цифры для представления одной шестнадцатеричной цифры, вы можете использовать этот инструмент для преобразования в двоичное и шестнадцатеричное и обратно.
Вы также можете преобразовать систему base-10, обычно используемую нами с помощью этого инструмента. Кроме того, если вам требуется четыре двоичных цифры для представления одной шестнадцатеричной цифры, вы можете использовать этот инструмент для преобразования в двоичное и шестнадцатеричное и обратно.
Почему компьютеры используют двоичные числа [Ответил]?
Все мы знаем, что такое десятичные числа: 1, 2, 3, 4, 5 и т. Д. Однако существует много других систем счисления, и вы, возможно, слышали или видели другие, например, шестнадцатеричные числа (например: 3F2B ) или
. двоичные числа (например: 10101011 ), которые могут показаться загадочными и бессмысленными.
Эти шестнадцатеричные или двоичные числа можно легко преобразовать в хорошо известные десятичные числа. Итак, почему существуют эти другие системы и зачем они нам нужны, несмотря на «нормальные» десятичные числа (1, 0, 9, 2 и т. Д.))
можно использовать для всего, что только можно придумать?
Существуют и другие системы счисления, потому что в некоторых случаях использование одной системы счисления проще и дает преимущества перед другой.
- Наша наиболее распространенная система счисления — десятичная (или десятичная). В нем 10 цифр (0–9), которые можно использовать для описания любого возможного числа, которое мы используем ежедневно. Он очень удобен для подсчета и расчетов,
плюс самый интуитивно понятный. - Другая система счисления — шестнадцатеричная (или «основание 16»). Он имеет 16 цифр (0-9 и A-F). Очень удобно описывать значение байтов, используемых в информатике.
- Третья система счисления — это двоичная (или «основание 2») система. Он имеет 2 цифры
(0 и 1), и он используется для представления значения битов — типа информации, хранящейся в памяти компьютера. Он имеет различные преимущества в электронике, а также предлагает определенные математические преимущества.
Двоичные и шестнадцатеричные числа широко используются в информатике. В этой статье мы сосредоточимся на двоичных числах. Двоичные числа можно рассматривать как самое базовое представление числа в электронном устройстве.
Они представляют состояние ВКЛ (1) и состояние ВЫКЛ (0). Многие из этих состояний ВКЛ и ВЫКЛ представляют собой десятичные числа, например:
| Двоичный | Десятичное |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 1000 | 8 |
Преобразование в десятичное и обратно будет рассмотрено в другой статье.А пока мы ответим, почему компьютеры используют двоичную («основание 2») систему счисления и почему электронные устройства хранят двоичные числа.
Это поможет объяснить, почему двоичные числа так важны. Самые первые компьютеры использовали двоичные числа, и они используются до сих пор.
Двоичный код в электронике
Двоичный сигнал: 010101010Каждый компьютер состоит из множества электронных компонентов. Вот почему необходимы базовые знания в области электроники, чтобы понять, как и почему двоичные числа используются в компьютерах.Мы будем делать это очень просто.
Компьютер имеет множество соединений и компонентов, которые используются для передачи и хранения данных, а также для связи с другими компонентами. Большая часть этого хранения, передачи и обмена
происходит с помощью цифровой электроники. Цифровая электроника использует двоичную систему (ВКЛ / ВЫКЛ). Сигнал с серией импульсов ВКЛ / ВЫКЛ равен двоичному числу.
В электронике уровень напряжения или ток — это способ представления значения. Например, 5В (вольт) или 0.5А (амперы). Конечно, производители электронных устройств могут придавать значение
разным значениям напряжения. Если вам нужно 10 значений, вы можете разделить диапазон 0–4 В (включая 0, что создает 5 «шагов») на 10. В итоге вы получите 0,5 В на шаг:
В итоге вы получите 0,5 В на шаг:
| V | Шаг |
| 0,0 | 1 |
| 0.5 | 2 |
| 1,0 | 3 |
| 1,5 | 4 |
| 2,0 | 5 |
| … | … |
Однако чем выше напряжение или ток, тем выше потребление энергии устройством.
Вы видите здесь проблему?
Ну, чем выше напряжение или ток, тем выше потребление энергии устройством.
Это означает, что при создании электронного устройства чаще всего желательно иметь как можно более низкое потребление энергии и низкое напряжение.Кроме того, электронные сигналы не всегда стабильны (
) и могут изменяться из-за окружающих воздействий, таких как близлежащие внутренние схемы других электронных устройств.
Используя 0,5 В на шаг из предыдущего примера, мы предполагаем, что электронные схемы могут влиять на уровни напряжения и заставлять их казаться на 0,25 В выше или ниже (это произвольный пример).
Это может затем привести к уровням напряжения, при которых будет трудно различить, какое значение оно представляет. Напряжение 0.5 может означать 1, 2 или 3, поскольку существует вероятность того, что он попадет в диапазон от 0,25 В до 0,75 В.
| В | Мин. | Макс. | Шаг |
| 0,0 | -0,25 | 0,25 | 1 |
| 0,5 | 0,25 | 0.75 | 2 |
| 1,0 | 0,75 | 1,25 | 3 |
| 1,5 | 1,25 | 1,75 | 4 |
| … | … | … | … |
В результате мы не можем разделить 5 В на 10 ступеней. Ценности могут быть неверно истолкованы. Компьютер может внезапно сделать неправильные вычисления из-за случайных помех.
Ценности могут быть неверно истолкованы. Компьютер может внезапно сделать неправильные вычисления из-за случайных помех.
Этот пример диапазонов напряжения показывает, что необходимо иметь безопасный диапазон между двумя уровнями напряжения, чтобы считывать правильное значение со 100-процентной вероятностью.(На уровне программного обеспечения
есть дополнительные методы для проверки правильности считывания данных, но это выходит за рамки данной статьи). Это одна из причин, почему в компьютерах используется двоичная система, использующая только два уровня / состояния. Двоичный код происходит от латинского языка
и означает, что что-то состоит из двух частей. Двоичную электронику обычно называют цифровой электроникой.
Другая важная причина заключается в том, что требуется гораздо больше схем, чтобы различать более двух уровней напряжения.Каждое дополнительное состояние требует примерно такого же количества дополнительных схем. Например, для двоичной системы требуется
2 * n (n = размер схемы). Для системы с тремя состояниями необходимо 3 * n. И так далее.
Компьютеры используют двоичную систему по двум причинам.
- Два четко разных состояния обеспечивают безопасный диапазон надежности.
- Наименьшее количество необходимых схем, что приводит к наименьшему количеству места, потреблению энергии и стоимости.
Однако квантовые вычисления однажды могут заменить двоичную систему.Это может стать следующим большим шагом в понимании того, как работают наши компьютеры!
Почему компьютеры используют двоичный код
Двоичный — это латинское слово, означающее «состоящий из двух». Двоичная система счисления содержит только эти две цифры: 0 и 1.
Система двоичного кодирования стандартизирована для совместимости с различными платформами. Если бы у вас был компьютер под управлением Windows с двоичной системой, а у вашего друга компьютер Mac с десятичными числами, общение было бы действительно затруднительным.
Компьютеры постоянно переводят все, что вы видите на экране компьютера и смартфона, в двоичную систему счисления . Это потому, что они не понимают используемую нами десятичную систему счисления (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
Помимо двоичной системы, в компьютерной науке также широко используется шестнадцатеричная система (основание 16). Компьютеры не работают в шестнадцатеричной системе, но программисты используют ее для представления данных в удобочитаемом формате.Шестнадцатеричная система имеет 16 возможных значений. Он использует 10 десятичных цифр от 0 до 9 и 6 букв алфавита от A до F. Преобразуйте шестнадцатеричный код в двоичный, чтобы увидеть, как закодированы языки программирования.
Когда дело доходит до двоичной системы, у всех нас возникает один и тот же вопрос: если технологии настолько развиты, почему компьютеры все еще используют двоичную систему? Почему они не могут научиться общаться, используя десятичную систему счисления , и английские слова?
Давайте погрузимся в это.
Почему компьютеры используют двоичные числа?
Мы используем наши компьютеры и цифровые устройства каждый день.Но знаете ли вы, что за кулисами ваш смартфон преобразует все в цепочки нулей и единиц взад и вперед, чтобы он мог понять вас, а вы — это? Когда дело доходит до основ, компьютер — это просто центральный процессор, работающий от электрического тока, и обширный набор инструкций.
Цифровые компьютеры были великим изобретением, но у них есть ограничения. Они понимают только двоичные цифры 0 и 1. Они не понимают десятичные цифры и английские слова (код ASCII ), как люди, но они довольно хорошо стараются! Существует очень конкретная причина, по которой компьютеры и другие электронные устройства используют двоичную систему, и все она заключается в одной концепции: Boolean logic .Но прежде чем мы перейдем к этому, давайте разберемся в истинном значении 0 и 1.
Почему нули и единицы?
Бит — это наименьшая единица данных в компьютере. 0 и 1 — два возможных состояния в бит . Все в компьютере представляет собой набор строк, содержащих нули и единицы. Причина, по которой это работает так хорошо, заключается в том, что 0 означает выключено, а 1 означает .
Если бы мы добавили к биту еще одну цифру, это сделало бы вещи более аналоговыми — нам пришлось бы подумать о средних состояниях между включенным и выключенным, например, «немного включен» и «включен много».Использование 0 и 1 гарантирует, что наши значения будут дискретными .
Эти значения 0 и 1 используются для питания электрических сигналов, как мы узнаем в рамках булевой логики.
Понимание логики
Логикабыла разработана парнем по имени Джордж Буль в 1847 году. Возможно, вы уже слышали о логике или алгебре , особенно если вы изучаете информатику. Логическая логика — это основная причина, по которой цифровые компьютеры используют двоичную систему для всего, что они делают.
Логическая математика и двоичная система легко сопоставляются друг с другом. Это связано с тем, что логическая логика также работает по принципу включения и выключения — в логической логике она транслируется как ИСТИНА или ЛОЖЬ .
Логическая логика работает непосредственно с электронными схемами компьютера. Состояние ИСТИНА позволяет электрическому сигналу проходить, а состояние ЛОЖЬ препятствует прохождению электрического сигнала через цифровую схему.
Логическая математикаобрабатывается с помощью этих трех операторов (также называемых логическими вентилями ): ИЛИ, И и НЕ.
ИЛИ — это логический оператор, который возвращает ИСТИНА, если одно или другое или оба выражения истинны. Если какое-либо выражение истинно, ИЛИ возвращает Истинно. Если ни одно из выражений не имеет значения True, OR возвращает False.
AND — логический оператор, который возвращает FALSE, если одно из выражений имеет значение FALSE. И возвращает ИСТИНА, если оба выражения ИСТИНА. Оператор И возвращает ИСТИНА, если оба выражения ЛОЖЬ.
NOT — логический оператор, который возвращает TRUE для каждого выражения FALSE и FALSE для каждого выражения TRUE.
Таблица логической истины
Это удобная таблица, когда вам нужно понять, как логические операторы работают вместе. Рассмотрим два входа A и B, на которые действует оператор.
| A | B | A AND B | A OR B | НЕ А | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ИСТИНА | ИСТИНА | ЛОЖЬ | ИСТИНА | ИСТИНА | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ИСТИНА | ЛОЖЬ | ЛОЖЬ | ИСТИНА | ЛОЖЬ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ИСТИНА | ИСТИНА | ИСТИНА | ИСТИННО система счисления так хорошо работает в компьютерах Двоичная система существует с момента изобретения компьютеров.Он так долго оставался на рынке, потому что отлично справляется со своей работой. Итак, почему двоичная система так хорошо работает в наших электронных устройствах? Проще говоря, комбинация Physics и hardware в компьютерной системе хорошо связывает все вместе. Давай копнем глубже. Физика Двоичная система работает так хорошо, потому что каждый компьютер состоит из электронных компонентов . ОборудованиеМожет показаться, что двоичная система занимает много места. Возьмем, к примеру, двоичный перевод буквы «а» — это 01100001. Похоже, это много цифр.Однако двоичная система ограничивает значения только 0 и 1 , и это делает хранение памяти в компьютере намного более эффективным. Раньше компьютеры использовали громоздкие механизмы и огромные помещения для хранения данных и вычислений. Современные компьютеры используют сотни транзисторов размером всего 5 нанометров для хранения двоичного кода. С этой точки зрения двоичные цифры не занимают много места. Таким образом, учитывая все обстоятельства, выбор двоичной системы для компьютеров имеет смысл. Подводя итогиВ этой статье вы глубоко погрузились в работу вашего компьютера. Все, что скрывается за кадром вашего смартфона, расставлено по нулям и единицам. Перейдите к преобразователю текста в двоичный, чтобы преобразовать текст в двоичную систему цифр. Почувствуйте, как все выглядит внутри вашего смартфона. Почему компьютеры используют двоичный кодДвоичные числа, представляемые как строки из нулей и единиц, часто связаны с компьютеры. Но почему это? Почему компьютеры не могут использовать базовую 10 вместо преобразования? в бинарный и из него? Разве не более эффективно использовать более высокую базу, поскольку двоичная (база 2) представление использует больше «пробелов»? Недавно мне задали этот вопрос кто-то, кто хорошо разбирается в компьютерах. Что такое «цифровой»?Современный «цифровой» компьютер, в отличие от старого «аналогового» компьютера, работает на принцип двух возможных состояний чего-либо — «включено» и «выключено». Это прямо соответствует здесь либо присутствует электрический ток, либо указанный электрический ток отсутствует. Состоянию «включено» присваивается значение «1», а состоянию «выключено» — значение «0». Термин «двоичный» подразумевает «два». Таким образом, двоичная система счисления — это система чисел, основанная на на две возможные цифры — 0 и 1. Здесь на помощь приходят строки двоичных цифр. Каждая двоичная цифра, или «бит», представляет собой отдельную 0 или 1, что напрямую соответствует одному «переключателю» в цепи. Добавьте достаточно этих «переключатели» вместе, и вы можете представить больше чисел. Таким образом, вместо 1 цифры вы получите с 8, чтобы сделать байт. (Байт, основная единица памяти, просто определяется как 8 бит; общеизвестные килобайты, мегабайты и гигабайты являются производными от байта, каждый из которых равен 1024 раз больше, чем другие.Разница в 1024 раза больше, чем в 1000 раз. потому что 1024 — это степень двойки, а 1000 — нет.) Использует ли двоичный код больше памяти, чем десятичный? На первый взгляд это похоже на двоичное представление числа Увеличение базы уменьшит количество цифр, необходимых для представления любого данного числа,
но, исходя непосредственно из предыдущего пункта, невозможно создать цифровую схему, которая
работает в любой базе, кроме 2, поскольку нет состояния между «включено» и «выключено» (если только вы
займемся квантовыми компьютерами . А как насчет восьмеричного и шестнадцатеричного? Восьмеричный (с основанием 8) и шестнадцатеричный (с основанием 16) просто «ярлык» для представления двоичного кода.
числа, так как обе эти базы являются степенями двойки.3 восьмеричные цифры = 2 шестнадцатеричные цифры = 8 двоичных чисел
цифры = 1 байт. Программисту проще представить 32-битное целое число,
часто используется для 32-битных значений цвета, так как Недвоичные компьютерыПредставьте себе компьютер, основанный на десятичных числах. Тогда у каждого «переключателя» будет 10 возможных состояния.Они могут быть представлены цифрами (известными как «запреты» или «точки», что означает «десятичные цифры»). От 0 до 9. В этой системе числа будут представлены в базе 10. Это невозможно с сегодняшними обычными электронными компонентами, но теоретически это возможно на квантовом уровне. Эта система более эффективна? Предполагая, что «переключатели» стандартного двоичного компьютера занимают такое же количество физического пространства (нанометры), что и у этих переключателей base-10, base-10 компьютер сможет разместить значительно большую вычислительную мощность в том же физическом пространстве.Таким образом, хотя вопрос о том, что двоичная система является «неэффективной», имеет некоторое теоретическое обоснование, но сегодня не используется на практике. Почему тогда все современные компьютеры используют двоичный код?Простой ответ: компьютеры изначально не были предназначены для использования двоичных файлов … скорее, двоичные файлы были Мы решили стать наиболее практичной системой для компьютеров, которые мы разработали. Полный ответ:
Мы используем только двоичный код, потому что в настоящее время у нас нет технологии для создания «переключателей». Системы счисленияСистемы счисления В этом учебном курсе используются расширения HTML 3.0 Введение Система счисления определяет набор значений, используемых для представления количество. Мы говорим о количестве людей, посещающих занятия, количество модулей, взятых на одного студента, а также используйте числа для представляют собой оценки, полученные учащимися на тестах. Количественная оценка значений и предметов по отношению друг к другу является помогает нам понять окружающую среду.Мы делаем это в ранний возраст; выясняя, есть ли у нас еще игрушки, с которыми можно поиграть, еще подарки, еще леденцы и так далее. Изучение систем счисления не ограничивается только компьютерами. Мы применяем числа каждый день, и зная, как работают числа, мы дать нам представление о том, как компьютер манипулирует и хранит числа. Человечество на протяжении веков использовало знаки и символы для представляют собой числа. Ранние формы были прямыми линиями или группами линий, как в фильме Робинзон Крузо , где группа из шести вертикальных линий с диагональной линией поперек представлена одна неделя. Сложно представить большие или очень маленькие числа с помощью
такой графический подход. Уже в 3400 г. до н. Римляне изобрели систему счисления, которая могла представлять все числа от 1 до 1000000 с использованием всего семи символов
Маленькая полоса над символом указывает на то, что номер умножить на 1000. Наиболее распространенной сегодня системой счисления является арабский система. Впервые он был разработан индусами и использовался как еще в 3 веке до нашей эры. Введение символа 0, использовался для обозначения позиционного значения цифр, было очень важный. Таким образом, мы познакомились с концепцией групп единиц, десятков единиц, сотен единиц, тысяч единиц и скоро. В системах счисления часто полезно думать о повторяющихся устанавливает , где набор значений повторяется снова и снова. В десятичной системе счисления имеет набор значений. диапазон от 0 до 9. Этот базовый набор повторяется снова и снова. над, создавая большие числа. Обратите внимание, как повторяется набор значений от 0 до 9, и для каждого повторить, столбец слева увеличивается (с 0 до 1, затем 2). Каждое увеличение значения происходит до значения наибольшего число в наборе (9), на этом этапе следующее значение является наименьшим в наборе (0), и новое значение создается в левый столбец (т. е. следующее значение после 9 — 10). 09, 10 - 19, 20 - 29, 30 - 39 и т. Д. Мы всегда записываем цифру с наибольшим значением на слева от номера База
Значения
Взвешивание
Фактор 200 = ----- 0 * 10 0 = 0 * 1 = 0 ------ 0 * 10 1 = 0 * 10 = 0 ------- 2 * 10 2 = 2 * 100 = 200 ----- 200 (суммируя) ----- Рассмотрим еще один пример десятичного числа 312. 312 = ----- 2 * 10 0 = 2 * 1 = 2 ------ 1 * 10 1 = 1 * 10 = 10 ------- 3 * 10 2 = 3 * 100 = 300 ----- 312 (суммируя) ----- десятичный
Система счисления [База-10] 0 1 2 3 4 5 6 7 8 9 , где 0 имеет наименьшее значение, а девять — наибольшее. значение. Цифра или столбец слева имеет наибольшее значение, в то время как цифра справа имеет наименьшее значение. Если при вычислении высшая цифра (9)
превышено, происходит перенос, который переносится в следующий столбец
(Слева). Пример добавления и превышения диапазона базовой настройки 8 + 4 8 9 +1 10 +2 Примечание 1: 11 +3 12 +4 Примечание 1: при превышении 9 мы возвращаемся к началу набора (0), и перенесите значение 1 в следующий столбец слева. Позиционные значения [единицы, десятки, сотни, тысячи и т. Д.
Колонны] 237 = (2 группы по 100) + (3 группы по 10) + (7 групп по 1) = (100 + 100) + (10 + 10 + 10) + (1 + 1 + 1 + 1 + 1 + 1 + 1) = (200) + (30) + (7) = 237 Каждый столбец, перемещаемый влево, в 10 раз превышает предыдущее значение. двоичный
Система счисления [База-2] , где 0 имеет наименьшее значение, а 1 — наибольшее. значение. Столбцы используются так же, как и в десятичная система, в которой крайний левый столбец используется для представления наибольшего значения. Как мы видели в десятичной системе счисления,
значения в наборе (0 и 1) повторяются как по вертикали, так и по
горизонтальные направления. 0 1 10 Примечание: перейти к наименьшему значению в наборе, перенести влево 11 100 Примечание: перейти к наименьшему значению в наборе, перенести влево 101 110 Примечание: перейти к наименьшему значению в наборе, перенести влево 111 . В компьютере двоичная переменная, способная хранить двоичные данные. значение (0 или 1) называется BIT. В десятичной системе столбцы представляют умножение. 1011 = ---- 1 * 2 0 = 1 ----- 1 * 2 1 = 2 ------ 0 * 2 2 = 0 ------- 1 * 2 3 = 8 ---- 11 (в десятичной системе) Числовые диапазоны в двоичном формате с использованием указанного количества бит количество различных значений = 2 n где n - количество бит например.2 8 = 256 разных значений Правила сложения двоичных файлов
1011 + 101 = 1011 101 1.Начните с самого правого столбца и примените правила. 2. 1 + 1 равно 0 и переносит 1 в следующий столбец слева. 1011 101 ------ 0 и нести 1 что действительно похоже 1011 111 ------ 0 3. Теперь займитесь вторым столбцом. 4. 1 + 1 равно 0, перенесите 1 в следующий столбец слева. 1011 111 ------ 00 и нести 1 что действительно похоже 1011 111 1 ------ 00 5.Теперь сделайте третий столбец 6. 1 + 1 равно 0, перенесите 1 в следующий столбец слева. 1011 111 1 ------ 000 и нести 1 что действительно похоже 1011 111 1 ------ 000 7. Теперь займитесь последней колонкой слева. 8. 1 + 1 равно 0 и переносится 1 слева. Правила двоичного вычитания
Правила двоичного умножения
Примеры задач для двоичного сложения
и вычитание Преобразование
Десятичное в двоичное Метод 1: Разделите число на 2, затем разделите то, что осталось на 2 и так далее, пока ничего не останется (0). Записывать остаток (который равен 0 или 1) на каждом этапе деления. Как только делений больше нет, перечислите оставшиеся значения в обратный порядок. Это двоичный эквивалент. 254/2, что дает 127 с остатком 0 127/2, что дает 63 с остатком 1 63/2 получается 31 с остатком 1 31/2 получается 15 с остатком 1 15/2 получается 7 с остатком 1 7/2 дает 3 с остатком 1 3/2 дает 1 с остатком 1 1/2 дает 0 с остатком 1 таким образом, двоичный эквивалент: 11111110 Другой пример, 132 десятичное число 132/2, что дает 66 с остатком 0 66/2, что дает 33 с остатком 0 33/2, что дает 16 с остатком 1 16/2 - 8 с остатком 0 8/2 - 4 с остатком 0 4/2 дает 2 с остатком 0 2/2 дает 1 с остатком 0 1/2 дает 0 с остатком 1 таким образом, двоичный эквивалент 10000100 Метод 2: Каждый столбец представляет степень двойки, поэтому используйте
это как основа для расчета числа.
Примеры задач для преобразования десятичного числа в двоичное
Преобразование Двоичные числа — это
O кталл
Система счисления [База-8] 0 1 2 3 4 5 6 7 , где 0 имеет наименьшее значение, а семь — наибольшее. значение. Столбцы используются так же, как и в десятичной системе, в этом крайнем левом столбце используется для представления наибольшего значения. Как мы видели в десятичной системе счисления,
значения в наборе (0 и 1) повторяются как по вертикали, так и по
горизонтальные направления. 0-7, 10-17, 20-27, 30-37...... Задача: Преобразовать восьмеричное число 176 в десятичное. Каждый столбец представляет степень 8, 176 = ---- 6 * 8 0 = 6 ----- 7 * 8 1 = 56 ------ 1 * 8 2 = 64 ---- 126 Octal широко использовался в ранних мэйнфреймах. системы. шестнадцатеричный
Система счисления [База-16] 0 1 2 3 4 5 6 7 8 9 А Б В Г Д Е Ф , где 0 имеет наименьшее значение, а F — наибольшее значение. Столбцы используются так же, как и в десятичной системе счисления. система, в которой крайний левый столбец используется для представления наибольшая ценность. Как мы видели в десятичной системе счисления,
значения в наборе (0 и 1) повторяются как по вертикали, так и по
горизонтальные направления. 0 - F, 10 - 1 этаж, 20 - 2 этаж, 30 - 3 этаж...... Шестнадцатеричный формат часто используется для представления значений [чисел и адреса памяти] в компьютерных системах.
Преобразование шестнадцатеричного числа в десятичное Каждый столбец представляет степень 16, 176 = ---- 6 * 16 0 = 6 ----- 7 * 16 1 = 112 ------ 1 * 16 2 = 256 ---- 374 Преобразование двоичного числа в шестнадцатеричное Каждая шестнадцатеричная цифра представляет 4 двоичных бита. Разделить двоичное число на группы по 4 бита, начиная справа.1 0110 = 1 = 6 = 16 в шестнадцатеричной системе счисления Преобразование десятичного числа в шестнадцатеричное Используйте тот же метод, который использовался ранее, чтобы разделить десятичную дробь на двоичный, но разделить на 16. 232/16 = 14 с остатком 8 14/16 = 0 с остатком E (14 в десятичной системе = E) = E8 16 Во избежание путаницы мы часто добавляем суффикс для обозначения основания номера 162 ч ч означает шестнадцатеричный 162 16 16 означает основание 16 162 d d означает десятичное 162 10 10 означает основание 10 162 o o означает восьмеричное 162 8 8 означает основание 8 101 b b означает двоичный 101 2 2 означает основание 2 Примеры задач для шестнадцатеричной системы
Преобразование Представляя положительные и
отрицательные числа в двоичном формате Если число отрицательное, знак будет 1 , а для
положительные числа, знак 0 . Вопрос: Что такое диапазон чисел, доступных при использовании 8 бит. Для 8 бит один бит предназначен для знака, 7 для числа, поэтому диапазон значений равен 2 7 = 127 комбинаций Из-за проблем с сложением и вычитанием отрицательный числа обычно хранятся в формате, отличном от положительного числа. Дополнительная информация о представлении чисел Единицы Дополнение
Дополнение до двоек
Другой способ создания дополнительного числа до 2 — начать
наименьший значащий бит и скопируйте все 0 до
достигается первая 1. В следующей таблице показаны как единицы, так и двойки.
дополнить, используя диапазон 4 бита.
Примечание: Посмотрите, как в случае дополнения до 1 есть два представления для 0 Серый Код Код Грея иногда называют отраженным двоичным кодом , потому что первые восемь значений сравниваются с последними 8 значения, но в обратном порядке.
Код Грея часто используется в механических приложениях, таких как
энкодеры вала. Арифметика по модулю 2 Преобразование серого в двоичное
Пример, преобразование 1101101 кода Грея в двоичный Серый двоичный 1.1101101 2. 1 101101 1 копия вниз MSB 3. 1 1 1101 1 0 1 по модулю 2 1 = 0 4. 11 0 1101 1 0 0 0 по модулю 2 0 = 0 3/4 110 1 101 10 0 1 0 по модулю 2 1 = 1 3/4 1101 1 01100 1 0 1 по модулю 2 1 = 0 3/4 11011 0 1 1001 0 0 0 по модулю 2 0 = 0 3/4 110110 1 10010 0 1 0 по модулю 2 1 = 1 Ответ 1001001 Преобразование двоичного изображения в серый
Пример, преобразование двоичного кода 1001001 в код Грея Бинарный серый 1.1001001 2. 1 001001 1 копировать вниз MSB 3. Превышение 3 Серый код Выходы линейных устройств или угловых энкодеров могут кодироваться более 3 кодов Грея для получения многозначных чисел в двоично-десятичном коде.
Главная | Другие курсы | Обратная связь | Примечания | Тесты © Copyright B Brown / Peter Henry. Почему компьютеры используют двоичные числа?Почему компьютеры используют двоичные числа? Двоичная система — это система счисления, в которой 0 и 1 используются только в качестве языка для отображения кодов и данных. Двоичная система — это главный корень, на котором построены цифровые технологии. Эти двоичные числа можно легко преобразовать в наиболее удобные десятичные числа. В компьютере есть переключатели для отображения данных, и эти переключатели имеют только два состояния — ВКЛ и ВЫКЛ.Преимущество двоичной системы заключается в незначительных вычислениях и меньшем количестве ошибок вычислений. Эта система прекрасно подходит для кодирования цифрового сигнала, так как в ней используются только две цифры, то есть 1 и 0, для формирования различных цифр. Кто-то однажды сказал: «В мире есть 10 типов людей, которые понимают двоичный код, а другие — нет». Прочитав эту статью, вы попадете в группу, которая понимает двоичный код, и вы также получите анекдот. Что еще более важно, эта статья поможет вам лучше понять, как работают современные компьютеры. Что такое бит? Наименьшая единица данных в компьютере — это бит. Слово бит — это сокращение от двоичной цифры. Подобно лампочке, бит может быть в одном из двух состояний: включен или выключен. В вычислениях бит представляет собой одиночный сигнал включения или выключения. Внутри электрической цепи эти значения включения или выключения представлены числами 1 и 0 соответственно. Из этих простых битовых компьютеров выстраивайте большие последовательности единиц и нулей для представления сложных данных и инструкций.Строка из восьми бит называется байтом. Байт — это сокращение от двоичного термина. Поскольку эти сигналы включения или выключения состоят из конечных состояний, мы называем их цифровыми. Напротив, аналоговая система может охватывать практически бесконечный диапазон точек. Визуально мы могли бы представить цифровых сигналов как ступенчатых функций и аналоговых сигналов как непрерывных волн. Итак, теперь, когда мы знаем, что такое биты, давайте узнаем, как такая простая система может хранить такой широкий массив информации. Теперь мы узнаем, как представить практически любое число, используя только единицы и нули. Давайте использовать лампочки для обозначения битов. Предположим, у нас есть массив из четырех лампочек. Когда лампочка горит, мы можем представить это состояние как цифру один. И наоборот, мы можем представить выключенное состояние нулевой цифрой. Предположим, что каждая лампочка представляет степень двойки, когда она включена, крайняя правая лампа представляет собой двойную степень до степени нуля, которая равна единице.Следующая лампочка переходит в два в степени 1, что равно 2. Следующая чаша после этого — два в степени два, то есть четыре, и, наконец, крайний левый бит будет представлять 2 в степени 3, которая равна 8. Когда все четыре лампочки включены, мы можем сложить их значения, чтобы получить число 15, так как 8 плюс 4 плюс 2 плюс 1 равно 15. Когда лампочка включена, мы можем представить, что мы умножаем мощность 2 на 1. Когда свет лампа выключена, мы умножаем эту мощность 2 на 0. Таким образом, если все лампочки выключены, мы получаем 0 умножить на 8 плюс 0 умножить на 4 плюс 0 умножить на 2 плюс 0 умножить на 1. Связь между битами X и их значениямиСуществует взаимосвязь между количеством битов и количеством значений, которые могут быть представлены. Как правило, количество битов X может представлять от 2 до X различных значений. Начнем с одного бита, как мы знаем из нашего определения бита. Один бит может представлять в общей сложности два разных значения 0 или 1. С двумя битами мы можем представить четыре разных значения, а именно от 0 до 3. С 3 битами мы можем представить восемь разных значений, от 0 до 7, а с 4 битами мы можем представить 16 различных значений, от 0 до 15. Почему компьютеры используют двоичные числа?Теперь, когда мы знаем, что такое бит и как его можно использовать для хранения чисел, теперь мы готовы узнать , почему компьютеры используют двоичные числа. Итак, сначала мы должны понять, какие компоненты составляют компьютеры, и, по большому счету, одним из наиболее часто используемых компонентов в компьютере в микроскопическом масштабе является транзистор, который по сути является просто переключателем включения и выключения, и это те устройства, которые используются. по сути делать все расчеты и все такое.Каждый другой цифровой компонент по сути построен из транзисторов и других очень маленьких компонентов, собранных вместе на кристалле. Что делает транзистор, поскольку он включен и выключен, он может пропускать электричество или нет. Таким образом, все расчеты и все должны основываться на переключателях включения и выключения, и лучший способ представления данных для системы, которая работает с переключателями включения и выключения, — двоичный, потому что это либо 1, либо 0, он либо включен, либо выключен. . Таким образом, в регистре памяти вы можете хранить вещи в двоичном формате, а затем он запускается через систему через любые процессы и вещи через эти переключатели, и просто проще использовать двоичный код для этой системы, поскольку вы имеете дело с ними нули, переключатели включения и выключения просто имеют смысл с ними, потому что вы можете представлять нули с выключенным, а единицы с включенным. Теперь есть некоторые другие распространенные системы счисления, которые используются в компьютерах, такие как шестнадцатеричные или любые другие системы счисления выше, чем десятичные, и это в основном потому, что это позволяет вам хранить очень большие числа с ограниченным количеством символов, но это не так. не используются на глубоком аппаратном уровне, они обычно используются на программном уровне верхнего уровня для хранения данных, поэтому в целом все в какой-то момент становится двоичным внутри компьютера. Важность чисел в информатикеВажность чисел в информатикеВ вычислениях данные могут быть описаны как любые символы, которые используются для представления чисел и букв.Формат, в котором хранятся данные, известен как представление данных. Контрольный список | Цифровые данные | Двоичный | Шестнадцатеричный | Текст | Графика | Аудио и видео | Битовые ошибки | Обзор и кредиты | Оцененные задания Компьютер — цифровое устройство. Он хранит информацию в одном из двух состояний с использованием двоичного кода. Мы должны определить, как представить значимую информацию, такую как имя, программная инструкция или изображение, в двоичном формате.Вся информация хранится в компьютере с использованием двоичных чисел. Все мы используем различные компьютеры в течение дня, но что делает устройство компьютером? Не многие люди задумываются о том, что именно делает что-то компьютером.
Как бы вы описали компьютер человеку, который никогда не видел цифровых технологий? Одно из моих любимых шоу на канале Discovery — Alaskan Bush People . Когда шоу впервые дебютировало, семья Браун не была знакома с современными технологиями. Как бы вы охарактеризовали компьютер для человека, который живет в зарослях Аляски? Давайте познакомимся с семьей Браунов, чтобы вы могли лучше понять, кому вы объясняете компьютер.
Задание: вопрос для размышления 3.1Маршрут: Представьте, что вы разговариваете с кем-то, кто никогда не использовал цифровые технологии.Как бы вы описали им компьютер? Напишите краткое (~ 75 слов) описание компьютера. Разместите свое описание прямо в текстовом поле в itsLearning. Не прикрепляйте отдельный документ или ссылку на свой Google Диск и проверьте правописание перед отправкой. Когда мы уезжаем в отпуск, мы следуем дорожной карте, такой как бумажная дорожная карта, полученная на остановке для отдыха, или навигационной системе, такой как Google Maps. Ни навигационная система, ни бумажная карта не являются реальной дорогой, по которой вы путешествуете.Вместо этого эти элементы содержат некоторую информацию о маршруте, необходимом для достижения цели добраться от вашего дома до места вашего отпуска. Как и карта, компьютер фиксирует и представляет информацию в форме, необходимой для компьютерной обработки. Силы, формирующие ваше будущее, — это digital , и вам необходимо их понять. Данные повсюду вокруг нас. Практически все, с чем мы связаны, собирает данные. Светофоры подсчитывают, сколько автомобилей проехало на зеленый, желтый или даже красный свет.Продуктовые магазины отслеживают среднюю сумму, потраченную на транзакцию, сколько товаров приобретается за транзакцию и какие товары приобретаются. Торговый автомат в школе отслеживает, когда совершаются покупки. Это всего лишь несколько примеров данных. Но что означают все эти данные? Представление данных относится к методам, используемым компьютерами для внутреннего представления информации, которую они хранят. Компьютеры хранят множество различных типов информации, в том числе:
Мы иначе взаимодействуем с данными.Некоторые данные мы видим, другие данные, которые мы слушаем, и т. Д. Независимо от того, как мы взаимодействуем с данными, все типы информации, хранящейся в компьютере, хранятся внутри в одном и том же простом формате, последовательности нулей и единиц, известной как двоичный. Компьютеры используют числовые коды для представления всей информации, которую они хранят. Почему числа важны? Номера повсюду и связаны почти со всем, что мы делаем. Мы используем их для измерения лет, месяцев, недель, дней, часов и секунд.Считаем числа в долларах и центах. Мы измеряем числа в футах, дюймах, метрах и ярдах. Так что числа должны быть простыми. Верно? В конце концов, мы научились считать почти сразу, как научились говорить полными предложениями (возможно, даже раньше). Если бы я попросил вас выбрать два числа и только два числа, которые, по вашему мнению, являются самыми важными числами во всем мире, какое число вы бы выбрали? Вы бы выбрали 0 и 1 ? Возможно, лучший вопрос — почему числа важны для компьютеров? Числа — это наше прошлое, наше настоящее и наше будущее.Некоторые из ранних компьютеров были десятичными машинами, но современные компьютеры — двоичными машинами. Цифровой компьютер хранит информацию в виде чисел, но эти числа не хранятся в виде десятичных чисел. Числа внутри компьютера представлены в двоичной форме. Место хранения на компьютере не может быть пустым; он должен содержать либо 0, либо 1. Введение в системы счисления и двоичную систему :Все системы счисления работают по одним и тем же правилам.Базовое значение числовой системы сообщает нам, с каким количеством цифр нам нужно работать и каково значение каждой цифры в числе. Десятичная система счисления — это наиболее часто используемая и наиболее известная широкой публике система счисления. Она также известна как система нумерации Base 10 , поскольку она основана на 10 символах: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. В десятичной системе каждая цифра имеет свою собственную. положение, а также десятичная точка. Например, число 356.74 имеет 4 в позиции сотых, 7 в позиции десятых, 6 в позиции единиц, 5 в позиции десятков и 3 в позиции сотен. Десятичная система счисления также является одной из старейших известных систем счисления, которая исторически связана с индуистско-арабской системой счисления. Колода карточек, созданная Шеннон Андерсон-Раш с GoConqrЗадание: вопрос для размышления 3,2Направление: В чем важность числа 2 147 483 647? Числа повсюду и связаны практически со всем, что мы делаем (Intrieri, 2014).Какое значение имеет число 2 147 483 647? Используйте всемирную паутину и свои исследовательские навыки, чтобы найти ответ. Подготовьте короткое эссе (~ 150 слов) и приведите как минимум два примера, иллюстрирующих важность 2 147 483 647 слов. Убедитесь, что вы вычитали свой документ и вставили свое резюме прямо в текстовое поле. Не прикрепляйте отдельный документ или ссылку на свой Google Диск. Перечислите цитаты в конце и используйте цитаты в скобках внутри абзаца.Ваши цитаты должны быть в формате APA или MLA (простого URL-адреса недостаточно). Вы можете использовать http://www.easybib.com/, чтобы помочь вам с форматом цитирования. Если цитирование является онлайн-ссылкой, вы также должны указать дату доступа, которая, скорее всего, является сегодняшней датой. Пример Интриери Дж. (9 апреля 2014 г.), Почему числа так важны для нас? https://jeannieintrieri.com/2014/04/09/why-are-numbers-so-important-to-us/, дата обращения: 18 июня 2017 г.
Компьютеры представляют данные в виде наборов двоичных цифр. Представление состоит из битов, которые, в свою очередь, сгруппированы в более крупные наборы, например байты. «Двоичная — это простейшая система счисления, в которой используются только две цифры: 0 и 1. С помощью этих цифр вычислительные задачи могут быть решены машинами, потому что в цифровой электронике транзистор используется в двух состояниях. Эти два состояния могут быть представлены как 0 и 1.Вот почему эта система счисления является наиболее предпочтительной в современной компьютерной инженерии, а также среди специалистов по сетям и коммуникациям и других профессионалов. Основной язык компьютеров, двоичный код, все еще используется в современных машинах из-за его простого и элегантного дизайна. Двоичная — это система счисления Base two . Преобразование из десятичного числа в двоичное :Попрактикуемся.Можете ли вы преобразовать 34 10 в двоичную форму? Ответ: 100010 2 . Вы делаете математическое преобразование. Для чего-нибудь посложнее преобразуем 27 10 в десятичное число. Ответ: 11001 , но как я пришел к этому ответу? Присвоение: таблица преобразования десятичных чисел в двоичныеКак добраться: Загрузите рабочий лист преобразования десятичных чисел в двоичные. Преобразуйте двоичное число в десятичное.Вы должны показать свою работу (математику), чтобы получить зачет. Приложите отдельный лист со своей работой. «Только ответы» не приносят баллов. Введите свои ответы в рабочий лист itsLearning, а затем отправьте своему учителю фотографию своей математики (вы можете использовать камеру) Как преобразовать двоичное в десятичноеПопрактикуемся. Можете ли вы преобразовать 11101 2 в десятичную форму? Ответ: 29 10 . Вы делаете математическое преобразование. Для чего-нибудь посложнее преобразуем 11001 2 в десятичное.Ответ: 25 , но как я пришел к этому ответу? Присвоение: лист преобразования двоичного числа в десятичноеКак добраться: Загрузите таблицу преобразования двоичного числа в десятичное. Преобразуйте двоичное число в десятичное. Вы должны показать свою работу (математику), чтобы получить зачет. Не забывайте работать справа налево. Приложите отдельный лист со своей работой. Ответы приносят только нулевой балл. Введите свои ответы в рабочий лист itsLearning, а затем отправьте своему учителю фотографию своей математики (вы можете использовать камеру) Шестнадцатеричная или шестнадцатеричная система счисления с основанием 16.Эта система счисления особенно интересна, потому что в нашей обычно используемой десятичной системе есть только 10 цифр для представления чисел. Поскольку шестнадцатеричная система состоит из 16 цифр, дополнительные необходимые 6 цифр представлены первыми 6 буквами английского алфавита. Следовательно, шестнадцатеричные цифры — 0,1,2,3,4,5,6,7,8,9 и A, B, C, D, E, F. Эта система счисления чаще всего используется в математике и информационных технологиях. Например, в html-программировании цвета могут быть представлены шестизначным шестнадцатеричным числом: FFFFFF представляет белый цвет, 000000 представляет черный и так далее.При работе с цветами первые две цифры шестнадцатеричного числа представляют красный цвет, две средние цифры представляют значение зеленого цвета, а последние две цифры представляют интенсивность синего цвета. Шестнадцатеричная система счисления :Основная причина, по которой мы используем шестнадцатеричные числа, заключается в том, что гораздо легче выразить представление двоичных чисел в шестнадцатеричной системе, чем в любой другой системе счисления. Как преобразовать десятичное число в шестнадцатеричноеПреобразование из десятичного в шестнадцатеричное представление :Попрактикуемся.Можете ли вы преобразовать 65 10 в шестнадцатеричное? Ответ: 41 16 . Вы делаете математическое преобразование. Для чего-нибудь посложнее преобразуем 7 642 10 в шестнадцатеричное. Ответ: 1DDA , но как я пришел к такому ответу? Присвоение: таблица преобразования десятичных чисел в шестнадцатеричныеУказания: Загрузите рабочий лист преобразования десятичных чисел в шестнадцатеричные. Преобразуйте десятичное число в шестнадцатеричное.Вы должны показать свою работу (математику), чтобы получить зачет. Приложите отдельный лист со своей работой. Ответы приносят только нулевой балл. Введите свои ответы в рабочий лист itsLearning, а затем отправьте своему учителю фотографию своей математики (вы можете использовать камеру или сканер). Как преобразовать из шестнадцатеричного в десятичныйИтак, мы довольно хорошо научились преобразовывать десятичные числа в шестнадцатеричные, но как насчет преобразования в другом направлении. Обычное десятичное число — это сумма цифр, умноженная на 10 n .Вот пример: 137 по основанию 10 равно каждой цифре, умноженной на соответствующие 10 n : 137 10 = 1×10 2 + 3×10 1 + 7×10 0 = 100 + 30 + 7 шестнадцатеричных чисел читаются так же, но каждая цифра насчитывает 16 n вместо 10 n . Умножьте каждую цифру шестнадцатеричного числа на соответствующие 16 n . Давайте попробуем. Преобразуем B92F 16 в десятичную форму и посмотрим, что у нас получится.Помните, что шестнадцатеричное число B равно 11 в десятичном виде, а шестнадцатеричное F равно 15 в десятичном.
Теперь ваша очередь попробовать.Преобразуйте DC77 (шестнадцатеричное) в десятичное. Перед тем, как проверить здесь свой ответ, выполните вычисления. Вы правильно поняли? Назначение: таблица преобразования шестнадцатеричного числа в десятичноеКак добраться: Загрузите таблицу преобразования шестнадцатеричного числа в десятичное. Преобразуйте шестнадцатеричное число в десятичное. Вы должны показать свою работу (математику), чтобы получить зачет. Приложите отдельный лист со своей работой. «Только ответы» не приносят баллов. Введите свои ответы в рабочий лист itsLearning, а затем отправьте своему учителю фотографию своей математики (вы можете использовать камеру или сканер). Колода карточек, созданная Шеннон Андерсон-Раш с GoConqrЗадание: вопрос для размышления 3.3Маршрут: Погодите! Есть еще системы счисления, кроме двоичной, десятичной и шестнадцатеричной? Да это так. Другая система нумерации — Octal . Проведите небольшое исследование, чтобы выяснить, что такое восьмеричная система счисления. Для чего его используют? Сравните и сопоставьте четыре системы счисления: двоичную, восьмеричную, десятичную, шестнадцатеричную.Подготовьте короткое эссе (~ 75 слов). Убедитесь, что вы вычитали свой документ и вставили свое резюме прямо в текстовое поле. Не прикрепляйте отдельный документ.
Текстовый документ можно разбить на абзацы, предложения, слова и даже отдельные символы. Текстовый документ представлен в цифровой форме, представляя все возможные символы. Каждый отдельный символ — это цифровой элемент, который представлен и хранится в памяти компьютера.Существует ограниченное количество символов, которые можно представить в виде набора символов. Набор символов — это просто список символов и кодов, используемых для представления каждого из них. Два общих набора символов — это ASCII (произносится как ass-kee) и Unicode. ASCIIASCII — это американский стандартный код для обмена информацией. Первоначально в ASCII для представления каждого символа использовалось семь битов, что позволяло использовать 128 уникальных символов, при этом восьмой бит зарезервирован как контрольный бит для обеспечения правильной передачи данных.Сегодня расширенный ASCII Latin-1 использует все восемь битов и позволяет использовать 256 символов, а также включает буквы с диакритическими знаками и несколько специальных символов. Можете ли вы расшифровать сообщение ниже? Он написан в двоичном формате, и вам нужно будет использовать таблицу ASCII, чтобы преобразовать его в глиф. 100 1101 111 0010 111 0011010 1111 010 0000 101 0010 111 0101 111 0011 110 1000 010 0000 110 1001 111 0011 010 0000 110 1101 111 1001010 0000 111 0100110 0101 110 0001 110 0011110 1000110 0101 111 0010010 0001 ЮникодРасширенная версия набора символов ASCII содержит 256 символов, которых достаточно для английского языка, но недостаточно для международного использования.Набор символов Unicode имеет гораздо более сильное международное влияние. Цель Unicode — представить каждый символ на всех языках, используемых во всем мире, включая все азиатские идеограммы. Он также может представлять множество специальных символов, таких как научные символы. Первые 256 символов Unicode соответствуют 256 символам ASCII в расширенном наборе. Вы можете увидеть множество символов Юникода, посетив http://unicode-table.com/en/#control-character. Практика: Ваше имя в таблице ASCIIКак добраться: Напечатайте свое имя и фамилию. Используйте приведенную выше таблицу ASCII, чтобы теперь записать свое имя и фамилию в двоичном формате. Помните, что ваше имя и фамилия начинаются с заглавной буквы.
Компьютеры создают изображения, размещая на мониторе крошечные точки света, называемые пикселями. Пиксель означает «элемент изображения». Если вы внимательно посмотрите на монитор или воспользуетесь увеличительным стеклом, вы сможете увидеть отдельные пиксели.Цифровое изображение не имеет физической структуры. Конкретный способ, которым компьютер хранит данные изображения, называется форматом изображения. Слушайте, как соучредитель Instagram объясняет, как изображения представлены в двоичном формате и как фильтры изображений работают внутри.
Растровая графикаРастровая графика, также известная как растровая графика, хранит информацию о цвете и местоположении в прямоугольной сетке пикселей, составляющих графику.Размеры растровой графики — это количество пикселей в прямоугольной сетке. Например, если изображение имеет размер 800 x 600 пикселей, оно содержит 800 x 600 пикселей (или 480 000 отдельных пикселей). Мы измеряем качество растровой графики в количестве пикселей на дюйм или точек на дюйм. Другое название качества изображения — разрешение. Когда вы увеличиваете размер растровой графики, то же количество пикселей занимает больше места, и у вас меньше пикселей на дюйм.В результате изображение будет менее детализированным (с меньшим разрешением). Когда вы уменьшаете размер растровой графики, это дает противоположный эффект. Разрешение изображения увеличивается. При увеличении растрового изображения пиксели растягиваются. Два чемодана на этой веб-странице — это один и тот же файл изображения; однако чемодан справа был увеличен с помощью атрибута ширины HTML. Чемодан справа имеет нечеткий вид, потому что пиксели были растянуты, чтобы изображение выглядело больше.Мы называем это явление «пиксельным». Два очень популярных растровых изображения — это .GIF (произносится как Jiff или Giff) и .JPG (произносится как j-peg). Файлы GIF или «Формат обмена графикой»
JPEG или JPG или «Joint Photographic Experts Group»
Компьютерные программы, которые помогают создавать растровую графику, включают Adobe Photoshop, Microsoft Paint и любые программы для редактирования цифровых фотоаппаратов или фотографий. Векторная графикаВы когда-нибудь копировали изображение из Интернета и обнаруживали, что оно слишком мало для ваших нужд? Когда вы увеличиваете изображение, изображение, вероятно, искажается и пикселируется, как на чемоданах выше.Чтобы решить эту проблему, была создана векторная графика, и основным преимуществом векторной графики является то, что она не пикселизируется. Вы не можете растягивать пиксели, потому что нет пикселей. Векторная графика иногда называется рисованной графикой. Разработанная специально для использования на веб-страницах, векторная графика представляет изображение в виде геометрической формы, состоящей из прямых линий, овалов и дуг В векторной графике информация об изображениях хранится с использованием линий, форм и цветов, представленных математическими уравнениями.Поскольку они используют формы и математику для описания изображений, вы можете увеличивать или уменьшать векторную графику, не влияя на качество изображения. Векторная графика отлично подходит для иллюстраций, логотипов, кнопок, фигур и даже некоторых более сложных типов графики и текста. Для чего они не подходят, так это для фотографий. Это связано с тем, что фотографии содержат так много деталей, что с точки зрения размера файла преобразовывать их в линии и формы неэкономично. Компьютерные программы, работающие с векторной графикой, включают Adobe Illustrator, CorelDraw и любые другие приложения для создания иллюстраций. Когда дело дошло до Интернета, растровая графика была единственной игрой в городе, но не более! Последнее поколение веб-браузеров (включая Chrome, Safari и большинство мобильных браузеров) содержит встроенную поддержку масштабируемой векторной графики (SVG). SVG — это широко распространенный бесплатный графический формат, разработанный и поддерживаемый рабочей группой W3C SVG. SVG — это словарь XML, который можно использовать для описания компьютерной графики. Компьютерная программа (например, браузер), которая знает, как интерпретировать SVG, использует код для отображения изображений. Назначение: Инфографика технических новостейНаправления: Найдите статью о новой технологии и создайте инфографику (вычислительный артефакт). В инфографике будут использованы творческие идеи, чтобы донести информацию в новостной статье информативным образом. Можно использовать некоторый текст (подписи, маркеры), но это не является в первую очередь текстовым созданием. Используйте изображения, графику и другие важные элементы, которые сообщают Новости, чтобы другие хотели узнать информацию в вашей статье.Найдите в своей статье что-нибудь, связанное с данными, и объясните или создайте для этого диаграмму. Загрузите полные инструкции и рубрику с сайта itsLearning. АудиоКомпьютеры представляют звук в цифровом виде, применяя к определенным образцам звука число. Системы цифровых аудиотехнологий используют двоичную систему счисления для хранения и распространения информации. Решения и операции в цифровой системе принимаются с помощью булевой алгебры, и это очень быстрый и эффективный способ работы цифровых устройств.Это делается путем выборки исходной функции каждые несколько моментов времени (заданная частота, называемая частотой выборки). Звук не может быть дискретизирован непрерывно, потому что это займет огромное количество памяти. Таким образом, каждый образец представлен в виде числа для экономии памяти.
Основным устройством, используемым в цифровой записи, является аналого-цифровой преобразователь (АЦП). АЦП делает снимок электрического напряжения на аудиолинии, который затем представляется в виде цифрового числа, понятного компьютеру.Регистрируя напряжение тысячи раз в секунду, вы можете получить очень хорошее приближение к исходному звуковому сигналу. Поскольку аудиофайлы должны быть высокого качества, для них может потребоваться много места в памяти. Звуковые файлы могут быть очень большими, поэтому файлы могут быть сжаты. Есть два типа сжатия: с потерями и без потерь.
Аудио хранится в виде семплов, расположенных через определенные интервалы. Чем меньше эти промежутки, тем выше будет качество аудиофайла. Наивысшая обычно используемая частота дискретизации составляет 44,1 кГц, что соответствует качеству компакт-диска, но это означает, что у него будет довольно большой размер файла. Нет смысла использовать более высокую частоту дискретизации, потому что люди могут слышать только частоты от 0 до 20 кГц, поэтому этого качества достаточно. Вы можете узнать больше о цифровом аудио, посетив «Как работают цифровые аудиотехнологии» Рича Уильямса. За последние несколько лет стали популярными несколько форматов аудиоданных. Эти форматы включают WAV, AU, IFF, VQF и MP3. Эти форматы основаны на этапе выборки значений напряжения из аналоговых сигналов, но все они распознают детали данных по-разному, и все в той или иной степени используют различные методы сжатия. ВидеоВидеоинформация — это один из самых сложных типов информации, который нужно захватывать, сжимать и при этом получать в результате, понятном человеческому глазу.Видео и анимация на самом деле являются иллюстрацией, которая обманывает глаз и мозг, заставляя думать, что есть движение. Цифровое видео — это представление движущихся визуальных образов в виде закодированных цифровых данных. Цифровое видео представляет собой серию ортогональных растровых цифровых изображений, отображаемых в быстрой последовательности с постоянной скоростью. Видео кодируется с помощью программного обеспечения под названием кодек (enCOder / DECoder). Видео кодируется для целей хранения, поскольку видеофайлы могут иметь очень большой размер, поэтому для сжатия файла используется программное обеспечение, чтобы уменьшить его.Кодек не только сжимает файл, но и сохраняет его в определенном формате. Это программное обеспечение также может распаковать файл во время его воспроизведения. Один из самых распространенных форматов файлов — это AVI, но есть и многие другие, например MPEG. Различные методы кодеков включают XviD и DivX. Ошибки при передаче битовТот факт, что данные являются цифровыми, не означает, что они не содержат ошибок. Биты информации, передаваемые через различные носители, могут поступать неверно из-за:
Обнаружение ошибокОбнаружение ошибок — это обнаружение ошибок, вызванных шумом или другими помехами во время передачи от передатчика к приемнику. Обнаружение ошибок: добавление четностиБиты четности обеспечивают простейший метод исправления ошибок. Четность — это свойство быть четным или нечетным. Тот факт, что все числа имеют четность, обычно используется при передаче данных для обеспечения достоверности данных. Предположим, например, что два устройства обмениваются данными с проверкой четности (наиболее распространенная форма проверки четности). Когда передающее устройство отправляет данные, оно подсчитывает количество установленных битов в каждой группе из семи битов.Если количество установленных битов четное, он устанавливает бит четности в 0; если количество установленных битов нечетное, бит четности устанавливается равным 1. Таким образом, каждый байт имеет четное количество установленных битов. На принимающей стороне устройство проверяет каждый байт, чтобы убедиться, что он имеет четное количество установленных битов. Если он обнаруживает нечетное количество установленных битов, получатель знает, что во время передачи произошла ошибка. Отправитель и получатель должны согласиться использовать проверку четности и договориться о том, должна ли четность быть четной или нечетной.Если две стороны не настроены с одинаковым контролем четности, связь будет невозможна. http://www.webopedia.com/TERM/P/parity_checking.html
Исправление ошибокИсправление ошибок — это обнаружение ошибок и восстановление исходных безошибочных данных. Многие из основных механизмов вычислений прозрачны для большинства пользователей. Например, отправка текстового сообщения или электронного письма может привести к повторной доставке в случае ошибки передачи, но пользователь может не знать о необходимости повторной отправки сообщения — оно отправляется повторно без необходимости знать об ошибке. Набор слайдов, созданный Шеннон Андерсон-Раш с GoConqr Университет Теннесси, основы вычислений: http://web.eecs.utk.edu/research/cs100modules/copyright.html Полевое руководство по информатике: 5. Представление данных: http://www. |

 Затем неполное
частное, полученное от такого деления,
нужно снова разделить с остатком на
Затем неполное
частное, полученное от такого деления,
нужно снова разделить с остатком на 
 Таких элементов достаточно много: намагниченный или не намагниченный сердечник, открытый или закрытый транзистор и др. Для десятичной системы счисления понадобилось бы, к примеру, устройство с 10 устойчивыми состояниями. Это значительно усложнило бы схему ЭВМ.
Таких элементов достаточно много: намагниченный или не намагниченный сердечник, открытый или закрытый транзистор и др. Для десятичной системы счисления понадобилось бы, к примеру, устройство с 10 устойчивыми состояниями. Это значительно усложнило бы схему ЭВМ.  Отметим недостаток, характерный для двоичной системы счисления — значительный рост числа разрядов при увеличении числа. Но все достоинства этой системы делают такой недостаток не столь существенным.
Отметим недостаток, характерный для двоичной системы счисления — значительный рост числа разрядов при увеличении числа. Но все достоинства этой системы делают такой недостаток не столь существенным. 

 Каждая цифра в компьютере — это электрический сигнал. Двоичная система управляет компьютерными операциями, позволяя току проходить через схемы во включенном состоянии и останавливая ток в выключенном состоянии.Цифровые логические схемы используют напряжение нуля для представления двоичной цифры 0 и напряжение в пять вольт для представления двоичной цифры 1. Двоичные системы предоставляют дискретные значения, с которыми легко работать, в отличие от аналоговых уровней напряжения, с которыми трудно работать. с в компах.
Каждая цифра в компьютере — это электрический сигнал. Двоичная система управляет компьютерными операциями, позволяя току проходить через схемы во включенном состоянии и останавливая ток в выключенном состоянии.Цифровые логические схемы используют напряжение нуля для представления двоичной цифры 0 и напряжение в пять вольт для представления двоичной цифры 1. Двоичные системы предоставляют дискретные значения, с которыми легко работать, в отличие от аналоговых уровней напряжения, с которыми трудно работать. с в компах. Но этот вопрос также часто задают люди, не особо разбирающиеся в технологиях. Так или иначе,
Ответ довольно прост.
Но этот вопрос также часто задают люди, не особо разбирающиеся в технологиях. Так или иначе,
Ответ довольно прост. .. подробнее об этом позже).
.. подробнее об этом позже).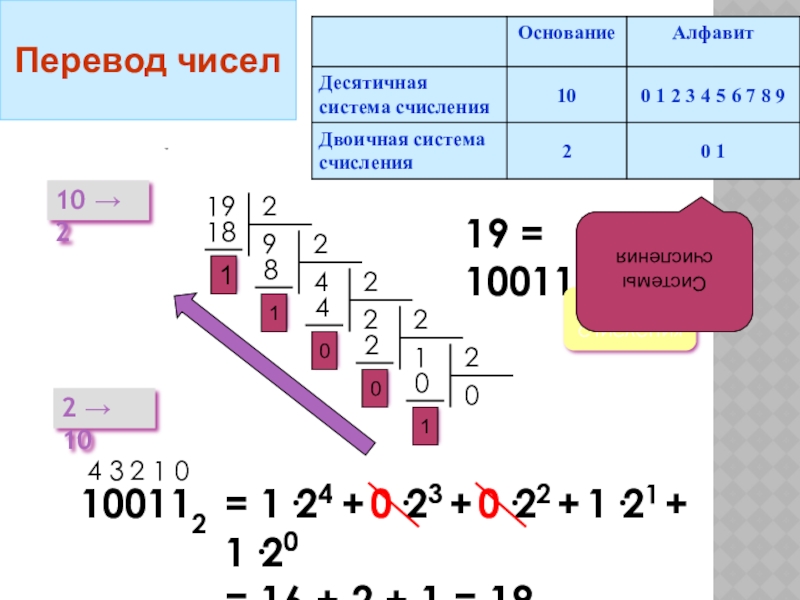 который может надежно удерживать более двух возможных состояний.(Квантовые компьютеры не совсем
продажа на данный момент.)
Бинарная система была выбрана только потому, что в ней достаточно легко различить наличие
электрический ток от отсутствия электрического тока, особенно при работе с триллионами
таких подключений. И используя любую другую систему счисления в этой системе
смешно, потому что системе нужно было бы постоянно конвертировать между ними.
Это все, что нужно сделать.
который может надежно удерживать более двух возможных состояний.(Квантовые компьютеры не совсем
продажа на данный момент.)
Бинарная система была выбрана только потому, что в ней достаточно легко различить наличие
электрический ток от отсутствия электрического тока, особенно при работе с триллионами
таких подключений. И используя любую другую систему счисления в этой системе
смешно, потому что системе нужно было бы постоянно конвертировать между ними.
Это все, что нужно сделать.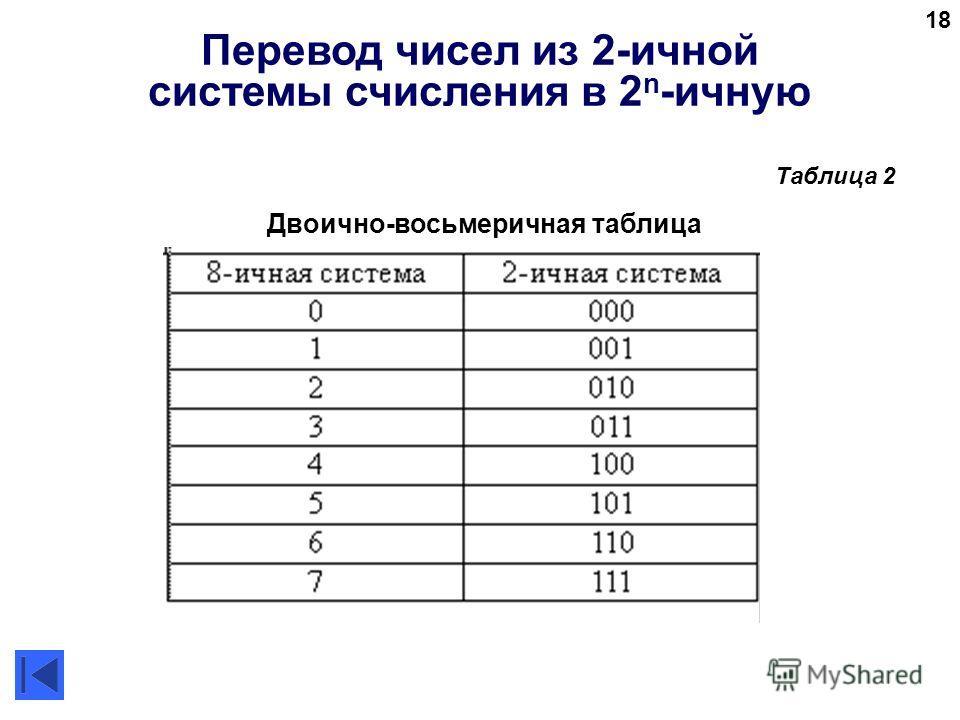 э. в Египте и в 3000 г. до н.э.
в Месопотамии они разработали символ, представляющий единицу 10.
Это было большим достижением, поскольку уменьшило количество
обязательные символы. Например, 12 можно представить как 10
и два юнита (три символа вместо 12, что требовалось
ранее).
э. в Египте и в 3000 г. до н.э.
в Месопотамии они разработали символ, представляющий единицу 10.
Это было большим достижением, поскольку уменьшило количество
обязательные символы. Например, 12 можно представить как 10
и два юнита (три символа вместо 12, что требовалось
ранее). Например, десятичный
имеет основание из десяти значений от 0 до 9.
Например, десятичный
имеет основание из десяти значений от 0 до 9.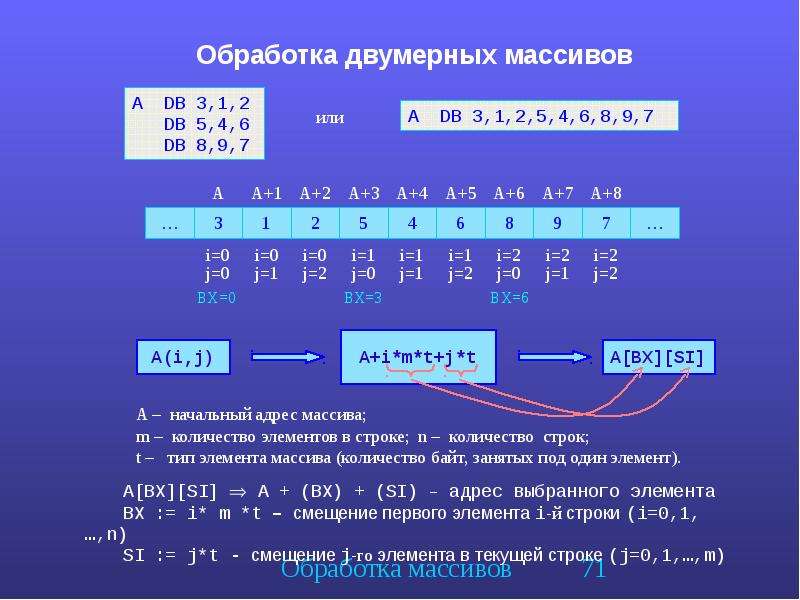 Другой пример добавления и превышения диапазона базовой установки
198 + 4
198
199 +1
200 +2 Примечание 2:
201 +3
202 +4
Примечание 2: при превышении 9 мы возвращаемся к началу набора (0),
и перенесите значение 1 в следующий столбец слева. Таким образом
в средний столбец (9) добавлен 1, следующее значение в наборе - 0, и
мы переносим 1 (потому что набор был превышен) в следующий левый столбец.Добавление
значение переноса от 1 до 1 в крайнем левом столбце дает.
Другой пример добавления и превышения диапазона базовой установки
198 + 4
198
199 +1
200 +2 Примечание 2:
201 +3
202 +4
Примечание 2: при превышении 9 мы возвращаемся к началу набора (0),
и перенесите значение 1 в следующий столбец слева. Таким образом
в средний столбец (9) добавлен 1, следующее значение в наборе - 0, и
мы переносим 1 (потому что набор был превышен) в следующий левый столбец.Добавление
значение переноса от 1 до 1 в крайнем левом столбце дает.
 значения 10.Это произошло потому, что было 10 значений (0–9) в
набор. В этой двоичной системе всего два значения (0 — 1)
в наборе, поэтому столбцы представляют собой значения умножения 2.
значения 10.Это произошло потому, что было 10 значений (0–9) в
набор. В этой двоичной системе всего два значения (0 — 1)
в наборе, поэтому столбцы представляют собой значения умножения 2.  1011
101
------
10000
1011
101
------
10000
 Иногда бывает
называется подходом 8: 4: 2: 1.
Иногда бывает
называется подходом 8: 4: 2: 1.  значения для представления чисел.Значения:
значения для представления чисел.Значения: 

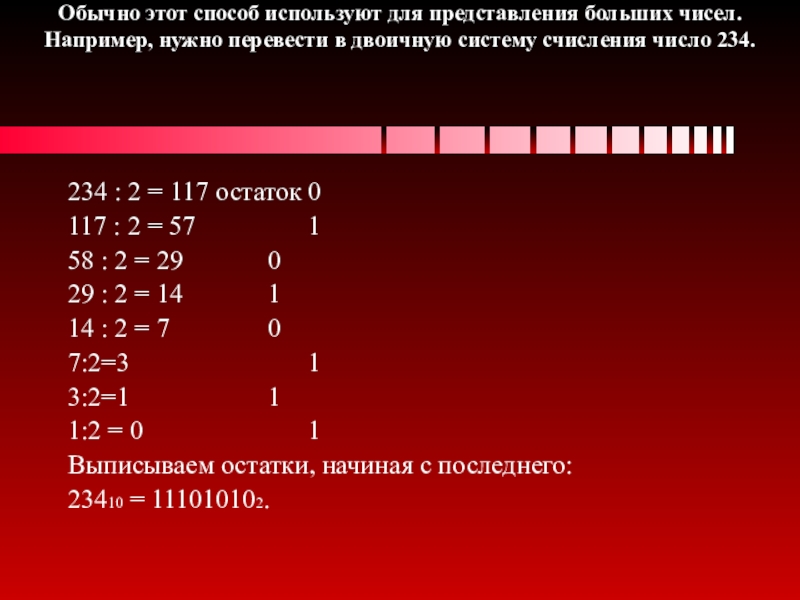 Скопируйте первую 1, затем инвертируйте все
оставшиеся биты.
Скопируйте первую 1, затем инвертируйте все
оставшиеся биты.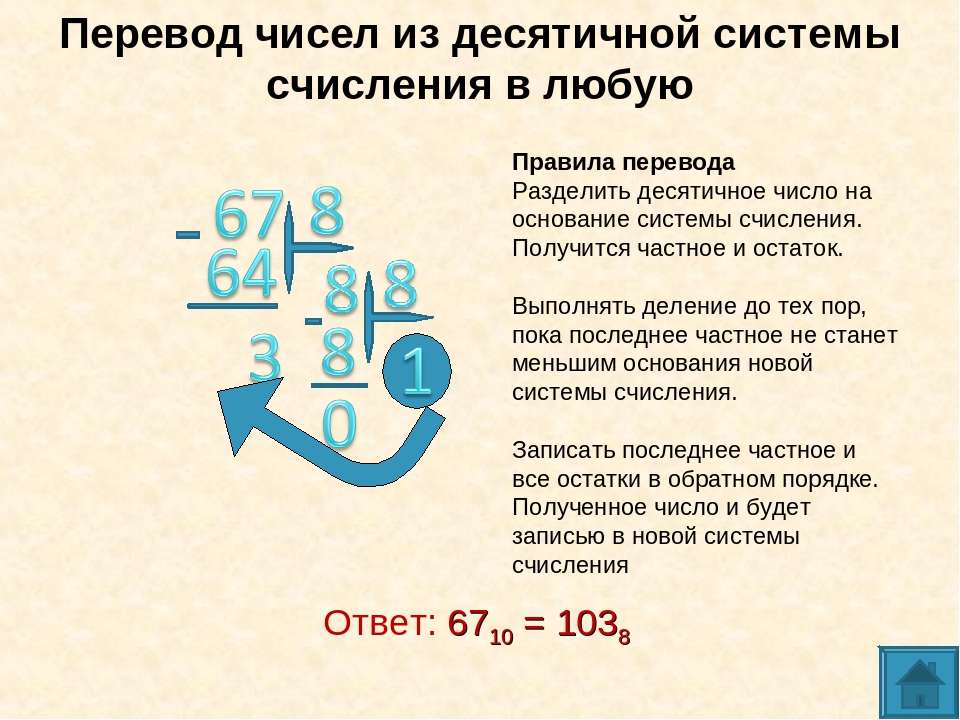 Это означает, что он устроен так
что каждый переход от одного значения к следующему включает
только одноразрядное изменение .
Это означает, что он устроен так
что каждый переход от одного значения к следующему включает
только одноразрядное изменение .
 10 01001 11 1 по модулю 2 0 = 1
4. 1 00 1001110 0 по модулю 2 0 = 0
3/4 10 01 001 1101 0 по модулю 2 1 = 1
3/4 100 10 01 11011 1 по модулю 2 0 = 1
3/4 1001 00 1 110110 0 по модулю 2 0 = 0
3/4 10010 01 1101101 0 по модулю 2 1 = 1
Ответ 1101101
10 01001 11 1 по модулю 2 0 = 1
4. 1 00 1001110 0 по модулю 2 0 = 0
3/4 10 01 001 1101 0 по модулю 2 1 = 1
3/4 100 10 01 11011 1 по модулю 2 0 = 1
3/4 1001 00 1 110110 0 по модулю 2 0 = 0
3/4 10010 01 1101101 0 по модулю 2 1 = 1
Ответ 1101101
 1984–1999 годы.
Все права защищены.
1984–1999 годы.
Все права защищены.  Например, в цифровом компьютере мы можем представить музыку как последовательность битов в mp3-файле, а в аналоговой системе мы можем представить музыку как волновой узор. Старомодные виниловые пластинки являются скорее хорошим примером аналогового носителя записи. чем представляют музыку через серию битов, бороздки на виниловой пластинке приблизительно соответствуют звуковым волнам, которые были записаны.
Например, в цифровом компьютере мы можем представить музыку как последовательность битов в mp3-файле, а в аналоговой системе мы можем представить музыку как волновой узор. Старомодные виниловые пластинки являются скорее хорошим примером аналогового носителя записи. чем представляют музыку через серию битов, бороздки на виниловой пластинке приблизительно соответствуют звуковым волнам, которые были записаны.