Информатика система счисления примеры: Основы систем счисления / Habr – 1.5 Преобразование чисел из одной системы счисления в другую.

Урок информатики в 9-м классе. Тема: «Системы счисления»

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Тип урока: Урок изучения новой темы.

Дидактическая цель: создать условия для актуализации и закрепления учебной информации

Цель урока:

Образовательная:

• знакомство с понятием «система счисления»;
• умение различать виды систем счисления и применять их на практическом занятии;
• умение правильно записывать числа в системах счисления;
• формирование способности для применения правил перевода чисел из одной системы счисления в другие.

Развивающая:

• развивать логическое мышление, умение обобщать, конкретизировать;
• формирование внимания, умения наблюдать и закреплять знания;

Воспитательная:

• воспитывать самостоятельность, уважительное отношение друг к друг;
• воспитание информационной культуры учащихся.

Методы обучения: наглядный, информационно-развивающий, опрос.

Формы организации познавательной деятельности: индивидуальная.

Средства обучения: учебник Семакина “Информатика и ИКТ. 9 класс. ” учебник для 9 класса общеобразовательных учреждений, рабочие тетради, авторучки, проектор, компьютер, компьютерная презентация по теме урока.

План урока:

1. Организационный момент.
2. Изучение нового материала.
3. Физкультминутка.
4. Формирование умений, навыков.
5. Домашнее задание

Ход урока

1. Организационный момент.

Приветствие, проверка присутствующих. Мы сегодня начинаем изучение новой темы. Данная тема очень важна. Хотелось бы отметить умение решать задачи на систему счисления дает возможность набрать более высокие баллы, что очень важно при сдаче ЕГЭ и поступлении в ВУЗЫ. Открываем тетрадки, записываем сегодняшнее число и тему: СИСТЕМЫ СЧИСЛЕНИЯ.

План темы

1. Историческая справка
2. Определение системы счисления
3. Виды системы счисления
4. Правила перевода чисел из одной системы счисления в другую

2. Объяснение нового материала (по плану, приложение 3)

2.1. Историческая справка

Люди научились считать еще в незапамятные времена. Сначала они просто различали один предмет перед ними или нет. Если предмет был не один, то говорили «много». Постепенно появилось слово для обозначения двух предметов. Счет парами очень удобен.

Наиболее древней и простой «счетной машиной» издавна являются пальцы рук и ног. И даже в наше время еще пользуются этим «счетным прибором», который всегда при нас. На пальцах можно решать примеры не только в пределах десяти. В древние времена люди ходили босиком. Поэтому они могли пользоваться для счета пальцами как рук, так и ног.

Записывали числа поначалу совсем просто: делали зарубки на куске дерева или кости. На этой кости тридцать тысяч лет назад сделаны нарезки, они показывают, что уже тогда наши предки умели не только считать, но и записывать результаты счета!

Когда понадобилось записывать большие числа, то для пятерок и десяток стали придумывать новые знаки. Вот как египтяне записывали число 3 246: 

Запомнить большие числа трудно, поэтому к «счетной машине» рук и ног добавляли механические приспособления. Веревочные счеты с узелками применялись и в России, и во многих странах Европы. Остатками этого способа является практикуемое еще до сих пор завязывание узелков на носовых платках «на память». Так, одни пользовались для запоминания чисел камешками, зернами, веревкой с узелками, другие — палочками с зарубками. Это были первые счетные приборы, которые в конце концов привели к образованию различных систем счисления

2.2. Система счисления — это совокупность правил и приемов записи чисел с помощью набора цифровых знаков.

• позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
• непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.

Непозиционные СС. Единичная система счисления. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): зарубок, черточек, точек. Позже значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня (счетные палочки для обучения счету; полоски, нашитые на рукаве, означают на каком курсе учится курсант военного училища). Неудобства такой системы записи чисел и ограниченность ее применения очевидны: чем большее число надо записать, тем длиннее строка из палочек.

Римская система счисления является непозиционной системой. В ней для записи чисел используются буквы латинского алфавита. При записи чисел в римской системе счисления значением числа является алгебраическая сумма цифр, в него входящих. При этом цифры в записи числа следуют, как правило, в порядке убывания их значений, и не разрешается записывать рядом более трех одинаковых цифр. В том случае, когда за цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в целом является отрицательным. Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.

Таблица 1. Запись чисел в римской системе счисления

1	2	3	4	5	6	7	8	9	10	50	100	500	1000
I	II	III	IV	V	VI	VII	VIII	IX	X	L	C	D	M

Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами. По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.

Мы с вами более подробно рассмотрим позиционные системы счисления.

В позиционной системе счисления основными понятиями являются понятие алфавита и основания системы счисления.

Алфавитом системы счисления называется совокупность всех цифр.

Количество цифр, необходимых для записи числа в системе, называют основанием  системы счисления. Основание системы записывается в справа числа в нижнем индексе: 78₁₀, 1100010₁₂, AF12₁₆ и т. д.

Количество цифр, составляющих алфавит, называется его мощностью.

В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места(разряда), где он расположен. Разряд — номер позиции в числе. Нумеруются справа налево, начиная с нуля.

Пример. Число6184₁₀ запишется в форме многочлена следующим образом:

6184₁₀ = 6*10 ³ +1*10 ² +8*10 ¹ +4*10 ⁰

2.3. Виды систем счисления.

В компьютерах принято использовать 4 основные системы счисления – двоичную, восьмеричную, десятичную и шестнадцатеричную. Именно их подробно рассмотрим.

Десятичная система счисления – в настоящее время наиболее известная и используемая. Древнее изображение десятичных цифр не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 — углов нет, 1 — один угол, 2 — два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.

Десятичная система впервые появилась в Индии примерно в VI веке новой эры. Индийская нумерация использовала девять числовых символов и нуль для обозначения пустой позиции

Десятичная система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.

Если взять правило, по которым строятся числа в десятичной системе счисления, заменив основание 10 на натуральное число N, можно построить позиционную систему счисления с основанием N.

В вычислительных машинах используется двоичная система счисления, её основание — число 2. Для записи чисел в этой системе используют только две цифры — 0 и 1. Двоичная система счисления была придумана математиками и философами задолго до появления компьютеров, еще в ХVII — ХIХ веках. Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной — восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост. Ниже приведена таблица соответствия чисел, записанных в разных системах.

Учащиеся заполняют таблицу в тетрадях (приложение 1, таблица 1).

2.4. Правила перевода чисел из одной системы счисления в другую

Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.

1. При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

Числа 10100110₂ , 703₈ , 23FA1₁₆ перевести в десятичную систему счисления.

10100110₂=1*2⁷+0*2⁶+1*2⁵+0*2⁴+0*2³+1*2²+1*2¹+0*2⁰=128+32+4+2=166₁₀

703₈=7*8²+0*8¹+3*8⁰=448+3=447₁₀

23FA1₁₆=2*16⁴+3*16³+15*16²+10*16¹+1*16⁰=131072+12288+3840+160+1=147361

2. Правило перевода из десятичной системы счисления в систему с основанием q:

1. Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.

2. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).

Пример. Перевести числа из десятичной системы счисления

3. Чтобы перевести число из двоичной системы в восьмеричную (шестнадцатеричную), его нужно разбить на триады (тетрады), начиная с младшего разряда (справа налево), в случае необходимости дополнив старшую триаду (тетраду) нулями, и каждую триаду (тетраду) заменить соответствующей восьмеричной (шестнадцате

Системы счисления | Информатика

Совокупность приемов записи и наименования чисел называется системой счисления.

Числа записываются с помощью символов, и по количеству символов, используемых для записи числа, системы счисления подразделяются на позиционные и непозиционные. Если для записи числа используется бесконечное множество символов, то система счисления называется непозиционной. Примером непозиционной системы счисления может служить римская. Например, для записи числа один используется буква I, два и три выглядят как совокупности символов II, III, но для записи числа пять выбирается новый символ V, шесть — VI, десять — вводится символ X, сто — С, тысяча — Ми т.д. Бесконечный ряд чисел потребует бесконечного числа символов для записи чисел. Кроме того, такой способ записи чисел приводит к очень сложным правилам арифметики.

Позиционные системы счисления для записи чисел используют ограниченный набор символов, называемых цифрами, и величина числа зависит не только от набора цифр, но и от того, в какой последовательности записаны цифры, т.е. от позиции, занимаемой цифрой, например, 125 и 215. Количество цифр, используемых для записи числа, называется основанием системы счисления, в дальнейшем его обозначим q.

В повседневной жизни мы пользуемся десятичной позиционной системой счисления, q = 10, т.е. используется 10 цифр: 0 1 2 3 4 5 6 7 8 9.

Рассмотрим правила записи чисел в позиционной десятичной системе счисления. Числа от 0 до 9 записываются цифрами, для записи следующего числа цифры не существует, поэтому вместо 9 пишут 0, но левее нуля образуется еще один разряд, называемый старшим, где записывается (прибавляется) 1, в результате получается 10. Затем пойдут числа 11, 12, но на 19 опять младший разряд заполнится и мы его снова заменим на 0, а старший разряд увеличим на 1, получим 20. Далее по аналогии 30, 40 … 90, 91, 92 … до 99. Здесь заполненными оказываются два разряда сразу; чтобы получить следующее число, мы заменяем оба на 0, а в старшем разряде, теперь
уже третьем, поставим 1 (т.е. получим число 100) и т.д. Очевидно, что, используя конечное число цифр, можно записать любое сколь угодно большое число. Заметим также, что производство арифметических действий в десятичной системе счисления весьма просто.

В информатике, вследствие применения электронных средств вычислительной техники, большое значение имеет двоичная система счисления, q = 2. На ранних этапах развития вычислительной техники арифметические операции с действительными числами производились в двоичной системе ввиду простоты их реализации в электронных схемах вычислительных машин. Например, таблица
сложения и таблица умножения будут иметь по четыре правила:

0 + 0 = 0	0x0 = 0
0+1 = 1	0x1=0
1+0=1	1×0 = 0
1 + 1 = 10	1×1 = 1

А значит, для реализации поразрядной арифметики в компьютере потребуются вместо двух таблиц по сто правил в десятичной системе счисления две таблицы по четыре правила в двоичной. Соответственно на аппаратном уровне вместо двухсот электронных схем —восемь.

Но запись числа в двоичной системе счисления длиннее записи того же числа в десятичной системе счисления в log₂ 10 раз (примерно в 3,3 раза). Это громоздко и не удобно для использования, так как обычно человек может одновременно воспринять не более пяти-семи единиц информации, т.е. удобно будет пользоваться такими системами счисления, в которых наиболее часто используемые числа (от единиц до тысяч) записывались бы одной-четырьмя цифрами.
Как это будет показано далее, перевод числа, записанного в двоичной системе счисления, в восьмеричную и шестнадцатеричную очень сильно упрощается по сравнению с переводом из десятичной в двоичную. Запись же чисел в них в три раза короче для восьмеричной и в четыре для шестнадцатеричной системы, чем в двоичной, но длины чисел в десятичной, восьмеричной и шестнадцатеричной системах счисления будут различаться ненамного. Поэтому, наряду с двоичной системой счисления, в информатике имеют хождение восьмеричная и шестнадцатеричная системы счисления.

Восьмеричная система счисления имеет восемь цифр: 0 12 3 4 5 6 7. Шестнадцатеричная — шестнадцать, причем первые 10 цифр совпадают по написанию с цифрами десятичной системы счисления, а для обозначения оставшихся шести цифр применяются большие латинские буквы, т.е. для шестнадцатеричной системы счисления получим набор цифр: 0123456789ABCDEF.

Если из контекста не ясно, к какой системе счисления относится запись, то основание системы записывается после числа в виде нижнего индекса. Например, одно и то же число 231, записанное в
десятичной системе, запишется в двоичной, восьмеричной и шестнадцатеричной системах счисления следующим образом:

231₀₀₎= 111001 ll₍₂₎= 347_(g)=E7₍₁₆₎.

Запишем начало натурального ряда в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.

Десятичная	Двоичная	Восьмерич-	Шестнадцате-
		ная	ричная
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5

 

Десятичная	Двоичная	Восьме- ричная	Шестнадца- теричная
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	А
11	1011	13	В
12	1100	14	С
13	1101	15	D
14	1110	16	Е
15	1111	17	F
16	10000	20	10
17	10001	21	11

Лекция по информатике «системы счисления»

система счисления — это система записи чисел, в которой используется специальный алфавит или определенный набор цифр.

В зависимости от того, меняется ли значение цифры от ее положения в числе, выделяют две: позиционную и непозиционную системы счисления.

В позиционных системах значение цифры меняется вместе с ее положением в числе. Так, если взять число 234, то цифра 4 в ней означает единицы, если же рассмотреть число 243, то тут она будет уже означать десятки, а не единицы.

В непозиционных системах значение цифры статично, вне зависимости от ее положения в числе. Наиболее яркий пример – палочковая система, где каждая единица обозначается с помощью черточки. Неважно, куда вы припишите палочку, значение числа измениться лишь на единицу.

Непозиционные системы

К непозиционным системам счисления относятся:

Единичная система, которая считается одной из первых. В ней вместо цифр использовались палочки. Чем их было больше, тем больше было значение числа. Встретить пример чисел, записанных таким образом, можно в фильмах, где речь идет о потерянных в море людях, заключенных, которые отмечают каждый день с помощью зарубок на камне или дереве.

Римская, в которой вместо цифр использовались латинские буквы. Используя их, можно записать любое число. При этом его значение определялось с помощью суммы и разницы цифр, из которых состояло число. Если слева от цифры находилось меньшее число, то левая цифра вычиталась из правой, а если справа цифра была меньше или равна цифре слева, то их значения суммировались. Например, число 11 записывалось как XI, а 9 – IX.

Буквенные, в которых числа обозначались с помощью алфавита того или иного языка. Одной из них считается славянская система, в которой ряд букв имел не только фонетическое, но и числовое значение.

Вавилонская система счисления,в которой использовалось всего два обозначения для записи – клинья и стрелочки.

В Египте тоже использовались специальные символы для обозначения чисел. При записи числа каждый символ мог использоваться не более девяти раз.

Позиционные системы

Большое внимание уделяется в информатике позиционным системам счисления. К ним относятся следующие:

двоичная;

восьмеричная;

десятичная;

шестнадцатеричная;

шестидесятеричная, используемая при счете времени (к примеру, в минуте — 60 секунд, в часе — 60 минут).

Каждая из них обладает своим алфавитом для записи, правилами перевода и выполнения арифметических операций.

Десятичная система

Данная система является для нас наиболее привычной. В ней используются цифры от 0 до 9 для записи чисел. Они также носят название арабских. В зависимости от положения цифры в числе, она может обозначать разные разряды – единицы, десятки, сотни, тысячи или миллионы. Ее мы пользуемся повсеместно, знаем основные правила, по которым производятся арифметические операции над числами.

Двоичная система

Одна из основных систем счисления в информатике – двоичная. Ее простота позволяет компьютеру производить громоздкие вычисления в несколько раз быстрее, нежели в десятичной системе.

Для записи чисел используется лишь две цифры – 0 и 1. При этом, в зависимости от положения 0 или 1 в числе, его значение будет меняться.

Изначально именно с помощью двоичного кодакомпьютеры получали всю необходимую информацию. При этом, единица означала наличие сигнала, передаваемого с помощью напряжения, а ноль – его отсутствие.

Восьмеричная система

Еще одна известная компьютерная система счисления, в которой применяются цифры от 0 до 7. Применялась в основном в тех областях знаний, которые связаны с цифровыми устройствами. Но в последнее время она употребляется значительно реже, так как на смену ей пришла шестнадцатеричная система счисления.

Двоично-десятичная система

Представление больших чисел в двоичной системе для человека – процесс довольно сложный. Для его упрощения была разработана двоично-десятичная система счисления.Используется она обычно в электронных часах, калькуляторах. В данной системе из десятичной системы в двоичную преобразуется не все число, а каждая цифра переводится в соответствующий ей набор нулей и единиц в двоичной системе. Аналогично происходит и перевод из двоичной системы в десятичную. Каждая цифра, представленная в виде четырехзначного набора нулей и единиц, переводится в цифру десятичной системы счисления. В принципе, нет ничего сложного.

Для работы с числам в данном случае пригодится таблица систем счисления, в которой будет указано соответствие между цифрами и их двоичным кодом.

Шестнадцатеричная система

В последнее время все большую популярность приобретает в программировании и информатике система счисления шестнадцатеричная. В ней используются не только цифры от 0 до 9, но и ряд латинских букв – A, B, C, D, E, F.

При этом, каждая из букв имеет свое значение, так A=10, B=11, C=12 и так далее. Каждое число представляется в виде набора из четырех знаков: 001F.

Перевод чисел: из десятичной в двоичную

Перевод в системах счисления чисел происходит по определенным правилам. Наиболее часто встречается перевод из двоичной в десятичную систему и наоборот.

Для того, чтобы перевести число из десятичной системы в двоичную, необходимо последовательно делить его на основание системы счисления, то есть, число два. При этом, остаток от каждого деления необходимо фиксировать. Так будет происходить до тех пор, пока остаток от деления не будет меньше или равен единице. Проводить вычисления лучше всего в столбик. Затем полученные остатки от деления записываются в строку в обратном порядке.

Например, переведем число 9 в двоичную систему:

Делим 9, так как число не делится нацело, то берем число 8, остаток будет 9 – 1 = 1.

После деления 8 на 2 получаем 4. Снова делим его, так как число делится нацело – получаем в остатке 4 – 4 = 0.

Проводим ту же операцию с 2. В остатке получаем 0.

В итоге деления у нас получается 1.

Далее записываем все полученные нами остатки в обратном порядке, начиная с итога деления: 1001.

Вне зависимости от итоговой системы счисления, перевод чисел из десятичной в любую другую будет происходить по принципу деления числа на основу позиционной системы.

Перевод чисел: из двоичной в десятичную

Довольно легко переводить числа и в десятичную систему счисления из двоичной. Для этого достаточно знать правила возведения чисел в степень. В данном случае, в степень двойки.

Алгоритм перевода следующий: каждую цифру из кода двоичного числа необходимо умножить на двойку, причем, первая двойка будет в степени m-1, вторая – m-2 и так далее, где m – количество цифр в коде. Затем сложить результаты сложения, получив целое число.

Для школьников этот алгоритм можно объяснить проще:

Для начала берем и записываем каждую цифру, умноженную на двойку, затем проставляем степень двойки с конца, начиная с нуля. Потом складываем полученное число.

Для примера разберем с вами полученное ранее число 1001, переведя его в десятичную систему, и заодно проверим правильность наших вычислений.

Выглядеть это будет следующим образом:

1*23+ 0*22+0*21+1*20= 8+0+0+1 =9.

При изучении данной темы удобно использовать таблицу со степенями двойки. Это существенно уменьшит количество времени, необходимое для проведения вычислений.

История чисел и систем счисления

Непозиционные системы древности

В древние времена, когда люди начали считать, появилась потребность в записи чисел. Первоначально количество предметов отображали равным количеством каких-нибудь значков: насечек, черточек, точек.

Изучение археологами «записок» времен палеолита на кости, камне, дереве показало, что люди стремились группировать отметки по 3, 5, 7, 10 штук. Такая группировка облегчала счет. Люди учились считать не только единицами, но и тройками, пятерками и пр. Поскольку первым вычислительным инструментом у человека были пальцы, поэтому и счет чаще всего вели группами по 5 или по 10 предметов.

В дальнейшем свое название получили десяток десятков (сотня), десяток сотен (тысяча) и т. д. Такие узловые числа для удобства записи стали обозначать особыми значками — цифрами. Если при подсчете предметов их оказывалось 2 сотни, 5 десятков и еще 4 предмета, то при записи этой величины дважды повторяли знак сотни, пять раз — знак десятков и четыре раза знак единицы.

В таких системах счисления от положения знака в записи числа не зависит величина, которую он обозначает; поэтому они называются непозиционными системами счисления.

Непозиционными системами пользовались древние египтяне, греки, римляне и некоторые другие народы древности.

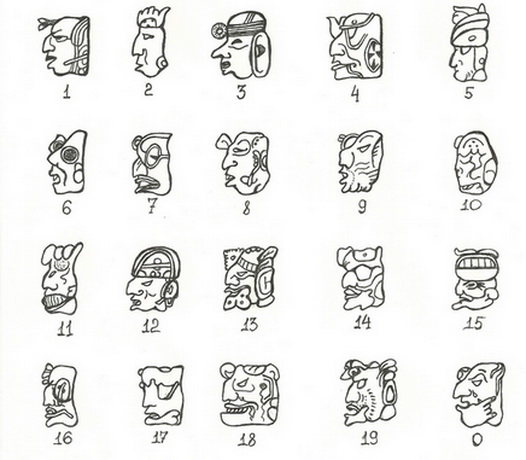
Цифры майя

До нас дошла римская система записи чисел (римские цифры), которая в некоторых случаях применяется в нумерации (века, тома в собрании сочинений, главы книги). В римской системе в качестве цифр используются латинские буквы:

 I V  X   L   С    D     М

1 5 10 50 100 500 1000

На Руси вплоть до XVIII века использовалась непозиционная система славянских цифр. Буквы кириллицы (славянского алфавита) имели цифровое значение, если над ними ставился специальный знак ~ (титло). Например: