Двоичная система знаковая: Двоичная система счисления — Википедия – Дополнительный код — Википедия

Основы двоичной арифметики

1. Сложение: 0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 0 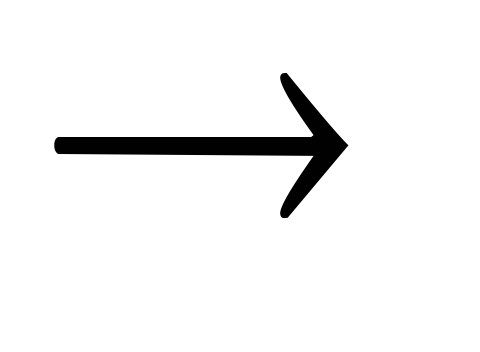1 (перенос в старший разряд)

• Пример сложения многоразрядных чисел. Сложение чисел в двоичной системе счисления.     Запись:         2            10            0000000000000010       +3     +11     + 0000000000000011     5            101          0000000000000101

• Требуется сложить два числа 18₁₀ и 23₁₀

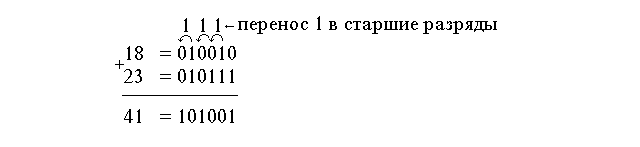
    При сложении чисел надо обязательно проговаривать алгоритм сложения. Следует учитывать, что сложение, как обычно, нужно начинать с младшего разряда. Если сумма единиц разряда окажется равной или большей основания системы счисления, то возникает перенос единицы в старший разряд. После сложения cледует обязательно сделать обратный перевод и убедиться, что число 101 — действительно число 5 в десятичной системе счисления.

2. Вычитание: 0 – 0 = 0

1 – 1 = 0

1 – 0 = 1

0 – 1 = 1 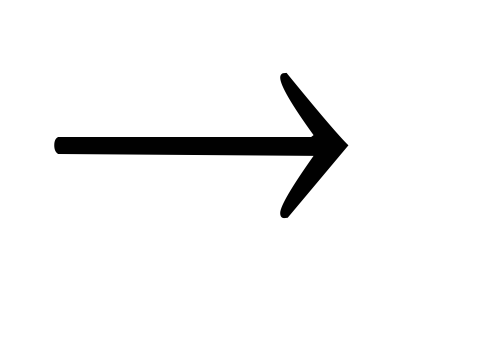заём из старшего разряда

Вычитание двоичных чисел. В компьютере вычитание заменяется сложением с отрицательным числом, представленным в дополнительном коде.     Запись:       14            1110          0000000000001110     

   -9    +1001   +1111111111110111   5            101           10000000000000101

    Так как под целое число отводится 16 разрядов, то старшая единица теряется. Ответ получается 101.

3. Умножение: 0 х 0 = 0

1 х 0 = 0

0 х 1 = 0

1 х 1 = 1

Умножение чисел в двоичной системе счисления.                                         110                                       *101                                           110                                    + 000                                      110                                          11110

Подчеркиваем, что при умножении 1•1 = 1 и 1•0 = 0. Анализируя примеры умножения в двоичной системе счисления, необходимо обратить внимание учащихся на важную особенность выполнения этой операции в данной системе счисления. Так как очередная цифра множителя может быть только 1 или 0, то промежуточное произведение равно либо множимому, либо 0. Таким образом, операция умножения в двоичной системе фактически не производится: в качестве промежуточного произведения записывается либо множимое, либо 0, а затем промежуточные произведения суммируются. Иначе говоря, операция умножения заменяется последовательным сложением.

Двоичные числа со знаком

При выполнении различных операций в современных цифровых устройствах и системах числа обычно представляются в двоичной системе счисления. Это связано с тем, что для представления смысла символов цифр двоичной системы счисления можно использовать простые электронные схемы с двумя электрическими состояниями. Принято, что символ “1” представляется некоторым стандартным уровнем напряжения или тока, а “0” — нулевым или близким к нулю уровнем напряжения или тока.

Арифметические операции над двоичными числами могут производиться по тем же правилам, что и над десятичными, однако, с целью упрощения цифровых систем для выполнения арифметических операций применяют алгоритмы, отличные от алгоритмов действий десятичной арифметики.

В двоичной системе счисления для представления знака числа используется дополнительный знаковый разряд (один или несколько разрядов), который располагается перед старшим числовым разрядом. Для положительных чисел значение знакового разряда Зн.р.=0, для отрицательного числа Зн.р.=1.

Операция вычитания в цифровых системах реализуется с помощью операции сложения. Вычитаемое при этом представляется в дополнительном коде (если расчет не требует высокой точности — в обратном коде).

Двоичный код со знаком называют также прямым кодом. В качестве примера рассмотрим положительное и отрицательное числа, десятичный эквивалент которых равен 46₁₀.

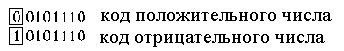
Обратный код получается путем замены всех “0” на “1” и всех “1” на “0” прямого кода (двоичного числа со знаком). Причем, знаковый разряд при этом остается неизменным.

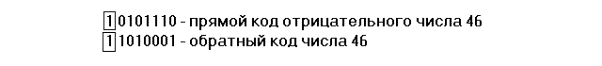
Замена “0” на единицу (“1”) называется инвертированием (также и замена “1” на “0”).

Обратный код, дополненный единицей в младшем разряде, называется дополнительным кодом. Последовательность действий при получении дополнительного кода:

Обратный и дополнительный коды позволяют использовать вместо вычитания операцию сложения, при этом результат автоматически получается нужный.

Десятичное число	Прямой код	Обратный код	Дополнит. код
+7	0111	0111	0111
+6	0110	0110	0110
+5	0101	0101	0101
+4	0100	0100	0100
+3	0011	0011	0011
+2	0010	0010	0010
+1	0001	0001	0001
0	0000	0000	0000
	1000	1111	1111
-1	1001	1110	1111
-2	1010	1101	1110
-3	1011	1100	1101
-4	1100	1011	1100
-5	1101	1010	1011
-6	1110	1001	1010
-7	1111	1000	1001
-8	11000	10111	1000

Двоичная система счисления — это… Что такое Двоичная система счисления?

Системы счисления в культуре
Индо-арабская система счисления
Арабская Индийские Тамильская Бирманская	Кхмерская Лаоская Монгольская Тайская
Восточноазиатские системы счисления
Китайская Японская Сучжоу Корейская	Вьетнамская Счётные палочки
Алфавитные системы счисления
Абджадия Армянская Ариабхата Кириллическая	Греческая Эфиопская Еврейская Катапаяди
Другие системы
Вавилонская Египетская Этрусская Римская	Аттическая Кипу Майская
Позиционные системы счисления
Десятичная система счисления (10)
2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60
Нега-позиционная система счисления
Симметричная система счисления
Смешанные системы счисления
Фибоначчиева система счисления
Непозиционные системы счисления
Единичная (унарная) система счисления
Список систем счисления

Двоичная система счисления — позиционная система счисления с основанием 2.

Двоичные цифры

В этой системе счисления числа записываются с помощью двух символов (0 и 1).

История

• В 1605 году Френсис Бэкон описал систему, буквы алфавита которой могут быть сведены к последовательностям двоичных цифр, которые в свою очередь могут быть закодированы как едва заметные изменения шрифта в любых случайных текстах. Важным шагом в становлении общей теории двоичного кодирования является замечание о том, что указанный метод может быть использован применительно к любым объектам.^[7] (См. Шифр Бэкона)

• Современная двоичная система была полностью описана Лейбницем в XVII веке в работе Explication de l’Arithmétique Binaire^[8]. В системе счисления Лейбница были использованы цифры 0 и 1, как и в современной двоичной системе. Как человек, увлекающийся китайской культурой, Лейбниц знал о книге Перемен и заметил, что гексаграммы соответствуют двоичным числам от 0 до 111111. Он восхищался тем, что это отображение является свидетельством крупных китайских достижений в философской математике того времени.^[9]

• В 1937 году Клод Шеннон представил к защите кандидатскую диссертацию Символический анализ релейных и переключательных схем в MIT, в которой булева алгебра и двоичная арифметика были использованы применительно к электронным реле и переключателям. На диссертации Шеннона по существу основана вся современная цифровая техника.

• В ноябре 1937 года Джордж Штибиц, впоследствии работавший в Bell Labs, создал на базе реле компьютер «Model K» (от англ. «Kitchen», кухня, где производилась сборка), который выполнял двоичное сложение. В конце 1938 года Bell Labs развернула исследовательскую программу во главе со Штибицом. Созданный под его руководством компьютер, завершённый 8 января 1940 года, умел выполнять операции с комплексными числами. Во время демонстрации на конференции American Mathematical Society в Дартмутском колледже 11 сентября 1940 года Штибиц продемонстрировал возможность посылки команд удалённому калькулятору комплексных чисел по телефонной линии с использованием телетайпа. Это была первая попытка использования удалённой вычислительной машины посредством телефонной линии. Среди участников конференции, бывших свидетелями демонстрации, были Джон фон Нейман, Джон Мокли и Норберт Винер, впоследствии писавшие об этом в своих мемуарах.

Запись двоичных чисел

Двоичная система счисления является комбинацией двоичной системы кодирования и показательной весовой функции с основанием равным 2. Положительные целые числа (без знака) записываются в виде:

где:

•  — представляемое число, первый индекс — основание системы кодирования (размерность множества цифр a={0,1}), второй индекс — основание весовой показательной функции b (в двоично-десятичном кодировании b=10),
•  — запись числа, строка цифровых знаков,
•  — обозначение основания системы кодирования и основания системы счисления,
•  — количество цифр (знаков) в числе x_2,2,
•  — порядковый номер цифры,
•  — цифры числа x_2,2 из множества a={0,1}, в двоичной системе счисления основание системы кодирования равно 2,
•  — основание показательной весовой функции, основание системы счисления,
•  — весовая показательная функция, создающая весовые коэффициенты.

Количество записываемых кодов (чисел) зависит от основания системы кодирования — c, определяется в комбинаторике и равно числу размещений с повторениями:

где:

Количество записываемых кодов (чисел) от основания показательной функции — b не зависит.
Основание показательной функции — b определяет диапазон представляемых числами x_2,b величин и разреженность представляемых чисел на числовой оси.

Целые числа являются частными суммами степенного ряда:

в котором коэффициенты a_n берутся из множества R=a{0,1}, X=2, n=k, а верхний предел в частных суммах ограничен с до — n-1.

Целые числа со знаком записываются в виде:

где:

•  — знак числа из множества z={+,-}, у положительных целых чисел знак зачастую опускается.

Дробные числа записываются в виде:

где:

•  — число цифр дробной части числа,
•  — весовые коэффициенты из множества ,
• основание системы кодирования равно 2,
•  — основание показательной весовой функции, основание системы счисления.

Следует отметить, что число может быть записано в двоичном коде, а система счисления при этом может быть не двоичной, а с другим основанием. Пример: двоично-десятичное кодирование, в котором десятичные цифры записываются в двоичном виде, а система счисления — десятичная.

Сложение, вычитание и умножение двоичных чисел

Таблица сложения

Пример сложения «столбиком» (14 + 5 = 19):

		1	↖
+		1	1	1	0
			1	0	1
	1	0	0	1	1

Таблица вычитания

—	0	1
0	0	1
1	(заём из старшего разряда) 1	0

Таблица умножения

Пример умножения «столбиком» (14 × 5 = 70):

×				1	1	1	0
					1	0	1
+				1	1	1	0
		1	1	1	0
	1	0	0	0	1	1	0

Преобразование чисел

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

512

256

128

64

32

16

8

4

2

1

Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1, называется двоичной точкой.

Преобразование двоичных чисел в десятичные

Допустим, вам дано двоичное число 110001. Для перевода в десятичное просто запишите его справа налево как сумму по разрядам следующим образом:

.

Можно записать это в виде таблицы следующим образом:

512	256	128	64	32	16	8	4	2	1
				1	1	0	0	0	1
				+32	+16				+1

Точно так же, начиная с двоичной точки, двигайтесь справа налево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа.
Таким образом, двоичное число 110001 равнозначно десятичному 49.

Преобразование методом Горнера

Для того, чтобы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47. Перевод дробных чисел методом Горнера 1) 0,1101₂=0,X₁₀ (рассматриваем цифры в обратном порядке)
1:2=0,5
0,5+0=0,5
0,5:2=0,25
0,25+1=1,25
1,25:2=0,625
0,625+1=1,625
1,625:2=0,8125
Ответ: 0,1101₂= 0,8125₁₀
2) 0,356₈=0,X₁₀ (рассматриваем цифры в обратном порядке)
6:8=0,75
0,75+5=5,75
5,75:8=0,71875
0,71875+3=3,71875
3,71875:8=0,46484375
Ответ: 0,356₈=0,46484375₁₀
3) 0,A6E₁₆=0,X₁₀ (рассматриваем цифры в обратном порядке)
14:16=0,875
0,875+6=6,875
6,875:16=0,4296875
0,4296875+10=10,4296875
10,4296875:16=0,65185546875
Ответ: 0,A6E₁₆=0,65185546875₁₀

Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

19 /2 = 9  с остатком 1
9  /2 = 4  c остатком 1
4  /2 = 2  без остатка 0
2  /2 = 1  без остатка 0
1  /2 = 0  с остатком 1

Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справа налево. То есть нижнее число будет самым левым и.т.д. В результате получаем число 19 в двоичной записи: 10011.

Преобразование дробных двоичных чисел в десятичные

Нужно перевести число 1011010,101 в десятичную систему. Запишем это число следующим образом:

Или по таблице:

64	32	16	8	4	2	1	0.5	0.25	0.125
1	0	1	1	0	1	0.	.1	0	1
+64		+16	+8		+2		+0.5		+0.125

Преобразование дробных десятичных чисел в двоичные

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

• Вначале переводится целая часть десятичной дроби в двоичную систему счисления;
• Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;
• В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;
• Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206₁₀=11001110₂ по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:
0,116 • 2 = 0,232
0,232 • 2 = 0,464
0,464 • 2 = 0,928
0,928 • 2 = 1,856
0,856 • 2 = 1,712
0,712 • 2 = 1,424
0,424 • 2 = 0,848
0,848 • 2 = 1,696
0,696 • 2 = 1,392
0,392 • 2 = 0,784
и т. д.
Получим: 206,116₁₀=11001110,0001110110₂

Применения

В цифровых устройствах

Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:

• Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток (ток больше пороговой величины) — нет тока (ток меньше пороговой величины), индукция магнитного поля больше пороговой величины или нет (индукция магнитного поля меньше пороговой величины) и т. д.
• Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину напряжения, тока или индукции магнитного поля, потребуется ввести два пороговых значения и два компаратора, что не будет способствовать помехоустойчивости и надёжности хранения информации.^{[источник не указан 770 дней]}
• Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.

В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует (очевидно) один двоичный разряд двоичного регистра, то есть двоичный триггер с двумя состояниями (0,1).

В английской системе мер

При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7¹⁵/₁₆″, 3¹¹/₃₂″ и т. д.

Интересные факты

См. также

Примеры чисел-степеней двойки

Степень	Значение
0	1
1	2
2	4
3	8
4	16
5	32
6	64
7	128
8	256
9	512
10	1024
11	2048
12	4096
13	8192
14	16384
15	32768
16	65536
17	131072
18	262144
19	524288
20	1048576
21	2097152
22	4194304
23	8388608
24	16777216
25	33554432
26	67108864
27	134217728
28	268435456
29	536870912
30	1073741824
31	2147483648
32	4294967296
33	8589934592
34	17179869184
35	34359738368
36	68719476736
37	137438953472
38	274877906944
39	549755813888
40	1099511627776
41	2199023255552
42	4398046511104
43	8796093022208
44	17592186044416
45	35184372088832
46	70368744177664
47	140737488355328
48	281474976710656
49	562949953421312
50	1125899906842624
51	2251799813685248

Примечания

1. ↑ Sanchez, Julio & Canton, Maria P. (2007), «Microcontroller programming: the microchip PIC», Boca Raton, Florida: CRC Press, с. 37, ISBN 0-8493-7189-9 
2. ↑ W. S. Anglin and J. Lambek, The Heritage of Thales, Springer, 1995, ISBN 0-387-94544-X
3. ↑ Ordish George, Hyams, Edward. The last of the Incas: the rise and fall of an American empire. — New York: Barnes & Noble, 1996. — С. 80. — ISBN 0-88029-595-3
4. ↑ Experts ‘decipher’ Inca strings. Архивировано из первоисточника 18 августа 2011.
5. ↑ Carlos Radicati di Primeglio, Gary Urton Estudios sobre los quipus. — P. 49.
6. ↑ Dale Buckmaster (1974). «The Incan Quipu and the Jacobsen Hypothesis». Journal of Accounting Research 12 (1): 178-181. Проверено 2009-12-24.
7. ↑ Bacon, Francis, «The Advancement of Learning», vol. 6, London, сс. Chapter 1, <http://home.hiwaay.net/~paul/bacon/advancement/book6ch2.html> 
8. ↑ http://www.leibniz-translations.com/binary.htm Leibniz Translation.com EXPLANATION OF BINARY ARITHMETIC
9. ↑ Aiton, Eric J. (1985), «Leibniz: A Biography», Taylor & Francis, сс. 245–8, ISBN 0-85274-470-6 

Ссылки

Обсуждение:Двоичная система счисления — Википедия

Уважаемые «викиавторы» (не знаю как к вам обратиться :)) В статье не раскрыт маленький, но очень спорный вопрос — как правильно читать числа в двоичной записи. к примеру: 11₂ — следует считать как «три» или как «одиннадцать»? для меня это казалось очевидным, до тех пор, пока я не встретил противоположную точку зрения. Изученная литература также не дала ответа, в математической литературе не встречаются числа прописью. 188.92.110.27 09:07, 17 сентября 2012 (UTC)CTPAHHuK

• Вопрос интересный. Я не встречал таких правил, но я бы произносил по символам «один-один». Так например число записанное с шеснадцатиричным основание 1B3F по другому прочитать просто нельзя. —Pintg 08:33, 18 сентября 2012 (UTC)

Отрицательные числа вообще нераскрыты 217.151.131.30 07:13, 30 июня 2010 (UTC)

В двоичной системе же нельзя чтобы первая была 0!Но так получается если переводить чётное по примеру в вики:

18|0

9 |1

4 |0

2 |0

Замечание не верно даже на половину ;-).Произведенные вычисления не верны. По примеру следует так:

18/2=9 | 0
 9/2=4 | 1
 4/2=2 | 0
 2/2=1 | 0
 1/2=0 | 1
 Полученное таким образом двоичное число 10010 легко переводится в десятичное 18.
Утверждать что:"В двоичной системе же нельзя чтобы первая была 0!" - вообще кощунство!!! :-D 
 То есть: начинаем счет с "0" - записывается в двоичном формате как "0" или "000000",
причем нолей ставте сколько  необходимо, в переводе на десятичный формат все равно будет "0".
Так же запись в двоичном формате единицы выглядит как "01"  или "000000001".
Даже число "18" можно в двоичной системе записать как "10010" и как "0010010" 
  Все верно! 95.28.19.149 06:27, 24 октября 2009 (UTC)Oll

Вопросы и пожелания пишите сюда.

«Двоичная система счисления (или система счисления с основанием 2) — это положительная целочисленная позиционная (поместная) система счисления, позволяющая представить различные численные значения с помощью двух символов. Чаще всего это 0 и 1.» ограничения «положительная», «целочисленная» — лишние. Никто не запрещает поставить ни запятую, ни знак «-» перед числом. 79.98.53.214 20:17, 12 января 2009 (UTC)

«Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину индукции магнитного поля, потребуется ввести два пороговых значения, что не будет способствовать помехоустойчивости и надёжности хранения информации.» ещё раз «что не будет способствовать помехоустойчивости и надёжности хранения информации.»

-)))

«и тем быстрее он может работать» очень спорно 79.98.53.214 20:50, 12 января 2009 (UTC)
Спорно — для тех, кто не понял, для тех, кто понял — бесспорно.92.243.182.100 21:51, 4 января 2011 (UTC)

Как двоичные в десятичные переводить с помошью таблицы понятно а вот «наоборот» табличным способом, что то я не разобрался!

94.253.45.207 13:56, 5 апреля 2009 (UTC)

Предлагается дату 10.10.10 (в полном формате — «10.10.10 10:10:10») сделать датой (днём) двоичной системы счисления Fractaler 14:17, 10 сентября 2009 (UTC)

Сравнение с другими системами счисления[править код]

Сравнение с другими системами счисления имеет смысл только в контексте применения двоичной системы счисления в цифровых устройствах. Именно поэтому информация перенесена в раздел Применения -> В цифровых устройствах. Maxal 19:08, 3 ноября 2009 (UTC)

А как называется система: 1-цифра, отвечает есть ли там 1 2-есть ли там 2 3-есть ли там 4 и т.д.

к примеру: 0001 — 8 1010 — 5 1000 — 1 00001-16 — Эта неподписанная реплика была добавлена участником 14:01, 6 марта 2010 (обс. · вклад) в 95.190.58.127 (UTC). Подписывайте свои сообщения с помощью ~~~~.

Та же двоичная, но задом наперёд? Разве это где-нибудь употребляется? infovarius 19:51, 6 марта 2010 (UTC)

При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″

Это что за бред? Какое отношение имеет обыкновенная дробь к двоиным числам? 91.151.37.213 11:53, 27 февраля 2011 (UTC)

Это двоичная дробь — т.е. дробь, знаменатель которой является степенью двойки. Даже если она записана как обычная, она всё равно остаётся двоичной. — Monedula 18:57, 27 февраля 2011 (UTC)

Парадокс? или Я где-то ошибся?[править код]

Расчитывая «простейшие» расчеты в двоичной системе «нашел» парадокс.
Перевожу 5₁₀ в двоичною.

[5\2=2] 1
[2\2=1] 0
[1\2=0] 1

5₁₀=101₂
Так-же перевел 2 и 3 из десятичной в двоичною.

210=102
310=112

Добавим 11₂ и 10₂.

 1 
10
+11
101

Пока что всё правильно:2+3=5.
Дальше 101₂-11₂.

1   
101
-11
000

СТОП. 5-3=0? Ну ладно пусть 101₂-10₂.

1  
101
-10
001

Да ладно, вы серьзно думаете что 5-3=0 и 5-2=1? Найдите в расчетах ошибку, а то кажеться полный бред здесь. 93.75.45.28 13:33, 12 апреля 2014 (UTC)

• Вычитание в столбик как делается забыли?

1   
101
-11
010

ASDFS 15:35, 12 апреля 2014 (UTC)

Хорошо, может быть человек где-то ошибся, но програмы расчёта!!! Например здесь: http://math.semestr.ru/inf/operation.php
Подставим 101-11 и 101-10(поставить вычитание и двоичную систему, изначально цифры подаються в 10-чной) и получим по нулю и единице! То есть и компьютеры и люди ошиблись? 93.75.45.28 21:51, 12 апреля 2014 (UTC)

• Это все последствия краха школьного образования. Если программист необразован то компьютер не виноват. Заканчивайте этот балаган, а то мне кажется что вы это затеяли чтобы ссылку прилепить. ASDFS 22:26, 12 апреля 2014 (UTC)

Почему двоичное кодирование является универсальным? Методы программирования

Компьютер обрабатывает большое количество информации. Аудиофайлы, картинки, тексты – все это необходимо воспроизвести или вывести на экран. Почему двоичное кодирование является универсальным методом программирования информации любого технического оборудования?

Чем отличается кодирование от шифрования?

Зачастую люди отождествляют понятия «кодирование» и «шифрование», когда на самом деле они имеют разный смысл. Так, шифрованием называют процесс преобразования информации с целью ее сокрытия. Расшифровать зачастую может сам человек, который изменил текст, или специально обученные люди. Кодирование же применяется для обработки информации и упрощения работы с ней. Обычно используется общая таблица кодировки, знакомая всем. Она же встроена в компьютер.

Принцип двоичного кодирования

Двоичное кодирование основывается на использовании всего лишь двух символов — 0 и 1 — для обработки информации, используемой различными устройствами. Эти знаки назвали двоичными цифрами, на английском – binary digit, или bit. Каждый из символов двоичного кода занимает память компьютера в 1 бит. Почему двоичное кодирование является универсальным методом обработки информации? Дело в том, что компьютеру легче обрабатывать меньшее количество символов. От этого напрямую зависит и продуктивность работы ПК: чем меньше функциональных задач нужно выполнить устройству, тем выше скорость и качество работы.

Принцип двоичного кодирования встречается не только в программировании. С помощью чередования глухих и звонких ударов барабана жители Полинезии передавали информацию друг другу. Сходный принцип применяется и в азбуке Морзе, где для передачи сообщения используются длинные и короткие звуки. «Телеграфная азбука» используется и сегодня.

Где используется двоичное кодирование?

Двоичное кодирование информации в компьютере используется повсеместно. Каждый файл, будь то музыка или текст, должен быть запрограммирован, чтобы в последующем он мог быть легко обработан и прочитан. Система двоичного кодирования полезна для работы с символами и числами, аудиофайлами, графикой.

Двоичное кодирование чисел

Сейчас в компьютерах числа представлены в закодированном виде, непонятном для обычного человека. Использование арабских цифр так, как мы себе представляем, для техники нерационально. Причиной тому является необходимость присваивать каждому числу свою неповторимый символ, что сделать порой невозможно.

Существуют две системы счисления: позиционная и непозиционная. Непозиционная система основана на использовании латинских букв и знакома нам в виде греческих цифр. Такой способ записи достаточно сложен для понимания, поэтому от него отказались.

Позиционная система счисления используется и сегодня. Сюда входит двоичное, десятичное, восьмеричное и даже шестнадцатеричное кодирование информации.

Десятичной системой кодирования мы пользуемся в быту. Это привычные для нас арабские цифры, которые понятны каждому человеку. Двоичное кодирование чисел отличается использованием только нуля и единицы.

Целые числа переводятся в двоичную систему кодирования путем деления их на 2. Полученные частные также поэтапно делятся на 2, пока не получится в итоге 0 или 1. Например, число 123₁₀ в двоичной системе может быть представлено в виде 1111011₂. А число 20₁₀ будет выглядеть как 10100₂.

Индексы 10 и 2 обозначаются, соответственно, десятичную и двоичную систему кодирования чисел. Символ двоичного кодирования используется для упрощения работы со значениями, представленными в разных системах счисления.

Методы программирования десятичных чисел основаны на “плавающей запятой”. Для того чтобы правильно перевести значение из десятичной в двоичную систему кодирования, используют формулу N = M х qp. М – это мантисса (выражение числа без какого-либо порядка), p – это порядок значения N, а q – основание системы кодирование (в нашем случае 2).

Не все числа являются положительными. Для того чтобы различить положительные и отрицательные числа, компьютер оставляет место в 1 бит для кодирования знака. Здесь ноль представляет знак плюс, а единица – минус.

Использование такой системы счисления упрощает для компьютера работу с числами. Вот почему двоичное кодирование является универсальным при вычислительных процессах.

Двоичное кодирование текстовой информации

Каждый символ алфавита кодируется своим набором нулей и единиц. Текст состоит из разных символов: букв (прописных и строчных), арифметических знаков и других различных значений. Кодирование текстовой информации требует использования 8 последовательных двоичных значений от 00000000 до 11111111. Таким образом можно преобразовать 256 различных символов.

Чтобы не было путаницы в кодировании текста, используются специальных таблицы значений для каждого символа. В них присутствует латинский алфавит, арифметические знаки и знаки особого назначения (например, €, ¥, © и другие). Символы промежутка 128-255 кодируют национальный алфавит страны.

Для кодирования 1 символа требуется 8 бит памяти. Для упрощения подстчетов 8 бит приравниваются к 1 байту, поэтому общее место на диске для текстовой информации измеряется в байтах.

Большинство персональных компьютеров оснащены стандартной таблицей кодировки ASCII (American Standard Code for Information Interchange). Также используются другие таблицы, в которых система кодирования текстовой информации отличается. К примеру, первая известная кодировка символов называется КОИ-8 (код обмена информацией 8-битный), и работает она на компьютерах с ОС UNIX. Также широко встречается таблица кодов СР1251, которая была создана для операционной системы Windows.

Двоичное кодирование звуков

Еще одна причина, почему двоичное кодирование является универсальным методом программирования информации, — это его простота при работе с аудиофайлами. Любая музыка представляет собой звуковые волны разной амплитуды и частоты колебания. От этих параметров зависит громкость звука и его высота тона.

Чтобы запрограммировать звуковую волну, компьютер делит ее условно на несколько частей, или «выборок». Число таких выборок может быть большим, поэтому существует 65536 различных комбинаций нулей и единиц. Соответственно, современные компьютеры оснащены 16-битными звуковыми картами, что означает использование 16 двоичных цифр для кодирования одной выборки звуковой волны.

Чтобы воспроизвести аудиофайл, компьютер обрабатывает запрограммированные последовательности двоичного кода и соединяет их в одну непрерывную волну.

Кодирование графики

Графическая информация может быть представлена в виде рисунков, схем, картинок или слайдов в PowerPoint. Любая картинка состоит из мелких точек – пикселей, которые могут быть окрашены в разный цвет. Цвет каждого пикселя кодируется и сохраняется, и в итоге мы получаем полноценное изображение.

Если картинка черно-белая, код каждого пикселя может быть либо единицей, либо нулем. Если используется 4 цвета, то код каждого из них состоит из двух цифр: 00, 01, 10 или 11. По этому принципу различают качество обработки любого изображения. Увеличение или уменьшение яркости также влияет на количество используемых цветов. В лучшем случае компьютер различает около 16 777 216 оттенков.

Заключение

Существуют разные методы программирования информации, среди которых двоичное кодирование является наиболее эффективным. Всего лишь с помощью двух символов — 1 и 0 — компьютер легко прочитывает большинство файлов. При этом скорость обработки намного выше, нежели использовалась бы, например, десятичная система программирования. Простота этого метода делает его незаменимым для любой техники. Вот почему двоичное кодирование является универсальным среди своих аналогов.

Лекция на тему «Машинные коды двоичного числа»

Машинные коды двоичного числа

В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. При помощи этих кодов упрощается определение знака результата операции. Операция вычитания (или алгебраического сложения) чисел сводится к арифметическому сложению кодов, облегчается выработка признаков переполнения разрядной сетки. В результате упрощаются устройства ЭВМ, выполняющие арифметические операции.

Для представления чисел со знаком в ЭВМ применяют прямой, обратный и дополнительный коды.

Общая идея построения кодов такова. Код трактуется как число без знака, а диапазон представляемых кодами чисел без знака разбивается на два поддиапазона. Один из них представляет положительные числа, другой – отрицательные. Разбиение выполняется таким образом, чтобы принадлежность к поддиапазону определялась максимально просто.

Наиболее распространенным и удобным является формирование кодов таким образом, чтобы значение старшего разряда указывало на знак представляемых чисел, т.е. использование такого кодирования позволяет говорить о старшем разряде как о знаковом (бит знака) и об остальных как о цифровых разрядах кода.

Прямой код

Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.

Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:

        0 0001101–положительное число                                                   1 0001101 – отрицательное число

Количество значений, которые можно поместить в семиразрядной ячейке со знаком в дополнительном разряде равно 256. Это совпадает с количеством значений, которые можно поместить в восьмиразрядную ячейку без указания знака. Однако диапазон значений уже другой, ему принадлежат значения от -128 до 127 включительно (при переводе в десятичную систему счисления).

При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.

Обратный код

В обратном коде (ОК), также как и в прямом коде, для обозначения знака положительного числа используется бит, равный нулю, и знака отрицательного – единице.

Обратный код положительного двоичного числа совпадает с его прямым кодом. Обратный код отрицательного двоичного числа содержит единицу в знаковом разряде, формируется дополнением модуля исходного числа нулями до самого старшего разряда модуля, а затем поразрядной заменой всех нулей числа на единицу и всех единиц на нули. Обратный перевод осуществляется в той же последовательности.

 

 

 

 

 

 

Пример. Записать обратный код чисел  и 

Решение:

                                  

                                                               

Работа с обратным кодом вызывает ряд трудностей. В частности, возникают два нуля: положительный и отрицательный, т.е. в прямом коде (в котором представлены положительные числа) имеет место , а в обратном коде (в котором представлены отрицательные числа) .

Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.

Дополнительный код

В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой код используется для представления положительных чисел, а дополнительный – для представления отрицательных. Поэтому, если в первом разряде находится 1, то мы имеем дело с дополнительным кодом и с отрицательным числом.

Все остальные разряды числа в дополнительном коде сначала инвертируются, т.е. заменяются противоположными (0 на 1, а 1 на 0). Например, если 1 0001100 – это прямой код числа, то при формировании его дополнительного кода, сначала надо заменить нули на единицы, а единицы на нули, кроме первого разряда. Получаем 1 1110011. Но это еще не окончательный вид дополнительного кода числа.

Далее следует прибавить единицу к получившемуся инверсией числу:

1 1110011 + 1 = 1 1110100

В итоге и получается число, которое принято называть дополнительным кодом числа.

Причина, по которой используется дополнительный код числа для представления отрицательных чисел, связана с тем, что так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.

 

 

Операция сложения положительного числа и отрицательного числа, представленного в прямом коде

1. Прямой код числа 5: 0 000 0101
   Прямой код числа -7: 1 000 0111
2. Два исходных числа сравниваются. В разряд знака результата записывается знак большего исходного числа.
3. Если числа имеют разные знаки, то вместо операции сложения используется операция вычитания из большего по модулю значения меньшего. При этом первый (знаковый) разряд в операции не участвует.
4. _ 000 0111
5.   000 0101
6. ————-
7.   000 0010
8. После выполнения операции учитывается первый разряд. Результат операции 1 000 0010, или -2₁₀.

Операция сложения положительного числа и отрицательного числа, представленного в дополнительном коде

1. Прямой код числа 5: 0 000 0101
   Прямой код числа -7: 1 000 0111
2. Формирование дополнительного кода числа -7.
   Прямой код : 1 000 0111
   Инверсия : 1 111 1000
   Добавление единицы: 1 111 1001
3. Операция сложения.
4.   0 000 0101
5. + 1 111 1001
6.   —————
7.   1 111 1110
8. Проверка результата путем преобразования к прямому коду.
   Дополнительный код: 1 111 1110
   Вычитание единицы : 1 111 1101
   Инверсия : 1 000 0010 (или -2₁₀)

 

Двоично-десятичный код — Википедия

Материал из Википедии — свободной энциклопедии

Перевод десятичных цифр в двоично-десятичный код

Двоично-десятичный код (англ. binary-coded decimal), BCD, 8421-BCD  — форма записи рациональных чисел, когда каждый десятичный разряд числа записывается в виде его четырёхбитного двоичного кода.

Например, десятичное число 311₁₀ будет записано в двоичной системе счисления в двоичном коде как 1 0011 0111₂, а в двоично-десятичном коде как 0011 0001 0001_BCD.

При помощи 4 бит можно закодировать 16 цифр. Из них используются 10. Остальные 6 комбинаций в двоично-десятичном коде являются запрещёнными. Таблица соответствия двоично-десятичного кода и десятичных цифр:

Двоично-десятичный код также применяется в телефонной связи. В этом случае кроме десятичных цифр кодируются символы ‘*’ или ‘#’, или любые другие. Для записи этих символов в двоично-десятичном коде используются запрещенные комбинации:

Преимущества[править | править код]

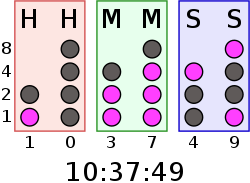Часы с двоично-десятичной системой индикации. В этих часах каждая колонка отображает десятичное число в двоично-десятичной системе.

• Упрощён вывод чисел на индикацию — вместо последовательного деления на 10 требуется просто вывести на индикацию каждый полубайт. Аналогично, проще ввод данных с цифровой клавиатуры.
• Для дробных чисел (как с фиксированной, так и с плавающей запятой) при переводе в человекочитаемый десятичный формат и наоборот не теряется точность.
• Упрощены умножение и деление на 10, а также округление.

По этим причинам двоично-десятичный формат применяется в калькуляторах — калькулятор в простейших арифметических операциях должен выводить в точности такой же результат, какой подсчитает человек на бумаге.

Недостатки[править | править код]

• Требует больше памяти.
• Усложнены арифметические операции. Так как в 8421-BCD используются только 10 возможных комбинаций 4-битового поля вместо 16, существуют запрещённые комбинации битов: 1010(10₁₀), 1011(11₁₀), 1100(12₁₀), 1101(13₁₀), 1110(14₁₀) и 1111(15₁₀).

Поэтому, при сложении и вычитании чисел формата 8421-BCD действуют следующие правила:

1. При сложении двоично-десятичных чисел каждый раз, когда происходит перенос бита в старший полубайт, необходимо к полубайту, от которого произошёл перенос, добавить корректирующее значение 0110 (= 6₁₀ = 16₁₀ — 10₁₀: разница количеств комбинаций полубайта и используемых значений).
2. При сложении двоично-десятичных чисел каждый раз, когда встречается недопустимая для полубайта комбинация (число, большее 9), необходимо к каждой недопустимой комбинации добавить корректирующее значение 0110 с разрешением переноса в старшие полубайты.
3. При вычитании двоично-десятичных чисел, для каждого полубайта, получившего заём из старшего полубайта, необходимо провести коррекцию, отняв значение 0110.

Пример операции сложения двоично-десятичных чисел:

Требуется: Найти число A = D + C, где D = 3927, C = 4856

Решение: Представим числа D и C в двоично-десятичной форме:
D = 3927₁₀ = 0011 1001 0010 0111_BCD
C = 4856₁₀ = 0100 1000 0101 0110_BCD

Суммируем числа D и С по правилам двоичной арифметики:

       *         ** 
  0011 1001 0010 0111
+ 0100 1000 0101 0110
  ___________________
= 1000 0001 0111 1101 - Двоичная сумма
+      0110      0110 - Коррекция
  ___________________
  1000 0111 1000 0011

‘*’ — тетрада, из которой был перенос в старшую тетраду

‘**’ — тетрада с запрещённой комбинацией битов

В тетраду, помеченную символом *, добавляем шестёрку, так как по правилам двоичной арифметики перенос унёс с собой 16, а по правилам десятичной арифметики должен был унести 10. В тетраду, помеченную символом **, добавляем шестёрку и разрешаем распространение переноса, так как комбинация битов 1101 (что соответствует десятичному числу 13) является запрещённой.

В системе кодирования «2 из 5»^[en] одна десятичная цифра кодируется 5 битами, из которых 2 бита установлены в 1, а 3 бита — в 0, что даёт ровно 10 комбинаций. Такая система обеспечивает лучшее обнаружение ошибок, поскольку изменение одного бита всегда даст недопустимую комбинацию; также всегда обнаруживаются однонаправленные изменения (несколько изменений 0→1 или 1→0). Кодирование «2 из 5» использовалось в компьютерах серий IBM 7070, IBM 7072 и IBM 7074; также применяется в некоторых странах для маркирования почты штрих-кодом.

Уплотнённые десятичные числа^[en] позволяют разместить 3 десятичные цифры в 10 битах (2¹⁰=1024 комбинации, что достаточно для 3 десятичных цифр), причём кодирование устроено так, что преобразование между 10-битным кодом и тремя отдельными десятичными цифрами можно осуществить с помощью простой и быстрой логической схемы. Такое кодирование используется в десятичных числах с плавающей запятой, описанных в стандарте IEEE 754-2008.

Бинарные числа: двоичная система счисления

Бинарные числа — это числа из двоичной системы счисления, имеющей основание 2. Она непосредственно реализована в цифровой электронике, используется в большинстве современных вычислительных устройств, включая компьютеры, мобильные телефоны и разного рода датчики. Можно сказать, что все технологии нашего времени построены на бинарных числах.

Запись чисел

Любое число, сколь бы большим оно ни было, в двоичной системе записывается посредством двух символов: 0 и 1. Например цифра 5 из всем знакомой десятичной системы в двоичной будет представлено как 101. Бинарные числа могут быть обозначены префиксом 0b или амперсандом (&), например: &101.
Во всех системах счисления, исключая десятичную, символы читаются по одиночке, то есть взятое в пример 101 читается как «один ноль один».

Перевод из одной системы в другую

Программисты, постоянно работающие с двоичной системой счисления, на ходу могут перевести бинарное число в десятичное. Это действительно можно сделать и без всяких формул, особенно если человек имеет представление о том, как работает самая малая часть компьютерного «мозга» — бит.

Цифра ноль так же обозначает 0, а цифра один в двоичной системе тоже будет единицей, но что делать дальше, когда цифры закончились? Десятичная система «предложила» бы в таком случае ввести термин «десяток», а в бинарной системе это будет называться «двойка».

Если 0 это &0 (амперсанд — обозначение двоичной системы), 1 = &1, то 2 будет обозначаться как &10. Тройку тоже можно записать в двух разрядах, она будет иметь вид &11, то есть одна двойка и одна единица. Возможные комбинации исчерпаны, и в десятичной системе на этом этапе вводятся сотни, а в двоичной — «четверки». Четыре — это &100, пять — &101, шесть — &110, семь — &111. Следующая, более крупная единица счета — это восьмерка.

Можно заметить особенность: если в десятичной системе разряды умножаются на десять (1, 10, 100, 1000 и так далее), то в двоичной, соответственно, на два: 2, 4, 8, 16, 32. Это соответствует размеру флеш-карт и прочих накопителей, использующихся в компьютерах и других устройствах.

Что такое бинарный код

Числа, представленные в двоичной системе счисления, называются бинарными, однако в таком виде можно представить и не числовые значения (буквы и символы). Таким образом, в цифрах можно закодировать слова и тексты, правда вид они будут иметь не столь лаконичный, ведь для записи всего одной буквы потребуется несколько нолей и единиц.

Но каким образом компьютерам удается считывать такое количество информации? На самом деле все проще, чем кажется. Люди, привыкшие к десятичной системе счисления, сначала переводят двоичные числа в более привычные, и только потом производят с ними какие-либо манипуляции, а в основе компьютерной логики изначально лежит бинарная система чисел. Единице в технике соответствует высокое напряжение, а нулю — низкое, либо для единицы напряжение есть, а для ноля вообще отсутствует.

Бинарные числа в культуре

Ошибкой будет считать, что двоичная система счисления — это заслуга современных математиков. Хотя бинарные числа и являются основополагающими в технологиях нашего времени, использовались они уже очень давно, причем в разных уголках планеты. Используются длинная линия (единица) и прерывистая (ноль), кодирующие восемь символов, означающих восемь стихий: небо, землю, гром, воду, горы, ветер, огонь и водоем (массу воды). Этот аналог 3-битных цифр описывался в классическом тексте книги Перемен. Триграммы составляли 64 гексаграммы (6-битные цифры), порядок которых в книге Перемен был расположен в соответствии с двоичными цифрами от 0 до 63.

Этот порядок был составлен в одиннадцатом веке китайским ученым Шао Юном, хотя нет доказательств того, что он действительно понимал двоичную систему счисления в целом.

В Индии еще до нашей эры тоже применялись бинарные числа в математической основе для описания поэзии, составленные математиком Пингалой.

Узелковая письменность инков (кипу) считается прообразом современных баз данных. Именно они впервые применили не только бинарный код числа, но и не числовые записи в двоичной системе. Узелковое письмо кипу характерно не только первичными и дополнительными ключами, но и использованием позиционных чисел, кодированием с помощью цвета и сериями повторений данных (циклами). Инки впервые применили способ ведения бухгалтерского учета, называемый двойной записью.

Первый из программистов

Двоичную систему счисления, основанную на цифрах 0 и 1, описал и знаменитый ученый, физик и математик, Готфрид Вильгельм Лейбниц. Он увлекался древней китайской культурой и, изучая традиционные тексты книги Перемен, заметил соответствие гексаграмм бинарным числам от 0 до 111111. Он восхитился свидетельствам подобных достижений в философии и математике для того времени. Лейбница можно назвать первым из программистов и информационных теоретиков. Именно он обнаружил, что если записать группы двоичных чисел вертикально (одно под другим), то в получившихся вертикальных столбцах чисел будут регулярно повторяться ноли и единицы. Это позвонило ему предположить, что возможно существование совершенно новых математических законов.

Лейбниц понял и то, что бинарные числа оптимальны для применения в механике, основой которой должна быть смена пассивных и активных циклов. На дворе был 17 век, а этот великий ученый изобрел на бумаге вычислительную машину, работавшую на основе его новых открытий, однако быстро понял, что цивилизация еще не достигла такого технологического развития, и в его время создание такой машины будет невозможным.