Двоичная система счисления
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов: 0 и 1. Двоичную цифру называют битом. Двоичная система счисления является основной системой представления информации в памяти компьютера.
Сложение, вычитание и умножение двоичных чисел.
Таблица сложения
Пример: 1001 + 10 = 1011
Таблица вычитания
Пример: 1111101 — 10001 = 1101100
Таблица умножения
Пример: 1111 · 1001 = 10000111
Перевод чисел.
Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного.
Пример: 7310 = 10010012
Для перевода двоичного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания двоичной системы счисления на соответствующие цифры в разрядах двоичного числа.
Пример: требуется перевести двоичное число 10110110 в десятичное. В этом числе 8 цифр и 8 разрядов ( разряды считаются, начиная с нулевого, которому соответствует младший бит). Представим его в виде суммы степеней с основанием 2: 101101102 = (1·27)+(0·26)+(1·25)+(1·24)+(0·23)+(1·22)+(1·21)+(0·20) = 128+32+16+4+2 = 18210
Другие заметки по информатике
Двоичная система счисления
☰
В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.
В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную
Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:
1476 = 1000 + 400 + 70 + 6
Можно пойти еще дальше и разложить так:
1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100
Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:
10001001 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*2 2 + 0*21 + 1*20
Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:
1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
100010012 = 13710
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное
Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
двоичная, восьмеричная, шестнадцатеричная — урок. Информатика, 8 класс.
Для кодирования информации в компьютере вместо привычной десятичной системы счисления используется двоичная система счисления.
Двоичной системой счисления люди начали пользоваться очень давно. Древние племена Австралии и островов Полинезии использовали эту систему в быту. Так, полинезийцы передавали необходимую информацию, выполняя два вида ударов по барабану: звонкий и глухой. Это было примитивное представление двоичной системы счисления.
Двоичной системой счисления называется позиционная система счисления с основанием \(2\).
Для записи чисел в ней использовали только две цифры: \(0\) и \(1\).
Для обозначения системы счисления, в которой представляется число, используют нижний индекс, указывающий основание системы. Например, 110112 — число в двоичной системе счисления.
Цифры в двоичном числе являются коэффициентами его представления в виде суммы степеней с основанием \(2\), например:
1012=1 ·22+0 ·21+1 ·20.
В десятичной системе счисления это число будет выглядеть так:
1012=4+0+1=5.
Для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на \(2\) до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример:
Переведём десятичное число \(13\) в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:
Получили 1310=11012.
Пример:
Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:
\(224\) | \(112\) | \(56\) | \(28\) | \(14\) | \(7\) | \(3\) | \(1\) |
\(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(1\) | \(1\) | \(1\) |
22410=111000002.
Восьмеричной системой счисления называется позиционная система счисления с основанием \(8\).
Для записи чисел в восьмеричной системе счисления используются цифры: \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\).
Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в восьмеричной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример:
Переведём восьмеричное число 154368 в десятичную систему счисления.
154368=1 ·84+5 ·83+4 ·82+3 ·81+6 ·80=694210
Пример:
Переведём десятичное число \(94\) в восьмеричную систему счисления.
9410=1368
Шестнадцатеричной системой счисления называется позиционная система счисления с основанием \(16\).
Для записи чисел в шестнадцатеричной системе счисления используются цифры: \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\) и латинские буквы A, B, C, D, E, F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510.
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Для перевода целого десятичного числа в шестнадцатеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на \(16\) до тех пор, пока не получим частное, равное нулю. Исходное число в системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример:
Переведём шестнадцатеричное число \(2\)\(A7\) в десятичное. В соответствии с вышеуказанными правилом представим его в виде суммы степеней с основанием \(16\):
2A716=2 ·162+10 ·161+7 ·160=512+160+7=679.
Пример:
Переведём десятичное число \(158\) в шестнадцатеричную систему счисления.
15810=9E16.
Для перевода числа из любой позиционной системы счисления в десятичную необходима использовать развернутую формулу числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами.
Для перевода целых чисел десятичной системы счисления в число любой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы счисление, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.
Двоичная система счисления — Знаешь как
Содержание статьи
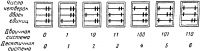При вычислениях мы обычно пользуемся десятичной позиционной системой. В этой системе знаки 0, 1,2, 3, 4, 5, 6, 7, 8, 9, называемые цифрами, представляют нуль и первые девять целых чисел. Десять обозначается двумя цифрами 1 и 0 и является основанием системы. Каждая цифра представленного ряда имеет различную значимость в зависимости от ее позиции или места в числе. Например, в числе 345,2: справа от запятой, две десятых — 2•10-1; слева от запятой — пять единиц — 5-10°; четыре десятка — 4 • 101 и три сотни — 3 • 102. Следовательно, все число представляется так:345,2 = 3 • 102 + 4 • 101 + 5 • 100 + 2 • 10-1 единиц.
Рис. 16-10. Двоичное счисление при работе на конторских счетах
Если представить себе счетчик любой системы, то он в каждом разряде должен быть способным принимать девять различных устойчивых положений. Для ЦВУ оказалась удобной система с основанием 2, называемая двоичной, при которой имеются только две цифры 0 и 1. Когда в первом (правом) разряде вместо единицы должно появиться два (2), то двойка переносится в виде единицы (1) в старший разряд, а в младшем ставится
Такой счет получается, если пользоваться счетами, имеющими на каждой спице только по две костяшки (рис. 16-10).
Ниже приведены несколько чисел, написанных в двоичной системе:
| 1 | — один | 1011 | — одиннадцать |
| 10 | — два | 1100 | — двенадцать |
| 11 | — три | 1101 | — тринадцать |
| 100 | — четыре | 1110 | — четырнадцать |
| 101 | — пять | 1111 | — пятнадцать |
| 110 | — шесть | 10000 | — шестнадцать |
| 111 | — семь | 0,1 | — половина |
| 1000 | — восемь | 0,01 | — четверть |
| 1001 | — девять | 0,001 | — восьмая |
| 1010 | — десять | 0,11 | — три четверти |
Таким образом, число двоичной системы 1011,1 представляет: справа от запятой, одна половина— 1•2-1 и слева от запятой одна единица — 1-20, одна двойка — 1•21, нуль четверок — 0•22 и одна восьмерка—1•23, т. е. (1011,1)2 = 1•23+0•22+1•21+1•20+1•2-1= (8 + 0 + 2 + 1 + 0,5= 11,5)10. Индексы 2 и 10 обозначают основание системы.
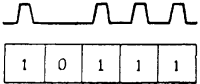Как можно видеть, в этом случае наличие цифры в каждом разряде (1) или отсутствие ее (0) может характеризоваться счетчиками релейного типа, управляемыми импульсами: включено — выключено,есть сигнал напряжения — нет сигнала, намагничен участок магнитной ленты — не намагничен и т. д.
Например, двоичное число 10111 может быть передано сигналами (импульсами) напряжения, показанными на рис. 16-11. Этот принцип и применяется в ЦВУ. Недостаток двоичной системы; в большом количестве разрядов счетчика по сравнению с системой десятичной, но он искупается большей простотой всего ЦВУ в целом. Перевод чисел из десятичной системы в двоичную и обратно производит само
ЦВУ.
Рис. 16-11. Передача двоичного числа серией импульсов.
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ В ДВОИЧНОЙ СИСТЕМЕ
Большое достоинство двоичной системы в простоте арифметических действий с числами, которые производятся так же, как и в десятичной системе. Сложим два числа, изображенные слева в десятичной системе, а справа — в двоичной..
В десятичной системе при сложении 5 + 9 единица (т. е. один десяток) переносится в старший разряд (десятков) и прибавляется к числам десятков 2 + 1. Точно так же и в двоичной системе: две единицы первого (правого) разряда дают двойку, которая, как единица, переходит в разряд двоек, а в сумме первого разряда получается нуль. Две единицы (двоек) второго разряда дают в сумме четверку, которая, как единица, переносится в разряд четверок. Сумма в разряде двоек равна нулю, а в разряде четверок — единице и т. д.
При вычитании в десятичной системе из разряда десятков пришлось занимать единицу и разность равна шести. При двоичной системе, в случае необходимости, из старшего разряда приходится занимать двойку, четверку и т. д. В первом разряде разность равна нулю. Во втором разряде из занятой двойки вычитается единица и в разности остается единица. В третьем разряде остается единица, а в четвертом и пятом нули.
В ЦВУ вычитание обычно заменяется сложением с числом, записанным обратным кодом, т. е. когда единицы числа заменены нулями,-а нули — единицами. При десятичной системе это делается так: уменьшаемое 25 складывается с числом, дополняющим вычитаемое до числа, выраженного единицей с нулями (100—19 = 81), и в сумме отбрасывают единицу высшего разряда. Ответ получается шесть, как и при вычитании.
В двоичной системе к числу 11001. прибавляется число 10011, записанное обратным кодом, т. е. число 01100. Далее, единица старшего разряда суммы переносится в младший разряд и прибавляется к нему. Ответ получается тот же, что и при вычитании. Все это выполняет самостоятельно арифметическое устройство ЦВУ. Таблица умножения в двоичной системе необычайно проста:
0.0 = 0; 1.0 = 0.1 = 0; 1.1 = l.
Таким образом, при умножении на единицу множимое число переписывается в соответствующий разряд, а при умножении на нуль производится сдвиг влево на один разряд. Все умножение сводится к сдвигу умножаемого числа на один разряд и сложению, что и выполняет арифметическое устройство.
Деление сводится к многократному вычитанию делителя из делимого и дополнению получаемого остатка справа
т. е. 56 : 8 = 7.
Так как умножение заменяется многократным сложением, деление — многократным вычитанием, а вычитание может быть заменено сложением, то все арифметические действия сводятся к сложению.
ПРИНЦИП РАБОТЫ НЕКОТОРЫХ ЭЛЕМЕНТОВ ЦВУ
Все ЦВУ состоит из устройств: запоминающего, управления, арифметического и др., а каждое из них из отдельных типовых элементов, называемых ячейками. Каждая ячейка выполняет определенные действия и, будучи включена определенным образом в общую схему, пропускает или задерживает посланный импульс усиливает его или сдвигает на разряд и т, д.
Данное состояние ячейки определяется высоким или низким уровнем напряжения, подаваемого на нее, наличием или отсутствием импульса напряжения или использованием импульсов двух полярностей. В ЦВУ используются приборы с односторонней проводимостью, электронные и полупроводниковые диоды и триоды.
Эти приборы в дальнейшем изображаются так, как показано на рис. 16-12. Прибор пропускает ток, когда потенциал анода выше потенциала катода (сопротивление прибора мало) и запирается при обратной полярности напряжения (сопротивление прибора очень большое).
а) Клапан или вентиль
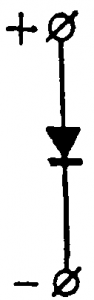Рис. 16-12. Условное изображение вентиля.
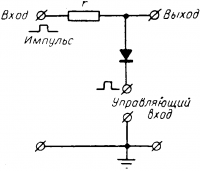
Клапан (вентиль) показан на рис. 16-13. Само название показывает, что он предназначен для задержки или пропуска импульса напряжения. Действительно, если на верхнюю точку входа подан прямоугольный импульс положительной полярности, то через вентиль пойдет ток от анода к катоду и через электрические цепи управляющего входа, не показанные на рисунке, к заземлению. Сопротивление rвелико, а сопротивление вентиля ничтожно и можно считать, что все напряжение падает на сопротивлении r. Следовательно, потенциал анода, а значит, и выход схемы почти не отличается от потенциала земли. Поэтому считают, что на выход импульс не передался (на выходе нуль). Если одновременно с импульсом на входе подать на управляющий вход положительный импульс такой же величины или большей, чем на входе, то вентиль запрется. Ток в сопротивлении r будет равен нулю,
а потенциал выхода равен потенциалу входа, т. е. положительный импульс передан на выход (единица). Этот механизм работы осуществляется во всех схемах с вентилями, приведенных ниже.
Рис. 16-13. Схема работы клапана.
б) Схема совпадения
Схема совпадения (условное обозначение И) показана на рис. 16-14. При появлении положительного импульса на анодах вентилей через них проходит ток. На сопротивлении r падает почти все напряжение и импульс на выход не передается (нуль). Если подать положительный импульс на один из входов A, Б и В, дело не меняется, так как ток будет проходить через два других вентиля. Положительный импульс (единица) передается на выход только в том случае, когда одновременно все три вентиля заперты положительными импульсами на управляющих входах A, Б и В почему и схема называется схемой совпадения.
в) Собирательная схема
Рис. 16-14. Логическая схема совпадения.
Собирательная схема (условное обозначение ИЛИ) показана на рис. 16-15. При подаче положительного импульса, хотя бы на один из входов А, Б, В, через сопротивление r будет протекать ток. Так как внутреннее сопротивление вентилей ничтожно, то все падение напряжения сосредоточено на сопротивлении r, а верхняя точка его и, значит, верхняя точка выхода будут точкой высокого потенциала (единица). Схема потому и называется собирательной, что собирает
импульсы (единицы), поступающие с разных направлений. Одновременно она при подаче положительного импульса на один из входов, например А, запирает высоким потенциалом два других входа Б и В.
г) Схема инвертора
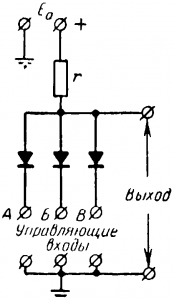Рис. 16-14. Логическая схема совпадения.
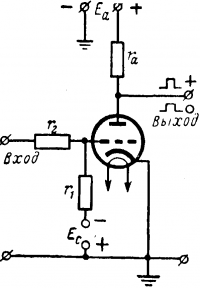
Схема инвертора (условное обозначение НЕ) показана на рис. 16-16. При отсутствии сигнала (нуль) на входе триод заперт отрицательным напряжением смещения Ес. Потенциал верхней точки выхода равен потенциалу положительного зажима источника анодного напряжения Еа, т. е. на выходе единица. При появлении положительного импульса на входе (сетке) триод проводит ток и напряжение нижней точки сопротивлений r, т. е, навходе резко падает (нуль). Таким образом, входной сигнал — единица преобразуется в сигнал — нуль.
Из схем основных схем формируются все более сложные схемы ЦВУ. В дальнейших схемах заземляющая их часть для простоты не показывается.
д) Цепочка клапанов
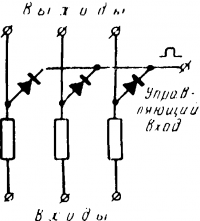
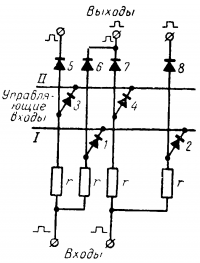
Цепочка клапанов с одним управляющим входом показана на рис. 16- 17. Импульсы с входов на выходы могут быть переданы только в том случае, когда на управляющий вход подан импульс, Запирающий вентили. Если этого импульса нет, то при положительных импульсах на входах через вентили проходит ток и благодаря большому падению напряжения на сопротивлениях r потенциал анодов и выходов близок к нулю.
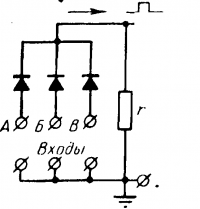
Рис. 16-15. Логическая схема собирательная.
е) Схема сдвигателя
Схема сдвигателя на один разряд дана на рис. 16-18. Как было показано выше, при умножении на единицу в двоичной системе само множимое число записывалось в соответствующий разряд, а при умножении на нуль это же число записывалось со сдвигом на один разряд. Операцию сдвига и выполняет сдвигатель.
Если высокий потенциал существует только на входах цифр, а на шинах I и II такого потенциала нет, то токи проходят через диоды 1,2,8,4и потенциалы на выходах очень малы (сигналов нет). При подаче положительного импульса на шину I запираются диоды 1 и 2; импульсы проходят через диоды 6 и 8 на средний и правый выходы. Диод 7 заперт высоким потенциалом левого входа. Если подать импульс на шину II, то запираются диоды 3 и 4. Через диоды 5 и 7 импульсы передаются на левый и средний выходы (сдвигаются влево), а диод 6 блокирован высоким потенциалом.
ж) Электронный триггер
Рис. 16-16. Логическая схема инвертора.
Электронный триггер или электронное реле является наиболее важным элементом ЦВУ. Он собирается из двух триодов или одного двойного триода, как показано на рис. 16-19. Особенность этого реле в том, что устойчивое состояние его будет только тогда, когда через одну половину лампы, например правую, ток проходит, а через другую — левую, нет, и наоборот.
Предположим невозможное, что через лампы Л1 и Л2 проходят равные токи. Пусть под влиянием ничтожнейшего, случайного изменения сопротивления в цепи лампы Л1 ток ее возрос. Тогда потенциал точки 1 уменьшится, ток делителя r5r6 уменьшится, потенциал точки 2, а значит, напряжение на сетке лампы Л2 упадет и ток в ее анодной цепи уменьшится. При этом увеличится потенциал точки 3, а следовательно, и напряжение на сетке лампы Лг. В результате этого ток в анодной цепи лампы Л1 лавинообразно нарастает, а лампы Л2 — падает. Таким образом, триггер за микросекунды приходит в такое состояние, когда лампа Л1 проводит ток (триод открыт), а лампа Л2 — заперта. Если подать положительный импульс на вход 2 или отрицательный на вход 1, то мгновенно лампа Л1запирается, а лампа Л2 — открывается.
Рис. 16-17. Цепочка клапанов с одним управляющим входом.
Схема триггера применяется в запоминающих устройствах и служит для запоминания только одного разряда числа.
Она может быть выполнена и на полупроводниковых триодах. Емкости, включенные параллельно сопротивлениям r3, r5 служат для ускорения переброса триггера, так как, представляя в этот момент очень малые сопротивления, они шунтируют большие сопротивления r3 и r5.
ПРИНЦИП РАБОТЫ ДВОИЧНОГО СЧЕТЧИКА
Как было сказано выше, триггер служит для запоминания одного разряда числа двоичной системы и фиксирует наличие цифры в разряде (единица) или отсутствие ее (нуль). Таким образом, количество триггеров равно количеству разрядов числа. Цепочка триггеров для запоминания одного числа называется регистром.
На рис. 16-20 показана схема работы двоичного счетчика на три разряда — три последовательно соединенные триггера. Пусть триггеры № 7, №2, №3, показанные в верхнем ряду, находятся в таком состоянии, когда проводит ток их левая часть (заштриховано) и не проводит — правая. Это состояние принято за нуль и число, записанное триггерами, 000. На вход триггера № 1 приходит серия равномерно следующих импульсов.
Рис. 16-18. Схема сдвигателя на один разряд.
Первый из них произведет переброс триггера в обратное состояние (1), что показано стрелкой → слева направо, на второй строке на рис. 16-20. На счетчике записано число 001. Второй импульс производит обратный переброс триггера № 1, справа налево, при котором проводит левая половина (0), но при этом перебросе триггер выдает свой импульс триггеру 2, в котором произойдет переброс слева направо. Таким образом, записано число 010.
При третьем импульсе на входе триггера № 1 происходит запись еще единицы —001; при четвертом прибавляется еще единица, а так как переброс был справа налево, то происходит передача импульса на триггер № 2. Переброс последнего был справа налево, следовательно, триггеру № 3 передается импульс уже с триггерами. Число, записанное на счетчике, равно 100, и т. д. Восьмой импульс произведет сброс всего числа. Таким образом, трехразрядный счетчик записывает числа от 0 до 7 десятичной системы.
ПРИНЦИП РАБОТЫ СУММАТОРА АРИФМЕТИЧЕСКОГО УСТРОЙСТВА
Предположим, что следует сложить два двоичных числа А = 1110 и Б = 1101. Сложение производится последовательно, разряд за разрядом, как при обычном счете.
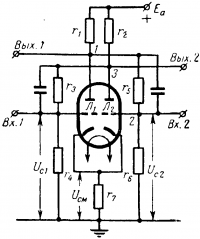Рис. 16-19. Схема триггера.
При сложении чисел первого разряда 0+1 в сумме получается 1; так же и при сложении чисел второго разряда 1 + 0 получается 1. При сложении чисел третьего разряда 1 +1 получается 2 . Следовательно, двойка, как единица, переносится в четвертый разряд или, как мы говорим, (единица вуме). Эта единица поставлена в строке переноса П, над числом А, Складывая четвертый разряд, получаем 3; половина двойки, т, в/1, идет и сумму С, а единица переноса переходит в сумму пятого разряда, где
С = П + А + Б = 1 + 0 + 0 = 1
Очевидно, устройство для суммирования — сумматор пpи последовательном суммировании, как это делалось, должен иметь два входа для чисел А и Б, вход для переноса П, выход для суммы С и выход для числа П, переносимого в следующий разряд. Блок-схема такого устройства, состоящего из запоминающего блока, однозарядного сумматора и устройства задержки (для переноса) на один разряд, показана на рис. 16-21.
Рис. 16-20. Работа двоичного счетчика.
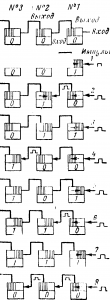Схема работы сумматора (рис. 16-22), осуществляется при помощи логических схем И, ИЛИ, НЕ. Для простоты все устройства заземления, формирования импульсов, усиления их на рис. 16-22 не показаны. При разборе схемы необходимо вспомнить следующее.
Так как все схемы И, кроме И1, присоединены к положительному зажиму источника энергии Еа, то через сопротивления r этих схем и внутреннее сопротивление источников сигналов проходит ток. Отрицательный зажим источников заземлен. Потенциал анодов этих схем невысок, так как значительная часть напряжения падает на сопротивлениях r. Импульсы высокого потенциала на анодах появляются только в те моменты, когда на все катоды приходят положительные импульсы напряжения, способные запереть вентили. Только тогда положительные импульсы схем И передаются дальше.
Через схемы ИЛИ положительный импульс проходит, если он подается хотя бы к одному аноду вентиля.
Схема НЕ заперта отрицательным потенциалом на сетке лампы. При этом потенциал ее анода высок, так как в ее анодном сопротивлении r ток не протекает. Этим потенциалом нормально заперт вентиль И1, и только в этом состоянии через его сопротивление г может пройти положительный импульс на выход С.
При появлении положительного импульса напряжения на сетке лампы она пропускает ток, потенциал на ее аноде падает и схема И1 открывается. В этом случае потенциал анода вентиля И1 при поступлении импульса от схемы ИЛИ1 будет низким, так как ток проходит через лампу схемы НЕ. Потенциал выхода С тоже, будет низким.
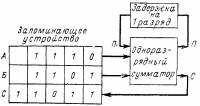Рис. 16-21. Блок-схема работы сумматора.
Теперь можно рассмотреть процесс сложения двух предложенных выше чисел. Триггеры регистра суммы С запоминающего устройства (рис. 16-21) перед началом операции сложения ставятся на нуль. Устройство управления посылает периодически импульсы, которыми и управляется схема. За каждый период складываются цифры одного разряда.
В течение первого импульса из запоминающего устройства (рис. 16-21) выбираются цифры младшего разряда А = 0 и Б = 1. Другими словами, на вход Б сумматора (рис. 16-22) поступает импульс положительного потенциала, а на входе А его нет. Тогда импульс проходит схему ИЛИ 1, сопротивление r схемы И 1, ИЛИ 2, на выход Сив младшем разряде регистра запоминающего устройства суммы С триггер перебрасывается в положения 1. Вторым импульсом из запоминающего устройства выбираются цифры А = 1 и 5 = 0. Импульс через вход (рис. 16-22) проходит схему ИЛИ 1, И1, ИЛИ2 и попадает на выход С. Триггер второго разряда запоминающего устройства перебрасывается в положение 1 (рис. 16-21).
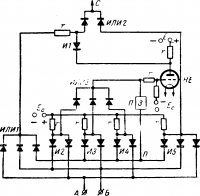Ряс. 16-22. Схема работы сумматора.
Третий импульс выбирает из запоминающего устройства цифры А = 1 и Б = 1 и на входе сумматора А, Б получаются положительные импульсы. Тогда запирается схема И2 и выдает положительный импульс на схему ИЛИ3. Импульс проходит на схему задержки Я и на сетку лампы схемы НЕ. Лампа отпирается и начинает проводить ток. Диод схемы И 1 отпирается, импульсы А и Б через схему ИЛИ 1 и схему И 1 проходят через лампу схемы НЕ. Потенциал анода схемы И1 низкий и на выход С через схему ИЛИ 2сигнал не поступает. Триггер третьего разряда С запоминающего устройства остается в положении 0.
Импульс напряжения на линии задержки задерживается до момента суммирования цифр четвертого разряда. Это равносильно тому, как человек держит единицу «в уме». Об устройстве линии задержки (З)будет сказано ниже.
В четвертый такт сложения, два импульса А, Б и импульс Я, выходящий из линии задержки, запирают схемы И2, И3, И4, которые через схему ИЛИ3 выдают второй импульс на схему задержки и схему НЕ. В этом случае, как уже указывалось, схемы ИЛИ 1 и И1 не выдают импульса на выход С. Однако поскольку схема И 5 заперта высоким потенциалом входа А, Б и первым импульсом схемы задержки П, то потенциал ее анодов становится высоким и через схему ИЛИ 2 на выход, в запоминающее устройство поступает импульс высокого напряжения. Происходит переброс триггера четвертого разряда в положение 1.
При пятом такте импульсы А, Б отсутствуют, но возникший импульс переноса при суммировании предыдущего разряда через линию задержки схемы ИЛИ 1, И 1, ИЛИ 2 выдается на выход С в пятый разряд сумматора. Триггер этого разряда записывает 1. Таким образом, просуммированы числа 1110 + 1101 = 11011 или в десятичной системе 14 + 13 = 27.
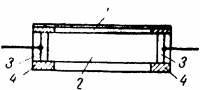На рис. 16-23 показан один из способов устройства линии задержки, Он основан на акустическом принципе. В стальную трубку 1, заполненную ртутью 2, вставлены две пластины из кварца 3, при помощи резиновых колец 4. Кварц имеет способность изменять свой объем при помещении его в изменяющееся электрическое поле. Если на вход одной пластинки подать импульс напряжения, то он вызовет механические колебания самого кварца и ртути в трубке, которые, с определенной скоростью, будут переданы другой кварцевой пластинке на выходе. Эти механические колебания кварц способен переобразовывать в электрические колебания на выходе. Скорость прохождения механических колебаний в ртути неизмеримо меньше скорости распространения электрических импульсов и поэтому электрический импульс передается с задержкой. Время задержки обычно составляет микросекунды. Меняя длину трубки, можно изменять время задержки.
Рис. 16-23. Устройство акустической линии задержки.
Статья на тему Двоичная система счисления
Двоичная система счисления
Однажды в Риме
Древних римлян часто поминают дурным словом за их громоздкую систему записи чисел. Люди не любят римские числа, так как они обременяют вычисления. Никто не обрадуется перспективе перемножать XLVII и DCDXXIV. А вот задача умножить 47 на 924 не выглядит настолько угрожающей (хотя большинство из нас все равно побежит за калькулятором). Впрочем, прежде чем сбрасывать римские числа со счетов как причудливый анахронизм, нам необходимо признать, что их основополагающий принцип – буквы вместо цифр – используется до сих пор. Этот ключевой аспект римских чисел обрел новое воплощение. Что легче прочесть?
• Реновация школ в нашем округе обойдется в 23000000 долларов
• Реновация школ в нашем округе обойдется в 23 млн долларов
Разумеется, я не стал разделять разряды в первом случае, чтобы число было сложнее прочесть (и я попал в точку, не правда ли?). Но, даже если проставить пробелы, фраза «Пентагон требует дополнительные 19 000 000 000 долларов» сложнее для восприятия, чем «Пентагон требует дополнительные 19 млрд долларов». Иногда удобнее использовать слова вместо чисел.
Мнимое преимущество позиционной системы счисления (это такая система счисления, в которой значение каждого символа в записи числа зависит от его позиции/разряда) – это то, что в ней проще производить вычисления. Но давайте задумаемся о том, сколько сил уходит на перемножение двух чисел. Во-первых, нам необходимо запоминать дополнительные математические данные. К тому же мы обязаны помнить таблицу умножения. Во-вторых, мы проделываем многоуровневую процедуру: сортируем числа по разрядам, умножаем по соответствующему правилу, получаем промежуточные данные, складываем.
Да, десятичные числа легче перемножать, чем их римские аналоги, однако это по-прежнему утомительно. Возникает вопрос, есть ли способ записывать числа, который бы облегчал вычисления. Мы выяснили, что да, есть, но для этого придется пожертвовать наглядностью.
Простейший способ записи чисел – единичная система счисления: мы просто записываем столько же символов (будем использовать цифру 1), сколько единиц в интересующем нас числе. Например, число 3 окажется трехзначным: 111. Сложение и умножение становятся исключительно простыми. Чтобы сложить 3 и 5, мы просто запишем два числа, 111 и 11111, друг за другом (без пробела) – и вот он, ответ: 11111111. Умножать тоже просто. Мы запишем одно число вертикально, а другое горизонтально и получим следующую таблицу:
Затем мы заполним таблицу, поставив единичку в каждом столбце и в каждой колонке:
Наконец, мы выпишем все единички в ряд и получим ответ: 111111111111111. Складывать и перемножать числа в единичной системе счисления существенно проще, чем десятичные или римские числа. Разумеется, такая простота вычислений дается ценой титанических затрат внимания и времени. Никому не захочется прибегать к этому методу, чтобы перемножить 47 и 924.Компромисс
Числа, записанные в двоичной системе счисления (система счисления с основанием 2), не так привычны нам, как десятичные или римские, но с ними проще делать вычисления. Вот почему в компьютерах используется именно двоичная система. Чтобы разобраться, как она устроена, нам нужно припомнить особенности десятичной системы.
Для записи чисел в десятичной системе счисления используют десять символов, располагаемых в разных комбинациях в ряд по горизонтали. Значение символа зависит от его места в ряду. 29 и 92 означают разные числа, потому что 2 и 9 занимают разные позиции. 29 означает «два десятка и девять единиц». 5804 означает «пять тысяч, восемь сотен, ни одного десятка и четыре единицы». Позиция цифры в десятичном числе означает, на какую степень десяти мы ее умножаем. Напомним, что показатель степени означает, сколько раз мы перемножаем основание: например, 10³ = 10 × 10 × 10. Естественно, 101 = 10. По договоренности, 100 = 1. Это логично, так как каждая следующая степень десяти в десять раз больше предыдущей. Разряды растут справа налево: единицы, десятки, сотни, тысячи, десятки тысяч и т. д. Иными словами, запись 5804 означает:
5 × 10³ + 8 × 10² + 0 × 101 + 4 × 100
1 × 2⁴ + 0 × 2³ + 1 × 2² + 1 × 21 + 0 × 20 = 16 + 4 + 2 = 22
Двоичные числа труднее для чтения, чем десятичные. Двоичная запись 1011001 кажется менее привычной, чем десятичная запись того же числа: 89. Преимущество двоичных чисел в том, что их использование облегчает вычисления. Вместо огромного количества математических данных нам необходимы всего две таблицы:
Заметьте, что в таблице умножения 10 означает число два. Сложение двоичных чисел устроено так же, как в десятичной системе. Например, нам нужно найти сумму 101002 и 11102. Расположим эти числа друг над другом:
Дальше нужно двигаться справа налево, складывая цифры в каждом столбце и при необходимости перемещая единицу на столбец влево. В нашем случае мы сложим два нуля и получим ноль:
Дальше идет столбец двоек. Мы складываем 1 и 0 (переносить ничего не требуется):
Дальше – столбец четверок. Мы складываем 1 и 1, получаем 10, пишем 0, держим 1 в уме и переносим на столбец влево:
Следующий столбец – восьмерки. Складываем 1 и 0 и 1, получаем 10, пишем 0 и держим 1 в уме:
Заканчиваем на столбце, означающем, сколько раз в числе встречается 16. Сложение дает 10, мы пишем 0 в текущем столбце и 1 в столбце с разрядом 32:
Мы обнаружили, что 10100 + 1110 = 100010.
Переведем это на язык десятичных чисел:
101002 = 20, 11102 = 14, 1000102 = 34.
Разумеется, 20 + 14 = 34.
Умножение в двоичной системе проще, чем в десятичной. Достаточно усвоить два принципа: сложение двоичных чисел (мы в нем только что разобрались) и умножение на степени двойки.
Умножение числа на 10 в десятичной системе не представляет сложности: мы просто добавляем цифру 0 справа: 23 × 10 = 230. Точно так же выглядит умножение на 2 в двоичной системе: 1101 × 10 = 11010. В случае десятичных чисел это очевидно, в случае двоичных 1101 означает:
1 × 8 + 1 × 4 + 0 × 2 + 1 × 1.
Умножение на 2:
1 × 16 + 1 × 8 + 0 × 4 + 1 × 2 + 0 × 1
Лишний ноль на конце дает 11010.
Умножение на 4, 8 и другие степени двойки тоже просто: например, умножение на 810 (10002) равнозначно приращению трех нулей с правой стороны числа. Итак, умножение превращается в игру «перемести-и-добавь-цифры». Проиллюстрируем это на примере умножения 11010 на 1011. Для начала запишем второе число так:
1011 = 1000 + 10 + 1.
Умножение на 11010 можно представить так:
11010 × 1011 = 11010 × (1000 + 10 + 1) = 11010 × 1000 + 11010 × 10 + 11010 × 1 = 11010000 + 110100 + 11010.
Удобнее умножать в столбик:
А вот и ответ:
Давайте переведем числа в десятичные, чтобы удостовериться, что все правильно:
110102 = 16 + 8 + 2 = 26;
10112 = 8 + 2 + 1 = 11;
1000111102 = 256 + 16 + 8 + 4 + 2 = 286.
Мы не ошиблись: 26 × 11 = 286.
В десятичной системе мы можем записывать не только целые числа. Если поставить в конце запятую, мы получим новые места для цифр: по мере движения вправо степени десяти будут все меньше. Например, 34,27 – это компактный способ записи такого выражения:
Двоичная система тоже позволяет записывать дробные значения. Каждую следующую цифру после запятой (в случае с двоичной системой неправильно говорить «десятичная запятая», лучше называть ее двоичной запятой, или запятой в позиционном представлении числа) мы умножаем на предыдущую степень двойки. Например, 101,0112 означает:
Непривычный способ записать одну вторую: 0,12! Есть и другие системы счисления, помимо десятичной, единичной и двоичной. Программисты нередко пользуются шестнадцатеричной системой счисления. В десятичной системе 10 цифр (от 0 до 9), в шестнадцатеричной нам нужно 16 разных символов, поэтому числа от 10 до 15 обозначают с помощью букв от A до F. В третичной системе мы пользуемся цифрами 0, 1 и 2, здесь все строится на степенях тройки. Скажем, 11023 означает:
1 × 27 + 1 × 9 + 0 × 3 + 2 × 1 = 38
В дробях первая позиция справа от запятой означает умножение на одну третью, вторая позиция – на одну девятую и т. д.:
Ответ на задачу
Если представить 42 в виде суммы степеней двойки, мы увидим, что это 1010102. А число 110112 можно представить как 16 + 8 + 2 + 1 = 27.
Двоичная система — это… Что такое Двоичная система?
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
- Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток — нет тока, индукция магнитного поля больше пороговой величины или нет и т. д.
- Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину индукции магнитного поля, потребуется ввести два пороговых значения, что не будет способствовать помехоустойчивости и надёжности хранения информации.
- Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
- Возможно применение аппарата алгебры логики для выполнения побитовых операций над числами.
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).
1 + 0 = 1 1 + 1 = 10 10 + 10 = 100
Таблица умножения двоичных чисел
0 • 0 = 0 0 • 1 = 0 1 • 0 = 0 1 • 1 = 1
Использование двоичной системы при измерении дюймами
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 715/16″, 311/32″ и т. д.
Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.
Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | ||||
| 32 | +16 | +2 | +1 |
Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо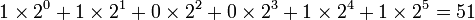 
.
Преобразование методом Горнера
Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.
Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа
Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.
unsigned int to_deg_2(unsigned int num){
int i;
if ( num == 1 ) return 2;
for( num-=1,i=1; i < sizeof(unsigned int)*8; i*=2 ) num = num|(num>>i);
return num+1;
}
Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
19 /2 = 9 с остатком 1 9 /2 = 4 c остатком 1 4 /2 = 2 с остатком 0 2 /2 = 1 с остатком 0 1 /2 = 0 с остатком 1
Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.
Другие системы счисления
В статье «Системы счисления (продолжение)»[1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.
См. также
Ссылки
- ↑ http://potan.livejournal.com/91399.html Системы счисления (продолжение)
Wikimedia Foundation. 2010.
Двоичная система счисления. Правила двоичной арифметики.
В двоичнойсистеме счисления для записи чисел используется две цифры 0 и 1. Основание системы q=2 записывается как 102= [1*21+0*20]10. В данной СС любое число может быть представлено последовательностью двоичных цифр. Эта запись соответствует сумме степеней цифры 2, взятых с указанными в ней коэффициентами: X=am×2m+am-1×2m-1+…+a1×21+a0×20+… . Например, двоичное число (10101101)2=1×27+0×26+1×25+0×24+1×23+1×22+0×21+1×20=17310.
Арифметические операции над двоичными числами отличаются простотой и легкостью технического выполнения.
Правила двоичной арифметики:
Сложение:0+0=0 1+0=1
0+1=1 1+1=10
— перенос единицы в старший разряд.
Вычитание:0-0=0 1-1=0
1-0=1 10-1=1
— заем единицы в старшем разряде.
Умножение:0х0=0 1х0=0
0х1=0 1х1=1
Двоичная система счисления является основной для использования в ЭВМ, удобной из-за простоты выполнения арифметических операций над двоичными числами. С точки зрения затрат оборудования на создание ЭВМ эта система уступает только троичной системе счисления.
В двоично-кодированных системах счисления, имеющих основанияq, отличные от 2 (q>2), каждая цифра числа представляется в двоичной системе счисления. Наибольшее применение в ЭВМ получили шестнадцатеричная система счисления и десятичная двоично-кодированная система счисления.
Восьмеричная и шестнадцатеричная системы счисления.
Восьмеричная и шестнадцатеричная системы счисления являются вспомогательными системами при подготовке задачи к решению. Удобство их использования состоит в том, что числа соответственно в 3 и 4 раза короче двоичной системы, а перевод в двоичную систему счисления и наоборот несложен и выполняется простым механическим способом.
Пример 2.1. Число 137,458 перевести в двоичную систему счисления. Перевод осуществляется заменой каждой восьмеричной цифры трехзначным двоичным числом (триадой):
1 | 3 | 7, | 4 | 5 |
001 | 011 | 111, | 100 | 101 |
т,е 137,458 = 001011111,1001012. И наоборот, заменой каждой триады слева и справа от запятой эквивалентным значением восьмеричной цифры образуется восьмеричное число.
Если в крайней слева или справа триаде окажется меньше трех двоичных чисел, то эти тройки дополняют нулями.
Пример 2.2. Число 5F,9416 перевести в двоичную систему счисления. Перевод осуществляется заменой каждой шестнадцатеричной цифры четырехзначным двоичным числом (тетрадой):
5 | F, | 9 | 4 |
0101 | 1111 | 1001 | 0100 |
т.e. 5F,9416=01011111,100101002. Число 5F,9416 в восьмеричной системе счисления имеет вид 137,458.
В десятичной двоично-кодированной системе счисления, часто называемой двоично-десятичной системой, используются десятичные числа. В ней каждую цифру десятичного числа (от 0 до 9) заменяют тетрадой.
Пример 2.3. Число 273,5910 перевести в двоично-десятичную систему счисления. Перевод осуществим следующим образом:
2 | 7 | 3, | 5 | 9 |
0010 | 0111 | 0011 | 0101 | 1001 |
т.е. 273,5910 = 001001110011,010110012-10
Двоично-десятичную запись числа используют непосредственно или как промежуточную форму записи между обычной десятичной его записью и машинной двоичной. Вычислительная машина сама по специальной программе переводит двоично-десятичные числа в двоичные и обратно.